基于线路电压稳定指标的连续潮流计算方法

周建方，何禹清，何红斌，李翠翠，李培强

（1.国网湖南省电力公司经济技术研究院，长沙 410004；2.湖南大学电气与信息工程学院，长沙 410082）

连续潮流CPF（continuation power flow）及其改进工具在电力系统静态稳定性分析和系统最大可用传输能力计算等方面得到了广泛的应用[1-7]。在CPF计算过程中，经常会遇到计算失败的情况，在这种情况下，无论如何缩小校正步长都不能得到潮流方程的解。该现象可能在解轨迹的鼻点附近出现，也可能在离鼻点较远的位置出现。如果在计算曲线的下半支出现计算发散问题，这对系统的稳定裕度及其他指标的计算没有影响，而仅仅是无法描述完整的PV曲线。但是如果发散出现在曲线的上半支，那么将无法得到确切的稳定裕度和鼻点位置，导致运行人员对系统的悲观估计，以致无法采取正确的应对策略。

目前，许多学者对CPF的计算失败问题提出了应对策略。文献[8]提出一种以线路无功损耗为参数化方程的CPF计算方法。文献[9]系统论证了CPF计算失败的两种现象，提出采用局部参数化方法取代弧长或拟弧长等全局性参数化方法来避免临界点失败，并采用参数受迫变换策略来克服非临界点失败。文献[10]在预测切向量规格化基础上，提出改进局部参数化方法的参数选择策略，以减少局部参数化方法在校正过程中不收敛的可能性。文献[11]提出一种节点类型扩展CPF模型，给出了新的节点类型双向转换逻辑和静态电压稳定临界点类型识别方法。文献[12]从预测算法和校正算法两方面改进，从而得到负荷裕度的近似值。文献[13]利用负荷裕度最大化的最优潮流计算结果来区分电压稳定极限点，并求出负荷裕度对控制变量的灵敏度，以实现电压稳定极限点的快速判定。文献[14]通过建立PQ-PV相互转换的方程组解决临界点附近的无解问题。

电压失稳具有很强的局部特性[15-18]，该特性贯穿CPF计算的整个过程，因此CPF参数化过程必须充分考虑电压稳定的局部特性。基于上述分析，本文提出一种以线路无功损耗为参数化方程的CPF改进算法，利用线路电压稳定性指标确定参数化线路的选取，并随着负荷的变化不断更新参数化线路，提出利用拓展潮流方程的预测方向向量的角度变化，对CPF的计算阶段进行判断，针对不同的计算阶段，自适应地选取步长控制策略。最后通过算例表明本文所提方法的有效性。

1 解决计算失败的策略

1.1 改进的参数化方法

以线路的无功功率损耗作为新的参数化方程，扩建的拓展潮流方程为

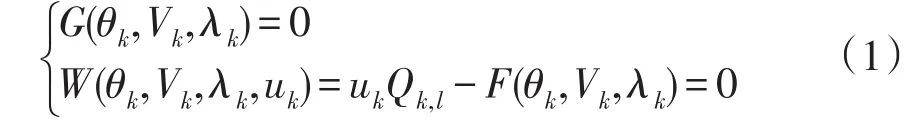
式中：Vk、θk分别为状态k下系统的各节点电压幅值和相角；λk为负荷增长因子；uk为状态k时的损耗因子；Qk,l为线路l在状态k时的无功损耗；函数G为常规有功潮流方程和无功潮流方程组成的潮流方程；函数F为线路l的无功损耗方程；函数W为以无功损耗方程为依据的参数化方程。

用牛顿-拉夫逊法求解拓展潮流方程，并确定下一个解的预测方向tk为

式中：Jk为状态k下的潮流方程的雅可比矩阵；J-1k为Jk的逆矩阵；Δuk为状态k时的损耗因子偏差，其值等于状态k时与状态k-1时损耗因子的差值。

1.2 参数化的线路的选择

对于图1所示的典型2节点电力系统等值电网，线路l首端节点i向线路l末端节点j传输的有功功率Pl和无功功率Ql可分别表示为

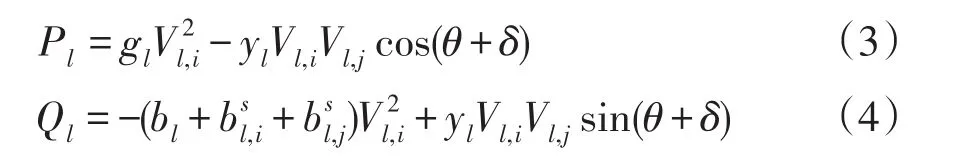
式中：gl、bl、yl分别为线路l的电导、电纳、导纳；分别为线路l的节点i、j安装的无功补偿设备对应的电纳值；Pl、Ql分别为线路l的有功功率和无功功率；Vl,i、Vl,j分别为线路l首端节点i、末端节点j的电压幅值；θ为线路阻抗角；δ为首末两端的电压相角差。

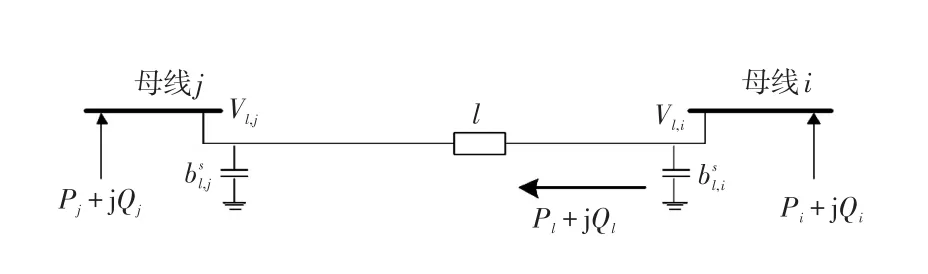
图1 DG站址和容量安排Fig.1 Arrangement of locations and capacities of DGs

式（3）和式（4）可改为

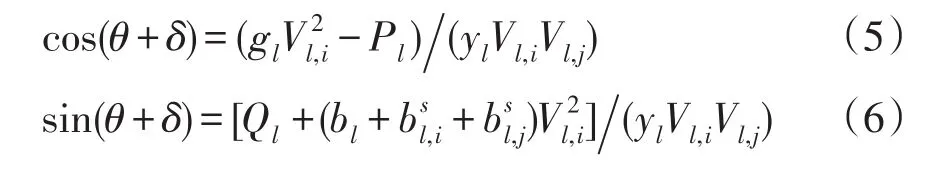
将式（5）和式（6）中的θ、δ消去得到

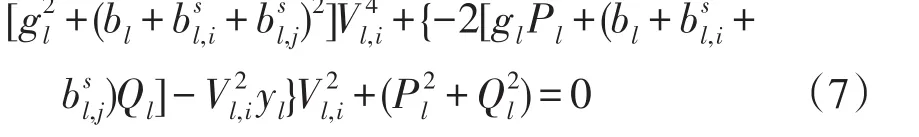
为保证电网的电压稳定，关于式（7）的一元方程必须要有实数解，即方程式的根判别式应大于或等于0，根据此原理化简后可以得出线路l的线路电压稳定指标Ll为

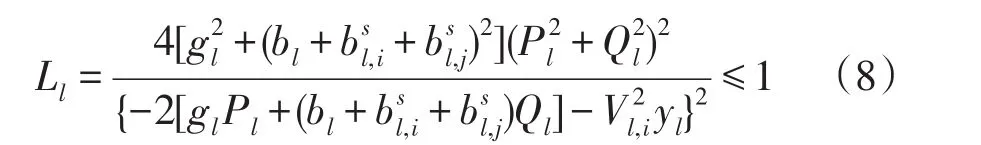
从式（8）可以看出，Ll可表示线路的电压稳定性情况，Ll值越小则此线路越稳定，Ll值越接近1则此线路越不稳定。

线路的无功损耗值与系统负荷基本呈线性关系，然而某些线路特别是补偿较充分线路的无功损耗值可能不随负荷的增大而增大。因此寻找一种方案能自动转换所选线路，选择负荷变化前后电压幅值变化最大的节点，如果此节点与多条支路相连，计算各支路的稳定性指标Lij，选择稳定指标值最小的线路作为参数化方程的线路。

2 步长调整策略

CPF计算过程中，状态点越接近鼻点位置，其前后两次的预测方向夹角越大，因此可利用前后两次预测方向夹角的余弦值cos tk,tk-1来对CPF的计算阶段进行判断，如图2所示。若k=1，则表明计算处于开始阶段，当前系统远未到达系统拐点，更新计算阶段标志 Sk+1=1；若 k＞1且0≤cos tk,tk-1≤α，则表明当前系统还未到达系统拐点，更新计算阶段标志 Sk+1=1；若 k＞1且cos tk,tk-1＜0或cos tk,tk-1＞α，则表明当前系统已到达系统拐点，更新计算阶段标志Sk+1=0，即

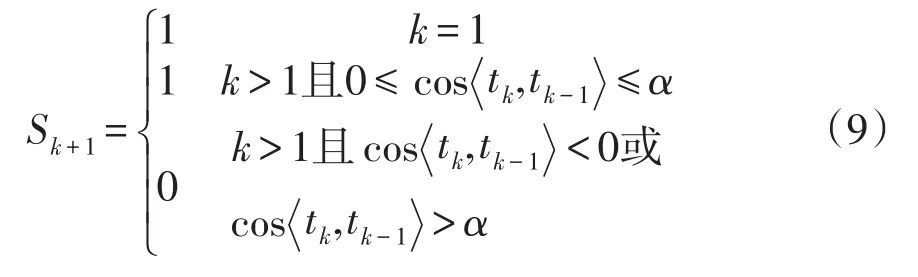
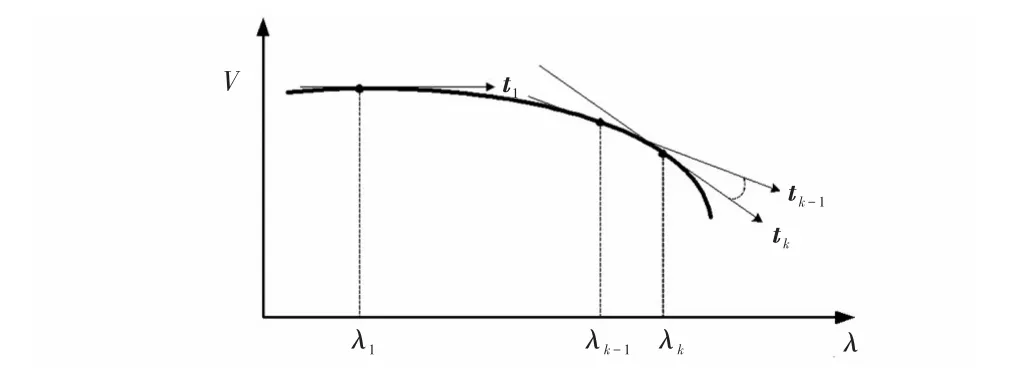
图2 CPF计算阶段判断示意Fig.2 Schematic of judgement on the calculation stage of CPF

利用预测方向tk，计算步长σk+1为

式中，‖tk‖为预测方向tk的欧几里得范数。

若计算阶段标志Sk+1=1，则更新步长σk+1=（σk+1+σk）2；若计算阶段标志 Sk+1=0，不更新步长，可表示为

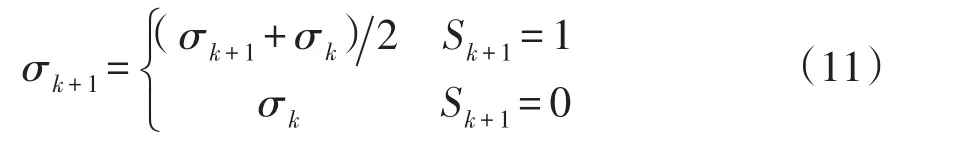
3 算法流程

计算流程如图3所示，计算步骤如下：

步骤1 读取潮流计算基础数据并形成系统网络阻抗矩阵，设定初始状态k=1，初始计算阶段标志S1=1，初始步长σ1=1，损耗因子u1=1；

步骤2 执行潮流计算，求出各负荷节点的电压、相角相量和各线路的功率相量；

步骤5 用牛顿-拉夫逊法求解拓展潮流方程，并确定下一个解的预测方向tk；

步骤6 利用前后两次的预测方向夹角的余弦值对CPF的计算阶段进行判断；

步骤7 利用预测方向tk，计算步长σk+1；

步骤8 确定下一个解的预测值；

步骤9 采用常规CPF校正法，对上述扩展CPF方程进行求解，如果潮流收敛，设置k=k+1，并返回步骤3；否则，若计算阶段标志Sk+1=1，则更新步长为（σk+1+σk）2，并返回步骤8；若计算阶段标志Sk+1=0，则不更新步长，直接输出结果，计算结束。

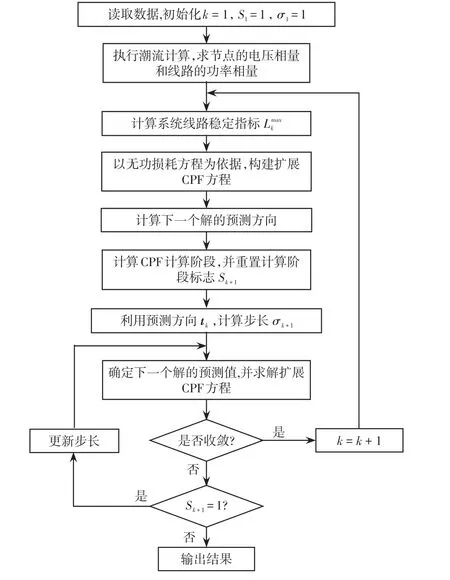
图3 计算流程Fig.3 Flow chart of calculation

4 算例分析

对如图4所示的IEEE14节点系统[13]进行仿真计算，取α=0.5。

图5为利用本文方法计算得到的PV曲线，从图5中可以看出，本文方法仅通过7个状态点就到达拐点位置，计算速度快，在状态k=8时，计算阶段标志Sk+1=0，表明系统已到达系统拐点。同时，线路电压稳定特征指标=0.932，接近1且远大于初始状态点的0.547和前点的0.798，表明系统中已有线路处于不稳定状态。因此，计算阶段标志值和线路电压稳定特征指标值两个重要指标能够有效判断系统是否处于极限运行状态。

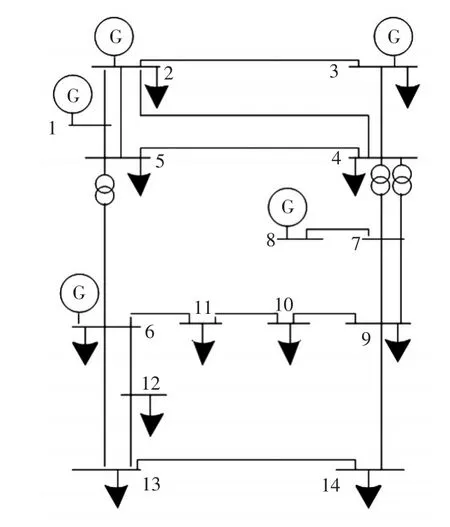
图4 IEEE14节点系统Fig.4 IEEE 14-node system

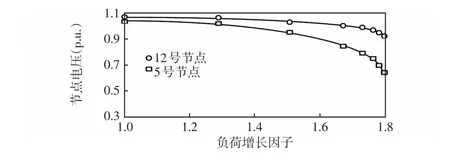
图5 IEEE14节点系统的PV曲线Fig.5 PV curves of IEEE 14-node system

图6为各状态点线路电压稳定特征指标对应的线路标号。从图6中可以看出，本方法所提的线路电压稳定特征指标对应的线路在各状态点并非一成不变，线路电压稳定特征指标对应的线路会随着系统最不稳定区域的变化而变换。在状态k=3时，系统整体处于稳定状态，但线路12受潮流分布影响，其无功损耗增量较上一状态明显增大，其对应的线路电压稳定指标最大，若该节点两端电压差继续增大将出现失稳。因此，该指标能体现电压失稳的局部特性，以及反映系统的弱节点和弱区域。

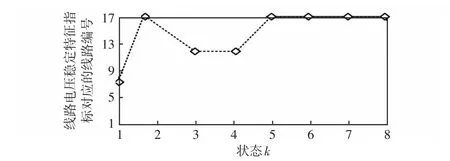
图6 各状态点线路电压稳定特征指标对应的线路标号Fig.6 Line labels of line voltage stability characteristic indexes at each state point

表1为各状态下CPF计算迭代次数，可以看出本文方法所需的迭代次数少，计算收敛速度快。

表1 各状态点的CPF计算迭代次数Tab.1 Number of iterations at each state point in the calculation of CPF

图7为各状态点的计算阶段标志值，计算阶段标志值在状态k=8之前均为1，只有到状态k=8时才更新为0，说明本文方法所提的计算阶段判断方法能准确判断CPF的计算阶段。

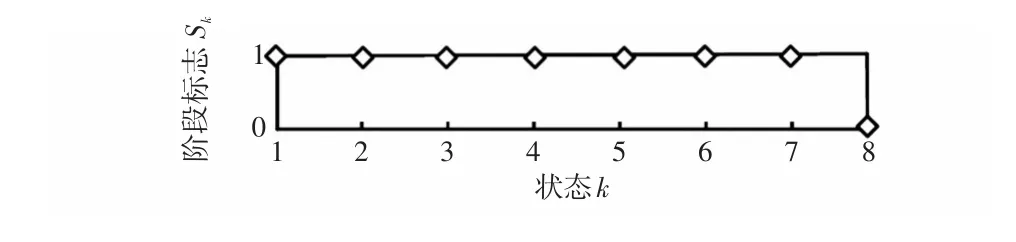
图7 各状态点的计算阶段标志值Fig.7 Stage flag at each state point on the calculation stage

图8为各状态点的步长更新次数。从图8中可以看出，在状态k=5之前，系统状态变化平缓，步长未进行更新便能实现潮流校正的收敛；在状态k=5之后且k=8之前，系统状态临近拐点位置，大步长无法保证潮流校正的收敛性，启动步长自适应调整策略；在状态k=8时，虽然大步长已无法保证潮流校正的收敛性，但此时计算阶段标志值已更新为0，系统已到达系统拐点，无需再进行步长调整来实现潮流校正的收敛。因此，本文方法所提出的步长控制策略能有效地结合计算阶段标志实现自适应调整。

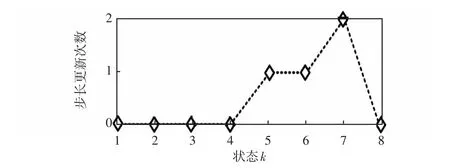
图8 各状态点的步长更新次数Fig.8 Number of step size updates at each state point

运用本文方法对湖南省2015年110 kV以上规划主网架进行电压稳定裕度（PV曲线计算）分析，纳入电压稳定裕度分析的变电站共795座，其中500 kV变电站10座，220 kV变电站139座，110 kV变电站646座。表2为本文方法与PSASP程序的正交平面法、BPA软件的弧长法等计算性能对比。本文方法能依据线路电压稳定指标识别系统是否接近临界点区域，并依据其状态对步长和下一预估状态点进行实时调整，避免了正交平面法、弧长法等全局性参数化方法在临界点区域步长和方向的无效预估，造成潮流无解。本文方法计算成功率分别高出正交平面法和弧长法2.48和2.17个百分点，PV曲线完整率分别高出3.57和3.88个百分点，同时，平均计算时间仅为正交平面法的76.68%和弧长法的76.10%，计算速度明显加快。

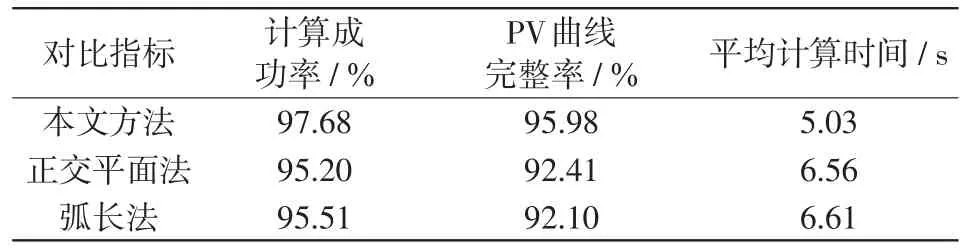
表2 不同方法计算性能对比Tab.2 Comparison of calculation performance using different methods

5 结论

（1）本文方法以线路电压稳定指标为依据，选择线路的无功功率损耗作为新的参数化方程，构建扩展CPF方程，能体现电压失稳的局部特性，反映系统的弱节点和弱区域。

（2）本文方法利用拓展潮流方程的预测方向向量的角度变化，对CPF的计算阶段进行判断，并以此为基础，对CPF计算过程中的步长进行控制，有效避免了计算的不收敛。

（3）IEEE14节点算例及在湖南省电网的计算表明本文所提方法的能有效、快速、较完整地计算得到PV曲线，在对大规模电网进行电压稳定裕度分析具有一定优势。