例谈“学为中心”下章节复习课设计意图的把握
张建云
(新昌县实验中学,浙江 新昌)
每当一章新课结束,我们都会碰到章节复习课,对一章节的知识进行梳理、巩固提升。而对复习课设计意图的把握很大程度上决定着复习课的效果。相对于新课教学有明确的课标要求,重点难点作为参考,设计时相对容易把握,而复习课内容宽泛,又没有相应的课标要求,全凭自身的理解去设计,所以不容易把握。
对于现在复习课的常态来说,往往以程序化的复习设计为主,即先复习知识然后讲解例题的模式。例题的安排也遵循由浅入深的设计方法,但由于设计时意图把握不够准确,存在选题不够恰当,或选题零乱缺少行进主线,对例题分析、把握不到位等现象。造成此等情况的主要原因是老师在设计时,没有兼顾学生的学习主线,没有在“学为中心”的原则下设计章节复习课,从而使课堂复习不够高效。下面我以《全等三角形的复习》举例阐述。
一、设计意图把握不当的几个现象
1.选题不够恰当
如:在全等三角形中,常会看到如下一题:
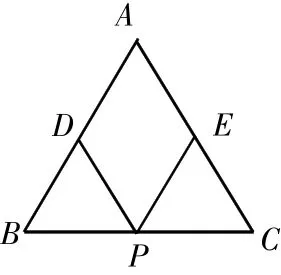
如图:在△ABC中,AB=AC=10 cm,D为AB中点,如果P在线段BC上由点B出发向C运动,同时E在线段上由点C向A运动。设运动时间为t(s)
(1)若点P的速度为3 cm/s,则t(s)时,BP=_____。若点E的运动速度与点P的运动速度相等,经过几秒时,△BPD与△CEP全等,并说明理由。角形的知识方法联系不大,放在全等三角形的章节复习中并不是最需要、最恰当的。
2.缺少行进主线
在构思设计时,需要把所选的习题串珠成线,使课堂有一个行进主线,逐步展开,避免课堂复习“东一榔头西一棒”,零乱而无序。而设计时若能有一个行进主线,无论是习题精选,还是内容重组、习题改编等,都围绕此主线去设计、编排,从而使课堂像慢慢展开的画卷一样,有序而有新意。如全等三角形属于图形变换,可设计以图形变换为主线,给出问题情景,不断推进呈现。如下图:
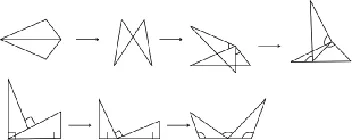
3.例题分析不到位
例题承载着相应的知识、方法、思想。如何去分析例题,挖掘出题目背后所蕴含的方法、技能,从而提升学生的数学能力,对于复习课尤为重要。
如本人听过一节《全等三角形复习》的公开课,对于其中一题课堂处理如下:
(2)若点E的运动速度比点P的速度慢1 cm/s,则点P的运动速度为多少时,△BPD与△CEP全等,请直接写出答案。
这题无疑是老师心目中的“好题”,但这题只是以全等为“外壳”,真正考查的是分类思想、方程思想、数形结合思想,与全等三
例题:如图 AC=BD,CD=AB,求证:∠B=∠C。
老师呈现题目后,叫学生回答,学生回答连接AD,说明△ACD与△DBA全等,然后就马上转入下一例题,这样的处理,就没有充分挖掘出此题目所蕴含的方法、技能,没有体现出这个例题最大的价值,学生的能力也不能得到提升。
二、如何把握章节复习课的设计意图
出现以上的问题,在于设计时没有把握住核心知识和核心技能,导致失之偏颇。那如何才能把握住核心知识和核心技能呢?我认为可以从以下几个方面入手。
1.设计前构建思维导图
在进行章节复习设计、确定核心知识时,不妨先对章节知识进行知识梳理。构建思维导图,使自己对本章知识有一个整体认识,便于找到知识主线(核心知识)、方法主线(核心技能)。如《全等三角形的章节》可构建如下思维导图。
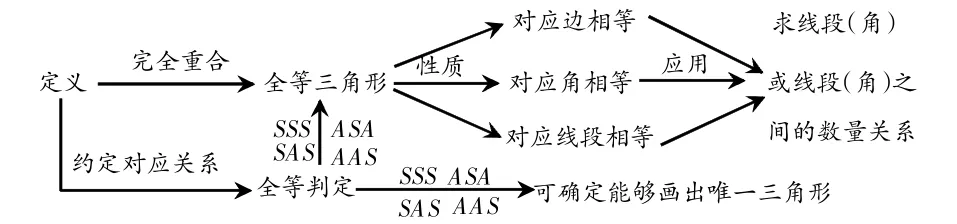
通过构建思维导图,更能帮助自己把握全章的核心知识、核心技能。
2.在整个教材中审视章节复习
站得高,才能看得远,才能把握住主线和核心,章节复习也是如此。在章节设计时,不能局限于这一章节,而应该结合课标,高屋建瓴,在整个教材体系中审视这一章节的地位和作用,以此来确定核心知识和核心技能。
如:全等三角形这一章节,就整个初中几何体系来看,它是研究几何图形的一个重要工具。在今后特殊三角形、四边形、相似三角形甚至圆中的研究,都是一个重要的方法(手段)。因此,能够熟练地寻找、预判、证明,甚至是创造全等三角形是今后几何学习的一项重要技能。因此,可以明确此为章节复习的核心知识、核心技能。
3.多审视习题背后的价值
确定核心知识、核心技能后需要围绕核心知识、技能去精选习题,甚至是重组、改编习题。本人认为一线教师能够根据需要去重组、改编习题固然最好,但很多时候却没有这样的心力和能力。现在能见到的习题资料繁多,若能有一双“慧眼”,多审视习题背后的作用和价值,就能精选出适合的“好题”。然后围绕习题精心设计问题串,以促使学生理解和把握核心知识和核心方法,而不是就题论题,浮于表面,使学生无所收获。
如:上面提到的一例题:
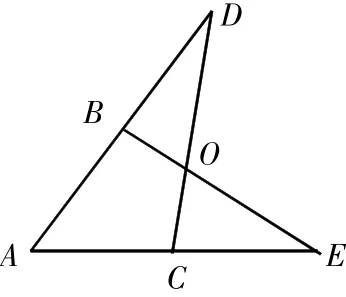
如图:AC=BD,CD=AB,求证:∠B=∠C。
它背后的价值在于让学生体会如何去寻找、发现,甚至创造全等三角形这一核心方法,也是今后几何研究中“三角形奠基法”这一思想的体现,是一道复习课的“好题”。可惜设计者没有关注它背后所体现的思想、方法,而是就题论题,一滑而过。可以考虑如下再设计:
师:呈现题目。
生:学生回答。
师:追问:为什么会想到连接AD,考虑△ACD≌△DBA,而不是△ACO≌△BOD?据此提出连接BC是否可行?让学生尝试证明。
生:完成证明过程。
师:再引导学生总结,如何去寻找,发现目标三角形?有什么方法?
即:可把AC=BD与CD=AB两两互相组合考虑,若AC=CD组合,可考虑△ACD,若AC与AB组合,可考虑△ABC,从而想到了连接AD或BC。这样学生就对这两条辅助线有一种豁然开朗之感。
师:然后再继续追问,能否把条件和所证结论组合,寻找目标三角形?
生:学生回答。
增加学生对此方法进一步的理解和把握。
师:最后给出变式练习题,进行巩固。
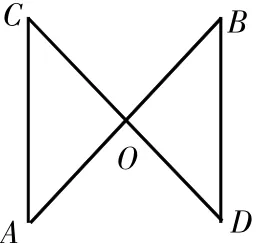
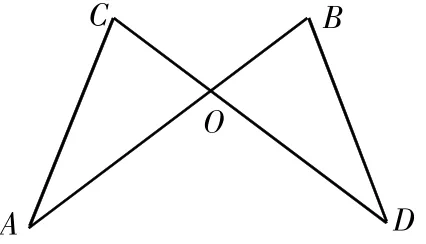
如图:△ABE的边BE和△ACD的边相交于点O,若AB=AC,BO=CO,求证:BD=CE。
这样的设计,充分发挥了例题的作用,通过复习不单巩固了知识,更重要的是提升了对核心方法和核心技能的理解。同时也能为后续几何学习奠定一个好的基础。
通过以上三个方面,能在章节复习设计中,把握住核心知识和核心技能。能在“学为中心”的教学理念下,注重思维的引导和点拨,注重学生对思路和方法的自主归纳和总结,注重课堂中先练后讲、合作学习等多种方式,突出学生的参与度,从而使复习课的设计更合理,课堂复习更高效。

