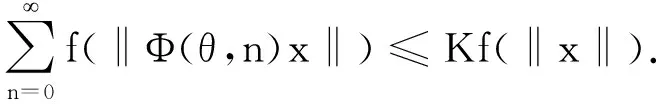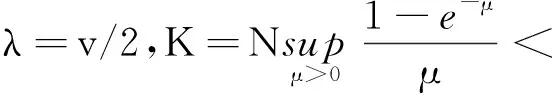线性斜积半流的一致指数稳定性的若干刻画
岳田,宋晓秋
(1. 湖北汽车工业学院 理学院, 湖北 十堰 442002; 2. 中国矿业大学 数学学院, 江苏 徐州 221116)
近年来,关于有限或无限维Banach空间中演化方程解的渐近行为研究取得了突破性进展,尤其在指数稳定性理论方面,取得了丰富的研究成果[1-14]. 由于在物理学、工程学、经济学中很难找到准确的数学模型去刻画动力系统,而其演化过程的解可以形成一个线性斜积半流,故可借助线性斜积半流来讨论该类发展方程的指数渐近行为.关于线性斜积半流的指数稳定性,MEGAN等利用容许性方法、Datko方法和构造函数空间上的泛函方法对其进行了相关讨论[3-7];文献[10-14]对斜演化半流的指数稳定性进行了探讨,从而推广了线性斜积半流的概念.本文将在上述文献的基础上,对Banach空间中线性斜积半流的一致指数稳定性给出Datko、Rolewicz型刻画及遍历刻画.
第1节给出后文需要的概念;第2节讨论线性斜积半流的一致指数稳定性,并给出了若干一致指数稳定的充分或必要条件,所得结果推广了稳定性理论中的一些经典结论.
1 预备知识
设X是一个Banach空间,(Θ,d)为一个度量空间,将空间X上的范数及其作用于有界线性算子全体B(X)上的范数记作‖·‖,I为恒等算子.
定义1[5]如果满足性质:
(i)σ(θ,0)=θ, ∀θ∈Θ;
(ii)σ(θ,t+s)=σ(σ(θ,s),t), ∀(θ,s,t)∈
则称连续映射σ:Θ×R+→Θ为Θ上的半流.
定义2[5]如果σ为Θ上的半流且Φ:Θ×R+→B(X)满足以下条件:
(i)Φ(θ,0)=I, ∀θ∈Θ;
(ii)Φ(θ,t+s)=Φ(σ(θ,t),s)Φ(θ,t),
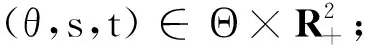
(iii)存在M≥1和ω>0使得
‖Φ(θ,t)‖≤Meωt,∀(θ,t)∈Θ×R+;
(iv)对所有的(θ,x)∈Θ×X,映射R+t|→Φ(θ,t)x∈X连续,
则称π=(Φ,σ)为X×Θ上的线性斜积半流.
例1设σ为度量空间Θ上的半流,X是一个Banach空间,A:Θ→B(X)为连续映射.若Φ(θ,t)x为抽象Cauchy问题:
的解,则π=(Φ,σ)为X×Θ上的线性斜积半流.
定义3如果存在常数N>0和v>0,使得对
∀(t,θ,x)∈R+×Θ×X,有
‖Φ(θ,t)x‖≤Ne-vt‖x‖,
(1)
则称线性斜积半流π=(Φ,σ)为一致指数稳定的.
2 主要结论及其证明
定理1线性斜积半流π=(Φ,σ)是一致指数稳定的当且仅当存在h>0和c∈(0,1),使得对每个θ∈Θ和每个x∈X存在τ∈(0,h],满足
‖Φ(θ,τ)x‖≤c‖x‖.
(2)
证明必要性显然. 下证充分性.
设任一固定的θ∈Θ,x∈X. 由假设知,存在τ1∈(0,h],使得式(2)成立. 对θ1=σ(θ,τ1)和x1=Φ(θ,τ1)x可选择τ2∈(0,h],使得
‖Φ(θ1,τ2)x1‖≤c‖x1‖≤c2‖x‖,
由于
Φ(θ1,τ2)x1=Φ(σ(θ,τ1),τ2)Φ(θ,τ1)x=
Φ(θ,τ1+τ2)x,

由数学归纳法得
‖Φ(θ,sn)x‖≤cn‖x‖,n∈N.
(3)
若sn→(n→),则对每个t∈[sn,sn+1],有t≤(n+1)h. 从而
‖Φ(θ,t)x‖= ‖Φ(σ(θ,sn),t-sn)Φ(θ,sn)x‖≤
Meωhcn‖x‖≤Me(ω+v)he-vt‖x‖,
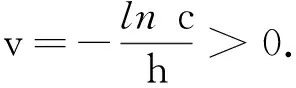
如果sn→s(n→),利用式(3)可得Φ(θ,s)x=0. 当t≥s时,
Φ(θ,t)x=Φ(σ(θ,s),t-s)Φ(θ,s)x=0,
当0≤t 综上可知,对∀(t,θ,x)∈R+×Θ×X,式(1)成立. 证毕! 定理2如果φ,ψ: [0,)→[0,)是2个非减的函数,满足,且对所有(θ,x)∈Θ×X,有 (4) 则线性斜积半流π=(Φ,σ)是一致指数稳定的. 证明结合已知条件,利用反证法推出式(2)成立. 如果式(2)不成立,则对每个h>0及每个c∈(0,1)存在x0∈X,‖x0‖=1及θ0∈Θ,使得 ‖Φ(θ0,τ)x0‖>c‖x0‖=c 对所有τ∈(0,h]成立. 从而由式(4)可得,对所有h>0,有 因此,由L’Hospital法则,有 此矛盾说明式(2)成立. 从而π=(Φ,σ)是一致指数稳定的. 证毕! 推论1若φ(t)满足定理2的条件,则线性斜积半流π=(Φ,σ)是一致指数稳定的当且仅当存在2个常数α>0和β>0使得对所有的(θ,x)∈Θ×X有 (5) 证明必要性. 设存在常数N>0,v>0,使得‖Φ(θ,t)‖≤Ne-v t对所有t≥0和θ∈Θ成立,任意固定的α∈(0,v]及β≥N,对每个θ∈Θ和每个x∈X,当t>0时,有 由定理2可知充分性显然. 证毕! 推论2如果φ(t)满足定理2的条件,且存在3个常数α>0,β>0,γ>0,使得对所有的(θ,x)∈Θ×X,有 (6) 则线性斜积半流π=(Φ,σ)是一致指数稳定的. 证明利用式(6),当t>0时有 其中γ=Meω+α,M,ω由定义2给出. 进而由推论1可知结论成立. 证毕! 定理3线性斜积半流π=(Φ,σ)是一致指数稳定的当且仅当存在非减函数f(t)>0(t>0)满足f(ts)≤f(t)f(s) (t,s≥0)及K>0,使得对所有x∈X和θ∈Θ,有 (7) 证明必要性. 若π=(Φ,σ)是一致指数稳定的,则存在常数N>0,v>0,使得对所有x∈X和θ∈Θ,有 因此,当f(t)=t,K=N/v时,式(7)成立. 充分性. 如果π=(Φ,σ)非一致指数稳定,则对每个h>0及每个c∈(0,1),存在x0∈X及θ0∈Θ,使得对所有τ∈(0,h],有 ‖Φ(θ0,τ)x0‖>c‖x0‖, (8) 特别地,取h=Kf(3)及c=1/3,由式(8)有 与式(7)矛盾. 因此,π=(Φ,σ)是一致指数稳定的. 证毕! 定理4线性斜积半流π=(Φ,σ)是一致指数稳定的当且仅当存在非减函数f(t)>0(t>0),满足f(ts)≥f(t)f(s) (t,s≥0)及K>0,使得对所有x∈X和θ∈Θ, 式(7)成立. 证明必要性. 令f(t)=t即可证得必要性. 充分性. 类似定理3. 由式(8),对c∈(0,1)和h=K/f(c),有 与式(7)矛盾. 因此,π=(Φ,σ)是一致指数稳定的. 证毕! 推论3线性斜积半流π=(Φ,σ)是一致指数稳定的当且仅当存在p>0及K>0对所有x∈X和θ∈Θ,有 (9) 推论4若f(t)满足定理3或定理4的条件,则线性斜积半流π=(Φ,σ)是一致指数稳定的充要条件为存在K>0对所有x∈X和θ∈Θ,有 (10) 定理5线性斜积半流π=(Φ,σ)是一致指数稳定的当且仅当存在K>0,λ>0对所有t>0及∀(θ,x)∈Θ×X,有 (11) 证明必要性. 如果π=(Φ,σ)是一致指数稳定的,则由定义,存在N>0,v>0,使得对∀(θ,x)∈Θ×X,有 充分性. 类似定理3的证明. 如果π=(Φ,σ)不是一致指数稳定的,设h>0满足eλh>1+3λhK,其中K,λ由式(11)给出,由定理1知,当c=1/3时存在x0∈X及θ0∈Θ对所有τ∈(0,h],有式(8)成立. 从而当t=h时,有 与式(11)矛盾,因此π=(Φ,σ)是一致指数稳定的. 证毕!