基于EMD和ARMA模型的上证指数预测①
吴振宇 喻敏 金吉 姜楠
摘 要:针对上证指数具有非线性、非平稳性的特点,研究了一种基于经验模态分解(EMD)和自回归滑动平均模型(ARMA)的预测方法。首先利用EMD对上证指数数据进行平稳化处理,使上证指数数据更有规律性,改善上证指数数据的非线性、非平稳性特性,然后利用ARMA模型对分解后的数据建模预测。研究结果表明:和直接利用ARMA模型进行预测所得的结果相比,本文所提的方法预测精度更高。
关键词:经验模态分解(EMD) 自回归滑动平均模型(ARMA) 上证指数 预测
中图分类号:F832.51 文献标识码:A 文章编号:2096-0298(2018)06(a)-033-03
股市一直以来受诸多因素的影响,导致股市变化莫测,股票具有高风险、高回报的特点,有效的股市上证指数预测研究是降低风险,提高获利的关键[1~2]。目前常用的股票预测研究方法包括:支持向量机法[3~4]、卡尔曼滤波法[5]、神经网络方法[6~7]等。卡尔曼滤波法是将股票数据作为状态变量建立状态空间模型,该方法更加适用于对股票数据的在线预测,但难以估计噪声的统计特性。支持向量机在处理小样本方面有较大优势,但一些参数的选择将直接决定预测的精度,目前支持向量机仍然缺乏公认有效的参数选择方法。神经网络法具有较强的泛化能力,但神经网络法容易在局部最小点出现错误,从而导致产生的预测结果不够稳定。由于ARMA模型在建模时能将影响股票的因素综合起来[8],本文选取ARMA模型来预测上证指数,由于ARMA模型用于处理平稳序列,针对上证指数数据具有非线性、非平稳性的特点,需要先对其进行平稳化处理。对数据进行平稳化处理的方法主要有小波变换和经验模态分解(EMD)方法。由于EMD在提取趋势项上更有优势[9],因此本文选用EMD对上证指数数据进行平稳化。
针对上证指数数据非线性、非平稳性的特点,本文采用EMD和ARMA模型的组合方法来预测上证指数数据,本文选取网易财经自2014年3月26日至2016年11月26日期間的每日收盘价上证指数进行建模预测,首先利用EMD方法分解上证指数数据,获得若干个分解的子序列,由于这些子序列能体现原始信号的不同尺度波动成分,因此使得分解后的数据比原始数据更加平稳,再用ARMA模型对每个子序列进行建模预测,最后将所有子序列的预测结果相加就得到了对原始上证指数数据的预测。
1 算法原理
1.1 EMD算法
经验模态分解[10](Empirical Mode Decomposition,EMD)方法的基本原理是将信号中不同特征尺度或趋势逐级分解进而产生有限个固有模态函数(IMF),分解后的IMF分量体现了原始信号的不同尺度波动成分,因此EMD是一种有效的处理非线性信号的方法。其分解的具体过程为。
设待分解的信号为,对其进行EMD的具体步骤为:
(1)确定出信号的所有极大值和极小值。
其中,为随机过程。
ARMA模型的定阶也可以通过AIC准则来确定,其原理为:选取不同的p、q对时间序列进行拟合,计算出相应的AIC值。当AIC值达到最小值的模型就是最佳模型,AIC准则是衡量统计模型拟合优良性的一种标准,它可以用来权衡所估计模型的复杂度和此模型拟合数据的优良性。
2 实例分析与论证
2.1 股票数据采样与处理
为验证本文所提方法的有效性,选取网易财经2014年3月至2016年11月每隔一天测量的1000个收盘价上证指数进行建模预测。预测的基本过程为:利用经验模态分解将原始时间序列分解为更加平稳的子序列,然后利用ARMA模型对每个子序列进行建模预测,得到各个模态分量的预测值,最后再将所有预测值加在一起,最终得到对上证指数的预测结果,其步骤如下。
(1)首先利用EMD方法将前900个原始数据分解成几个不同特征尺度的IMF分量和余项。
(2)利用ARMA模型分别对前900个数据的IMF分量和余项进行建模。
(3)利用ARMA 模型对每个IMF分量和余项进行预测,再将所有预测结果相加,获得对前900个股票数据的901~1000的股票数据的预测值。
(4)最后将获得的901~1000的股票预测数据与原始数据901~1000的股票数据进行对比,评估预测误差。
2.2 EMD分解结果
首先绘制原始收盘价上证指数曲线如图1(a)所示,对收盘价上证指数的EMD分解效果如图1(b)所示。
2.3 股票的预测结果
为了验证本文所研究方法的有效性,分别对选取的股票数据利用ARMA模型和EMD-ARMA模型进行建模预测,并将其预测结果与实际股票数据进行对比,两种预测模型的预测结果,如图2中(a、b)所示。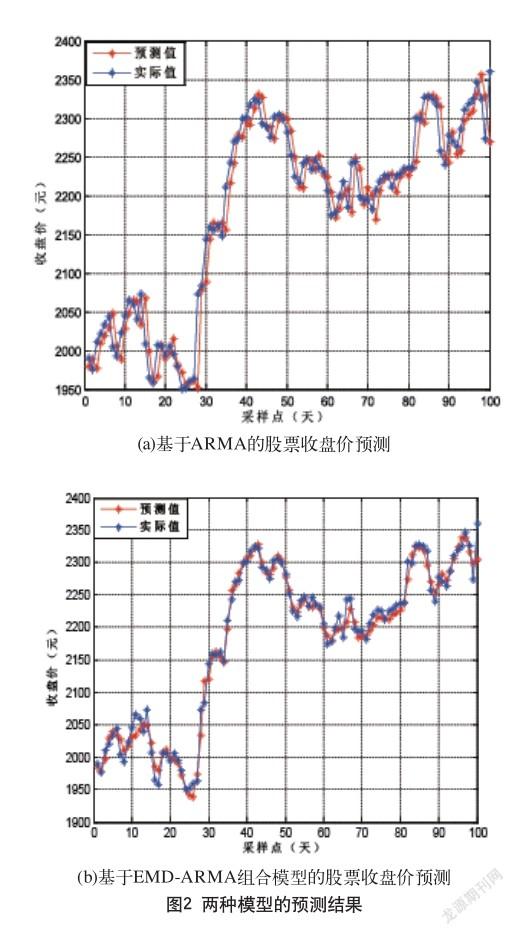
从图2中可以看出,采用EMD-ARMA模型的预测效果要优于采用ARMA模型的预测效果,预测精度得到了显著的提高,因为EMD能够将原始股票数据分解为更加平稳的子序列,能更好地找出股票数据的内在规律,使得利用ARMA模型预测使能更好地跟踪实际的股票预测数据。
表1列出了两种预测模型的误差指标大小,本文采用平均绝对百分比误差(MAPE)、 平均绝对误差(MAE)和均方根误差(RMSE)来衡量预测误差,则预测误差越小说明预测精度约好。从中可以看出,采用EMD-ARMA组合方法的误差指标要明显小于单独采用ARMA模型的预测误差指标,这同样说明了EMD-ARMA模型能明显提高股票的预测精度。

3 结语
本文研究了采用EMD-ARMA 组合的股票预测模型,得到以下结论:(1)EMD算法能将股票序列中不同特征尺度分解出来,使得分解后的数据更加平稳,规律性更强。(2)由于EMD对股票数据进行平稳化处理,极大地便利了利用ARMA模型对股票数据的建模预测过程,因此采用EMD-ARMA模型比ARMA模型的预测效果更好。
参考文献
[1] 张晨希,张燕平,张迎春,等.基于支持向量机的股票预测[J].计算机技术与发展,2006,16(6).
[2] 王玲.最优组合模型在证券市场预测中的应用研究[J].计算机仿真,2012,29(1).
[3] 李强.基于支持向量机的股票预测研究[D].山东科技大学, 2013.
[4] 谢国强.基于支持向量回归机的股票价格预测[J].计算机仿真, 2012(4).
[5] 陈恩石.基于卡尔曼滤波及神经网络算法对股价进行预测[M].
[6] 王爱平,陶嗣干,王占凤.BP神经网络在股票预测中的应用[J].微型机与应用,2010,29(6).
[7] 郑睿颖,伍应环.神经网络在股票价格预测中的研究[J].计算机仿真,2011,28(10).
[8] 孟坤,李丽.基于ARMA模型预测股票价格的实证分析[J].河北北方学院学报(自然科学版),2016,32(5).
[9] 李慧浩,許宝杰,左云波,等.基于小波变换和EMD方法提取趋势项对比研究[J].仪器仪表与分析监测,2013(3).
[10] Chen H F,Zhao W X.New Method of Order Estimation for ARMA/ARMAX Processes [J].2010,48(6).
①基金项目:国家自然科学基金项目(61671338);国家级、省级大学生创新创业训练计划项目(20160488048)。
作者简介:吴振宇(1982-),男,汉族,河南洛阳人,硕士研究生,主要从事股票预测分析方面的研究。

