基于组合赋权一理想点法的梯级水库蓄水研究

归力佳 顾圣平 林乐曼 咸京 李江林

摘要：为了协调多沙河流上梯级水库运行过程中防洪与兴利之间的矛盾，首先分析汛末提前蓄水对梯级水库防洪、兴利以及泥沙淤积的影响，然后构建梯级汛末蓄水方案多目标决策模型，利用基于粒子群的多目标搜索算法筛选出非劣解方案集，最后利用组合赋权一理想点法对非劣解集进行综合评价，得出协同优化各目标的最佳蓄水方案。将该模型应用于某流域两个串联水库的汛末蓄水研究，结果表明：根据该模型确定的蓄水最优方案与原方案相比，梯级汛末蓄满率增大了59%，多年平均年发电量增加了0.28亿kW·h，而防洪风险率与库容淤损率仅有小幅度增大。在对水库防洪安全及淤积库容影响不大的情况下，该方案较显著地提高了梯级的兴利效果。

关键词：梯级水库；蓄水方案；组合赋权；理想点法；多目标决策

中图分类号：TV697 文献标志码：A doi：10.3969/ j.issn.1000-1379.2018.05.010

随着水电能源的不断开发，大批梯级水库陆续投人运行。保障防洪安全与发挥兴利效益是梯级水库运行管理過程中的两类重要目标，而确定合理的汛末蓄水方案是平衡两类目标的有效途径。因此，梯级水库汛末蓄水时间的优化具有极为重要的现实意义。

我国不少水库群都建于多沙河流上，仅研究汛末蓄水对梯级防洪、兴利的影响是不够的，还需考虑其对泥沙淤积造成的影响。目前，已有不少学者对梯级蓄水问题进行了深入研究，如：王冬等[1]利用分析比较法，综合考虑发电、航运效益，得出梯级水库最优蓄水时间；李英海等[2]以蓄水、发电和下游补水为目标构建了梯级联合多目标蓄水调度模型；周研来等[3]利用投影寻踪法，对梯级水库蓄水时机和蓄水进程进行多目标决策。模型评价多采用传统方法，存在主观性较强或过多依赖数据和理论方法的问题。

组合赋权一理想点法作为一种多影响因子的综合评估方法，既能充分考虑专家经验，又能尽量真实反映数据的客观信息，使评价结果更加可靠，目前已成功运用在多个领域，如李影等[4]将其引入大坝安全评价中。本研究以防洪安全、蓄水、发电和减少泥沙淤积为基本目标，建立梯级水库汛末蓄水方案多目标决策模型，并将组合赋权一理想点法应用到模型的决策评价中，然后通过工程实例加以验证。

1 梯级水库汛末蓄水方案多目标决策模型

1.1 多目标决策指标的选择

1.1.1 防洪风险

汛末提前蓄水的风险是指水库在提前蓄水这段时间内，因各时刻的库水位均高于不提前蓄水时的相应库水位，有可能调蓄不了汛末所来的洪水，从而给水库防洪带来不利后果。本研究将梯级水库防洪风险率[5]作为汛末提前蓄水的风险评价指标。由于汛末不同时段洪水量级存在差异性，因此将汛末分为若干时段，分别计算水库在各时段内某一特定频率下的设计洪水过程，并通过调洪演算得出各时段内坝前水位所允许的最高值（即坝前限制水位）。

根据不同汛末蓄水方案、长序列径流资料进行蓄水模拟，得到各方案下的逐日水库水位，汛末水库坝前水位超过其对应时段内的坝前限制水位的天数记为Tθ，汛末总天数为Tm，则单个水库的防洪风险率为Rθ=Tθ/Tm。根据各水库特征库容的大小计算各水库的权重βθ，对各水库防洪风险率进行加权求和，即可得到梯级防洪风险率R，具体公式为式中：Vθ为库θ的调洪库容（对于防洪风险率的计算），或库θ的兴利（调节）库容（对于汛末蓄满率、库容淤损率的计算）；t为梯级水库级数。

1.1.2 兴利效益

梯级水库的兴利效益一般通过发电和蓄水来体现，因此将梯级水库多年平均年发电量和汛末蓄满率作为效益评价指标。通过对各方案进行长序列模拟，梯级水库多年平均年发电量E为各水库的多年平均年发电量Eθ之和：

水库汛末蓄满率Fθ为库θ汛末蓄满年数nθ与总年数N的比值，即Fθ=nθ/N。梯级汛末蓄满率F为各库汛末蓄满率Fθ与该库权重βθ相乘后相加得到的总和：

1.1.3 防淤效益

由于蓄水日期的改变会影响多沙河流的泥沙淤积状况，因此将梯级库容淤损率也作为评价指标纳人指标体系中。采用20a作为水库的淤积年限，对各方案进行长序列模拟，得到各库对应的兴利库容中的泥沙淤积量VθS，则各库的库容淤损率Sθ=VθS/Vθ。各库的淤损率Sθ与该库权重βθ的乘积之和作为有效的梯级库容淤损率S：

1.2 多目标决策模型

1.2.1 目标函数

本研究目的主要是寻求梯级水库防洪、发电、蓄水和减少泥沙淤积各目标与汛末蓄水方案之间的关系，选出满足多目标优化的梯级水库最佳汛末蓄水方案。为此，选取梯级防洪风险率R最小、蓄满率F最大、多年平均年发电量E最大和库容淤损率S最小作为蓄水优化研究的4个目标，其表达式分别为式中：x为决策变量，即梯级水库汛末蓄水方案，x=（D1、D2，…，Dθ，…，Dt），即梯级各水库开始蓄水日期的组合向量，其中Dθ为库θ汛末蓄水的开始日期。

1.2.2 约束条件

在模型计算中需要满足的约束条件有水量平衡约束、库容约束、上下游水库间水力和沙量联系、泄流能力约束、水库蓄水量约束、水电站出力约束。

除以上约束条件外，还应当补充拟定方案的取值范围，即决策变量x的取值范围：

Dθ∈[Dθmin，Dθmax] （10）式中：Dθmin和Dθmax分别为库θ汛末可以开始蓄水的最早和最晚日期。

2 多目标决策方法

2.1 方案初选

在上述约束条件下，为梯级各水库拟定若干种汛末开始蓄水日期，从而组合出梯级水库汛末蓄水初始方案。通过计算，比较分析各方案对4个目标值的影响，并据此调整初拟方案各库汛末开始蓄水日期的约束，提出新的蓄水方案集。

由于在求解实际问题过程中，过多的方案是无法直接应用的，因此采用基于粒子群的多目标搜索算法（CMOPSO）[6]从已有方案集中筛选出部分非劣解，构成一个非劣解的子集，即实现对方案的初步优选。

2.2 基于组合赋权一理想点法的梯级水库汛末蓄水方

案多目标决策

从已有方案集中筛选得到的是若干个非劣解方案，为了对这些方案的好坏进行评价决策，需要结合理想点法进行优劣排序，以选出最优汛末蓄水方案。

2.2.1 指标权重

采用理想点法对多目标方案进行评价，首先要计算出梯级防洪风险率、汛末蓄满率、多年平均年发电量和库容淤损率4个指标的权重。本研究运用嫡权法计算客观权重，并结合层次分析法计算的主观经验权重对客观权重进行调整，得出组合权重。

将计算的权重结果进行组合赋权[7]，步骤如下。

（1）对于一个基本的权重向量集U={u1，u2，…，up}，这P个向量任意线性组合成一个可能的权重集：

（2）寻找最满意的权重向量就是对线性组合权重系数ωk进行优化，优化的目标是使u*与各个uk的离差极小化，即

根据矩阵的微分性质，可知式（12）最优化的一阶导数条件为

（3）根据式（13）求出（ω1，ω2，…，ωp）后，对其进行归一化处理：

最后得出的组合权重为

2.2.2 理想点法

理想点法[8]是根据已建立的梯級水库汛末蓄水方案多目标决策指标体系，结合所求出的各评价指标的组合权重，构造规范化加权决策矩阵，并确定该决策矩阵的理想点和负理想点；然后在各非劣方案集中找到一个解，使其距离理想点最近，距离负理想点最远。该方法的具体步骤如下。

（1）将梯级水库汛末蓄水多目标决策归一化后的指标值与相应的指标组合权重相乘，得到加权决策指标：式中：ui*（i=1，2，…，m）为第i个指标的组合权重值；rij（i=1，2，…，m；j=1，2，…，n）为第j个方案第i个指标归一化后的指标值。

（2）确定理想解和负理想解：

z*=（z1*，z2*，…，zi*，…，zm*）

z*=（z1*，z2*，…，zi*，…，zm*）式中：zi*为各方案中加权决策指标i的最大值；zi*为各方案中指标i的最小值。

（3）计算每个方案的决策指标向量到理想点的距离和到负理想点的距离：

（4）计算每个方案对于理想点的相对贴近度Cj*：

按相对贴近度Cj*的大小给方案排序，Cj*越大，方案越接近理想点。

3 工程应用

A库和B库两座大（2）型水库分别是某流域梯级水库的上、下级水库，其特征参数见表1。

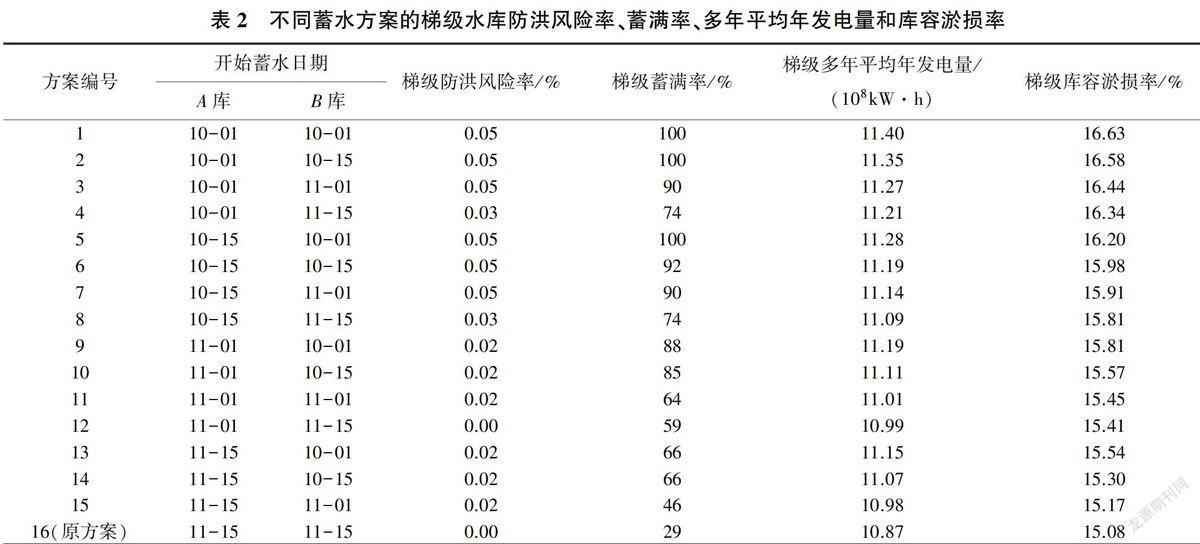
由于A、B两库汛期分期一致，后汛期均为10月1日—11月30日，因此两库汛末最早可以提前至10月1日蓄水。本研究初选了包括原设计方案在内的16个梯级水库汛末蓄水方案，见表2。

将汛末以半月为一个时段分为4段，对A，B两库各时段P=0.05%的洪水进行调洪演算，得到各库各时段的坝前限制水位，见表3。

根据表3中的坝前限制水位，针对不同汛末蓄水方案求出梯级水库防洪风险率；根据梯级水库运行调度规则，计算梯级汛末蓄满率和多年平均年发电量，并利用非均匀流不饱和全沙水库数学模型[9]计算梯级库容淤损率，结果见表2。

由表2可知：①B库开始蓄水日期一定时，A库开始蓄水日期越晚，梯级防洪风险率、蓄满率、多年平均年发电量和库容淤损率均越小；②A库开始蓄水日期一定时，B库开始蓄水日期越晚，4个指标值也越小；③若A库从11月15日开始蓄水，则梯级蓄满率不足75%；B库亦然。由于汛末蓄水不足会导致梯级水库非汛期兴利效益的损失，因此建议A、B库汛末蓄水开始日期均提前至11月1日之前。

综上所述，对于初选的蓄水方案进行优化调整：A库开始蓄水日期调整为10月1日、10月15日和11月1日；B库开始蓄水日期设为从10月1日至11月1日的所有日期。对重新拟定的方案采用基于粒子群的多目标搜索算法求得非劣解集，非劣解方案的开始蓄水日期及4个指标值的计算结果见表4。

运用层次分析法计算得到梯级防洪风险率、蓄满率、多年平均年发电量和库容淤损率4个评价指标的权重分别为0.25、0.40、0.25和0.10。根据嫡权法，计算得到4个指标的权重分别为0.46、0.11、0.16和0.27。再根据式（12）至式（15），得到4个评价指标的组合权重分别为0.36、0.24、0.20和0.20。

最后根据式（16）至式（20）计算出各方案与理想点之间的贴近度以及方案的优劣排序，见表60

由表6可知，方案13的贴近度值最大，是综合考虑防洪、兴利以及减少泥沙淤积各目标梯级水库汛末蓄水方案中的最优解。该方案中A库11月1日开始蓄水、B库10月5日开始蓄水，梯级水库防洪风险率为0.02%，汛末蓄满率为88%，多年平均年发电量为11.15亿kW·h，库容淤损率为15.72%。与原方案相比，梯级水库的汛末蓄满率增加了59个百分点，多年平均年发电量增加了0.28亿kW·h，而防洪风险率与库容淤损率分别增加了0.02个百分点和0.64个百分点。

4 结论

在梯级水库运行过程中，确定合理的汛末蓄水方案可以在一定程度上协调防洪、兴利、减淤等多个目标，从而实现综合效益的优化。以控制防洪风险、提高兴利效益和减少泥沙淤积为目标，建立了梯级水库汛末蓄水方案多目标决策模型，通过基于粒子群的多目标搜索算法筛选出非劣解集，并采用组合赋权一理想点法对非劣解进行评价决策。实例研究表明，在防洪安全得到保证的前提下，最优方案没有引起泥沙淤积的大量增加，并且发电和蓄水效益较原方案有了明显的提高，说明该模型的优化效果明显。

参考文献：

[1]王冬，李义天，邓金运，等.长江上游梯级水库蓄水优化初步研究[J].泥沙研究，2014（2）：62-67.

[2]李英海，董晓华，郭家力.三峡梯级水电站汛末联合多目标蓄水调度研究[J].水电能源科学，2015，33（9）：61-64.

[3]周研来，郭生练，陈进.溪洛渡—向家坝—三峡梯级水库联合蓄水方案与多目标决策研究[J].水利学报，2015，46（10）：1135-1144.

[4]李影，刘治愚.基于组合赋权-理想点法的大坝安全评价模型[J].中国水利水电科学研究院学报，2016，14（1）：60-66.

[5]彭杨，李义天，张红武.三峡水库汛末不同时间蓄水对防洪的影响[J].安全与环境学报，2003，3（4）：22-26.

[6]贾庭芳.基于粒子群优化的离散多目标优化算法[D].太原：太原科技大学，2011：27-37.

[7]山成菊，董增川，樊孔明，等.组合赋权法在河流健康评价权重计算中的应用[J].河海大学学报（自然科学版），2012，40（6）：622-628.

[8]方国华，黄显峰.多目标决策理论、方法及其应用[M].北京：科学出版社，2011：100-106.

[9]刘东升.水库泥沙一维数学模型研究与应用[D].大连：大连理工大学，2012：8-35.