基于灰色关联度的黄河年径流周期及预测研究

袁合才 宋倩倩 邓自源 付雪

摘要：根据黄河利津水文站161 a的年径流相关数据，采用灰色系统中的灰色关联度方法，建立了黄河年径流周期模型并进行短期预测。结果表明：利用灰色关联度方法来研究黄河年径流周期是合理可行的；黄河年径流时间序列具有5a的短周期、10a的中周期和34a的长周期，长中短周期共同主导着年径流变化；利用周期模型进行年径流短周期预测结果具有一定的可信度；2016-2020年，黄河年径流变化趋势为逐年下降，明显低于多年均值。

关键词：灰色关联度；周期模型；年径流；黄河

中图分类号：P333.1； TV882.1 文献标志码：A doi：10.3969/j.issn.1000-1379.2018.05.004

河川中长期年径流预测对于水资源的开发利用、科学管理、优化调度及防灾减灾都具有十分重要的意义。由于年径流受多因素影响而呈现出典型的非线性特征[1]，因此精确地描述其未来变化趋势是十分困难的。近年来，国内外诸多学者对年径流预测进行了较为深入的研究，但是基于年径流数据推算变化周期并利用变化周期预测未来变化趋势的方法和模型并不多见，在周期分析方面常用的方法有傅里叶分析法、谱分析法、最大嫡法及小波分析法等[2]。

基于径流形成过程的复杂性及相关影响因子的不确定性，可将径流看作含有灰因子和灰元素的灰色系统[3-4]。为了建立年径流变化周期数学模型及对未来发展趋势做出预测，本文基于黄河利津水文站1855-2015年共161a的天然年径流数据[5]，采用灰色关联度建立年径流周期模型，并利用该周期模型预测未来年径流发展趋势，以期揭示黄河年径流的变化特性，并为相关部门的优化调度提供较为准确的决策依据。

1 方法描述

1.1 灰色关联度

灰色系统理论是我国华中科技大学邓聚龙教授于20世纪80年代初提出的一种新型数学理论，灰色关联度是灰色系统中的重要组成部分，而关联度则是事物之间、因素之间关联性的“量度”。自20世纪80年代以来，邓氏关联度作为灰色系统理论的重要内容不断得以改进，根据数据时间序列本身的相关特性，不断提出了诸如绝对关联度、斜率关联度等灰色方法[6]，但其基本原理及模型框架皆为邓氏关联度。因此，本文利用邓氏关联度方法，并不过于关注影响年径流量大小的相关因素，而是从数据时间序列本身入手，结合灰色关联度的计算方法，通过分析年径流时间序列之间灰色关联度的变化，分析黄河年径流的周期变化规律。邓氏关联度[6]的计算步骤如下。

（1）确定原始序列X0、参考序列X1和比较序列Xi（i=1，2，…，m）。表达式分别为

X0=（x0（1），x0（2），…，x0（n））

X1=（x0（1），x0（2），…，x0（l））

X2=（x0（2），x0（3），…，x0（l+1））（1）

.

.

.

Xm=（x0（m），x0（m+1），…，x0（m+l））式中：n为已知径流量的年数，本文为161； m为确定的比较序列的个数；l为确定比较序列个数之后比较序列中的元素个数，由于m值的选取不一，因此l的值也是不固定的。

（2）对序列进行无量纲化。公式为

Xj'=Xj/x0（j）=（x0'（1），x0'（2），…，x0'（l））（2）式中：Xj'.为无量纲化后的序列；x0 （j）为Xj序列中的第一个元素值；x0'（l）为比较序列中的最后一个元素；j=1，2，…，m。

（3）计算差序列Δi并找出差序列的最大值M及最小值m'。公式为

Δi（k）=|Xi'（k）-X'1（k）|

Δi=（Δi（1），Δi（2），…，Δi（l））式中：|Xi'（k）-X1'（k）|为第k点Xi'与X1'差的绝对值；k为序列中的第k个元素，k=1，2，…，l。

（4）求关联系数γli（k）。公式为式中：ξ为系数。

（5）求灰色关联度γli。公式为

1.2 年径流周期

从理论上分析，黄河年径流周期并不是数学意义上严格的函数周期，而是一种趋势意义下的周期。通过求解各年径流时间序列之间的灰色关联度，可利用MATLAB软件画出灰色关联度折线图，在局部范围内，灰色关联度折线的底部称为波谷，顶部称为波峰，周期长度可以按前一波谷到下一波谷测量，也可以从前一波峰到下一波峰测量。根据黄继平等[7]的研究，利用相邻波谷之间的长度来测定周期，其结果更加稳定可靠。

2 结果与分析

2.1 模型建立

通过分析1855-2015年利津水文站的年径流数据，采用错位构造年径流序列，设原始年径流序列为X0（其中n=161），参考序列为X1，比较序列为Xi。

为了使结果更加符合年径流的实际变化情况，经分析确定构造的序列个数m为140，计算各比较序列与参考序列之间的灰色关联度并绘制折线图.见图1。

在图1中选取折线的局部最低点（见表1），计算折线局部最低点所对应的横坐标之差，即局部最低点的时间间隔△t（结果见表1）。对于长周期特征，由第1组数据可知，在所列时间间隔的7个数据中，数据17出现4次，而数据18、20、21则各出现1次，由概率统计中的众数方法，可认为年径流长周期为T=2Δt=2×17=34a；對于中周期特征，由第2组～第4组数据可知，在所列时间间隔的23个数据中，数据4出现6次，数据5出现5次，数据6出现3次，而数据7出现4次，数据分布较为均衡，因此采用概率统计中的平均数方法，由23个数据得平均时间间隔为5.51a，且由于数据4、5出现次数较多，因此可认为年径流中周期为T=2Δt=2×5=10a；对于短周期特征，由于其时间跨度较小，因此在图1中灰色关联度数据在短时间内波动幅度并不明显。根据数学模型所得的140组灰色关联度实际数据，选取后50组连续数据，绘出时间间隔分别为3、4、5、6a的4组灰色关联度的波动图（见图2）。从图2中可以看出，时间间隔为5a的灰色关联度数据波动幅度最小，从而可确定年径流短周期为T=5a。

2.2 模型检验

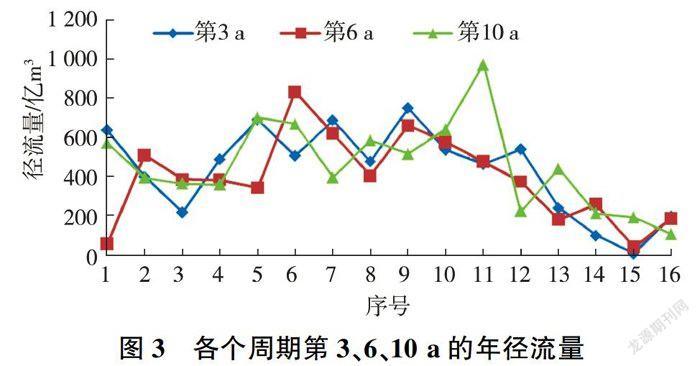
以中周期（10a）为例对黄河年径流周期灰色关联度模型进行检验。为了让可信度更高，取中周期每一周期中分布较为均匀的第3、6、10a的数据（见表2）进行分析来验证周期的可信度。由年径流数据的分布（见图3）可以看出，不同周期中同一位置的年径流前面的部分较大，后面的部分较小。因此分1～12、13～16两部分来验证中周期的可信度。从各周期第6a的数据可以看出，由于第1个和第15个数据中显示年径流数据产生了突变，影响了模型检验，因此分别取其前后两年径流量的平均值进行替换，再进行检验。经过数据处理及参考图3，可认为前半部分年径流都集中在500亿m3左右，而后半部分则都集中在220亿m3左右。同理，利用上述方法分析各周期的第10a数据，并将处于极度丰水期的第11个数据替换为前后两年径流量的均值，分析数据可以得出，前半部分和后半部分分别在一定的范围内波动。根据上述分析并经趋势线作图估计，结果表明模型计算结果具有较高的可信度。

长周期及短周期的验证类比中周期验证过程进行。结果表明，黄河利津水文站年径流短周期为5a、中周期为10a、长周期为34a是可信的。

2.3 年徑流周期特征

为了准确描述年径流周期变化特征，笔者认为年径流受3种周期的共同作用。其长中短周期的具体特征如下。

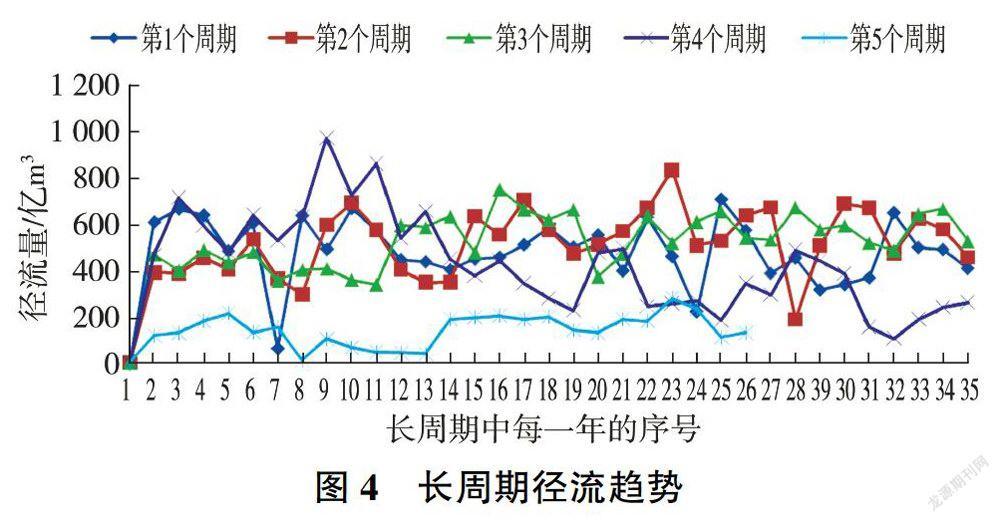
（1）长周期特征。各周期对应位置上前4个周期波动较频繁（见图4），经分析得知前3个周期的大体趋势为先下降后上升，第3个和第4个周期状态不稳定，处于过渡阶段；第5个周期大体上为下降周期。

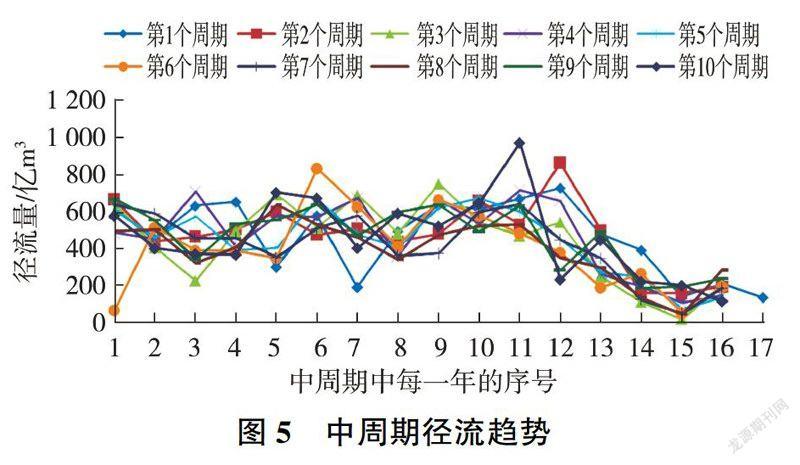
（2）中周期特征。各周期的对应位置上，前3个周期整体上为下降周期，且在第3个周期达到最低点；接着径流量开始增大，在第6个周期达到峰值（见图5）。如此循环，在第8个周期降至最低点，且在后续第11个周期达到峰值。随后几个周期对应位置上的径流量整体处于较为明显的大幅下降趋势中，且在第15、第16个周期达到谷底，而第16个周期则存在稍微的上升趋势。

（3）短周期特征。各周期对应年份的年径流量均在一定范围内波动，且波动幅度相似。前4个周期整体为下降周期，且在第2个周期达到波谷。然后，年径流量变化总体呈小幅缓慢上升态势，一直到第28个周期年径流达到峰值，之后便整体呈下降趋势。

2.4 模型预测

以2013年黄河年径流量为例介绍模型的趋势分析及其预测应用。

根据长中周期组合可知，2013年处于第5个长周期的第23a和第16个中周期的第9a，其趋势处于长周期的下降阶段和中周期的上升阶段，故根据其趋势可预测2013年的年径流量应小于2003年的年径流量，且大于1979年的年径流量，即年径流量为192.60亿～270.08亿m3。因中周期对应年份2003年与2013年比较相近，故中周期对其影响较大，2013年的年径流量应大于年径流区间的中值。结合2013年实际年径流（236.9亿m3）可知预测结果比较符合实际情况。

根据上述的趋势分析过程可以进行短期预测。由模型运算结果可知2016年处于第5个长周期的第26a和第17个中周期的第2a。其趋势处于长周期和中周期的下降阶段，分析得知2016年的年径流应低于240亿m，。2016-2020年这5a均处在长中周期的下降阶段，径流量受短周期影响虽有小幅度上升，但总体趋势仍是下降的。因此，受长中短三种周期的共同作用，可以得出2016-2020年黄河年径流量整体呈下降趋势。

3 结论

采用灰色关联度法建立了黄河年径流周期模型，并利用周期模型所得结果预测了2016-2020年的年径流变化趋势。计算表明，在黄河年径流的科学研究中，引入灰色关联度来探讨其周期演变规律是合适的，理论分析结果较为符合实际，具有较高的可信度和较大的实践价值。但是，灰色关联度理论体系也是不断发展的，如何通过考察黄河年径流时间序列的具体特征，构造更加符合其演变特征的具体的灰色关联度模型，是进一步研究的方向。

参考文献：

[1]张少文，何伟，王文圣，等.黄河天然年径流超长期变化特性研究[J].人民黄河，2004，26（8）：10-12.

[2]赵利红.水文时间序列周期分析方法研究[D].南京：河海大学，2007：1-64.

[3]饶素秋，霍世青.灰色系统模型在黄河径流分析预测中的应用[J].人民黄河，1997，19（7）：39-42.

[4]李正最.以灰色关联度分析为基础的河川径流预测方法[J].浙江水利科技，1992（4）：10-15.

[5]黄河水利委员会.黄河水资源公报[R].郑州：黄河水利委员会.[2017-05-15].http：//www.yellowriver.gov.cn/other/hhgb/.

[6]刘思峰，蔡华，杨英杰，等.灰色关联分析模型研究进展[J].系统工程理论与实践，2013，33（8）：2041-2046.

[7]黄继平，黄良文.中国股市波动的周期性研究[J].统计研究，2003（11）：9-14.