电池交换式电动汽车换电站选址优化方法

顾腾飞 张勇

摘 要：為实现电动汽车快速补能，面向电池交换的充电方式，研究了城市路网上电动汽车换电站的选址问题。首先研究了电动汽车用户的路径选择，基于交通网络均衡状态和换电站选址方案的相互影响，建立站点建设成本和出行成本之和最小为目标的换电站选址优化模型。然后预测不同方案下的交通网络均衡状态，并依据预测结果评价选址方案的优劣，最后设计求解算法，利用襄阳东津新区的路网及居民出行数据进行算例分析，验证模型及算法的可靠性，求得换电站的最优选址及换电需求。研究表明，建立的电池交换式电动汽车换电站优化模型可以获得路网路段流量及换电站处的换电需求量，给出最优的选址方案及换电站建设时序;电动汽车混入率对换电站布设、交通网络均衡状态有较复杂的影响;交换站数量的增加能减少出行成本，但边际作用递减。研究结果可为城市换电站的规划提供决策参考。

关键词：最优化;交通规划;换电站规划;用户均衡模型;电动汽车;电池交换

中图分类号：U491.25    文献标志码：A

Optimization method of locations of recharging stations

for electric vehicles with battery swapping

GU Tengfei1， ZHANG Yong2

（1.General Planning Research Division， JSTI Group，Nanjing， Jiangsu  210000， China;2. School of Railway Transportation， Soochow University， Suzhou， Jiangsu 215131， China）

Abstract：In order to realize rapid recharge for electric vehicles（EV）， the locations of recharging stations for electric vehicles on city road network are studied with battery swapping charging mode. To this end， the path choice of electric vehicles is studied and an optimal location model of battery-swapping stations is proposed based on the relationship between the network user equilibrium and the deployment of battery-swapping stations， with the objective of minimizing the sum of station construction cost and travel cost; The network user equilibrium under different schemes is predicted and the corresponding scheme is evaluated due to the predicted results. And then the solution algorithm is designed.

A computational study was performed based on transportation network and resident trip data of Dongjin New District in Xiangyang， Which confirms the reliability and practicability of the model and algorithm proposed.

Then the optimal deployment of the recharging stations and the battery-swapping demands are obtained.

The research shows that the optimization model of battery-swapping station can achieve the link flow of road network， the demand of battery swapping at stations， optimal deployment and construction sequences of the stations. The penetration of EVs has a more complicated impact on the deployment of swapping stations and the traffic network equilibrium. The increase of swapping station's number can reduce the travel cost， but the marginal effect is diminishing. The research results can provide decision-making basis for the planning of urban swapping stations.

Keywords：

optimization; transportation planning; swapping station planning; user equilibrium model; electric vehicle; battery swapping

电动汽车具有高能效、低污染的优点，发展前景较好。不过因受续航里程和充电设施的制约，目前其应用仍未得到大规模普及。为解决传统充电方式充电时间长的弊端，电池交换模式应运而生。对于有充电需求的电动汽车，将其耗尽的电池取下，即刻换上满电电池便能使其继续行驶，这种方式能有效减少出行者途中延误的情况发生。因此换电站点的布设问题亟待解决。

目前，换电站布设方法已经有了初步的探索。MAK等[1]建立了成本最低和目标导向2个选址模型，后者能更快给出优化方案。NIE等[2]以社会总成本最小为目标建立模型，研究电池容量和充电功率的选择，发现换电模式的竞争优势在电动汽车高混入率、高服务水平下更为明显。由于研究对象为单一线路，因而对路径选择问题未深入探究。而在这一方面部分学者进行了相关研究，ADLER等[3]提出电动汽车路径导航模型，导航结果可降低出行者平均等待时间，并能够根据导航结果给出电池储备计划;YANG等[4]面对换电站布设和路径选择问题，采用整数规划模型进行研究，并对经济和环境影响进行系统分析。但上述研究并未深入分析交通网络状态;另外，JAMIAN等[5]还利用人工蜂群算法优化换电站布局及规模，给出的方案能有效减少配电网电能损失，并提高换电系统稳定性。钱斌等[6]、ZOU等[7]、WU等[8]还研究了电动公交的换电站布设、换电位和电池保有等问题。WANG等[9]针对电动出租车的换电需求也进行了相关探索。此外，还有一些学者进行了站点内部的电池充、换电安排以及根据一日内用电价格波动提出降低成本的充电措施等研究[10-12]。上述研究忽略了交通网络是一个整体，换电站及电动汽车是交通网络的一部分，脱离交通网络状态而仅考虑换电站布设问题，给出的优化方案有一定的局限性。

此外受到换电站的限制，有换电需求的电动汽车需要选择带有换电站点的路径，其路径选择与普通燃油汽车有很大的差别，因而在电动汽车混入状态下，传统的网络均衡状态会受到影响。为此，一些学者进行了相关探索。JING等[13-15]提出了3个电动汽车、燃油汽车混行状态下的交通网络均衡状态模型，但这些模型仅讨论了距离约束，没有考虑充电站点的限制。而HE等[16]研究的交通网络模型对此进行了拓展，考虑了传统充电站点的限制。杨扬等[17]还研究了电动汽车混入状态下的随机用户均衡分配模型，该模型针对的也是传统整车充电模式的电动汽车。XU等[18]对此进一步拓展，建立了基于换电站点的交通网络模型，并通过改善Laporte 和Pascoal的最短路算法[19]，提出了解决电池交换式电动汽车出行最短路径的多标签算法。这些研究侧重于网络均衡状态，是在充、换电站点及其配置给定的情况下，对交通网络均衡状态的研究，忽略了充电设施的规划。

综上所述，以往研究往往将交通网络均衡状态和换电站选址规划孤立开来，这与现实情况有较大差距。事实上，充电设施的配置影响着用户的路径选择，而用户的充电需求也影响着充电设施的配置。基于此，笔者首先研究了有换电需求的电动汽车前往目的地的路径选择，考虑网络均衡状态和换电站选址的相互影响，以站点建设成本和出行成本之和最小为目标，建立了换电站选址优化模型。依据所建模型，研究了不同充电设施配置情况下的用户均衡状态，并据此评价相应选址方案的优劣，最后确定最优的选址方案，得到各站点换电需求;并以所建模型为工具，展现其在优化换电站选址上的应用。

1 模型构建

1.1 路网元素及基本假设

笔者仅考虑城区范围的通勤客流，忽略非通勤客流的影响。假设研究范围内的路网G由路段和节点组成，记为G=（N，A），其中，N为节点集合，A为路段集合。R N、S N分别表示研究范围内所有出行的起讫点集合。路网上的路段a表示为a=（i，j）∈A，其中i，j∈N。路段a的自由流出行时间为t0a，路段a上的流量记为xa。为方便建模，进行如下基本假设。

A1：路网上仅有电动汽车和燃油汽车，路段a上的流量xa包括有换电需求的电动汽车流量（记为xea）、燃油汽车和没有换电需求的电动汽车流量（记为xga），即xa=xea+xga。

A2：出行者总会选择阻抗最小的路径，电动汽车在路段a上的能耗僅与其实际出行时间成正比。同时假设所有电池的容量相等，进行一次电池交换的费用相等。

A3：城区内通勤客流出行距离一般较小，因此，往往经过多次出行才需进行一次电池交换，且假设需要换电的那次出行，电动汽车司机总可以在电池电量耗尽前到达换电站点进行电池交换，且假定司机在到达换电站前是无法准确预知排队等待时间的。

1.2 换电需求分析

根据假设A3，通常情况下，电动汽车的电量是完全可以满足一次出行需求的，因而一般情况下可将其视为普通汽车。在这种情况下，根据假设A2可知，出行者总会选择阻抗最小的路径，达到交通网络的均衡状态。对于同一起讫点r和s间的通勤客流来说，在均衡状态下的出行时间是相等的，且是所有可能的出行路径中最小的，用户无法通过擅自改变路径而得到更小阻抗的出行路径，令均衡状态下r和s间的出行时间为trs。记电池容量为E，电动汽车行驶单位时间的能耗为Q，根据假设A2，一块满电电池可以供电动汽车行驶的时间为E/Q。那么，对于r和s间使用电动汽车出行的用户来说，平均经过（E/Q）/trs次出行将会产生一次换电需求。换言之，单位时间内所有r和s间出行的电动汽车中，有trs/（E/Q）比例的电动汽车需要进行电池交换，这个比例称为换电需求比例，记为ηrs。即：

ηrs=trsE/Q。 （1）

值得注意的是，不同出行起讫点（下文简称OD对）间的换电需求比例是不一样的，这里仅以r和s间的出行需求为例进行说明。

在电动汽车电量将要耗尽时，司机为完成换电便会放弃原来具有最小阻抗的路径，而选择途经换电站的路径，下面分析车辆的路径选择问题。

燃油汽车及没有换电需求的电动汽车的最短路可由Floyd算法求得。Floyd算法是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法，借助距离矩阵的迭代运算来求解最短路的算法，一次可获得任意2点间的最短路。将交通网络看成加权图，节点为图中的节点，路段为图的边，路段阻抗为对应边的权重，这样便可利用Floyd算法求不同OD对间的最小路径阻抗。

而对于有换电需求的电动汽车，其起讫点间的出行分为2次出行，一是从起点到换电站点最短路出行，二是换电站点到终点的最短路出行。这2次出行的最短路径可由Floyd算法求得。而电动汽车在起讫点间出行总成本即为这2个最短路出行成本与换电费用之和。对同一起讫点间经过不同站点最短路的出行总成本比较，其中具有最小总出行成本的路径即为有换电需求的电动汽车最短路径。

此外，在所有的出行中，都有电动汽车的参与。假设对所有OD对，电动汽车混入的比例都是相同的，下文称为电动汽车的混入率，记为v。令qrs表示r和s间总出行需求量，那么qrsv便表示 r和s间所有电动汽车的出行量。此时可算得有换电需求的电动汽车出行量为qrse=（qrsv）ηrs，用qrsg表示r和s间无需换电的出行量，其包含燃油汽车和没有换电需求的电动汽车，则有：qrsg=qrs-qrse。

1.3 换电站选址优化模型

针对换电站选址问题，笔者提出了一个以站点建设成本和电动汽车用户出行成本之和最小为目标的优化模型（本段涉及的成本均以年为时间单位进行讨论）。换电站建设总成本，记为CI;用户的出行总成本，记为CT。则目标函数为

min Φ=CI+CT， （2）

令一个换电站基本建设成本为C0，换电站使用年限为T1，那么一个换电站分摊到一年上的建设成本为C0/T1。用xi表示第i个候选节点是否建站，即：

xi=[JB（{]1， 在节点i处设站， 0， 在节点i处不设站，

令候选节点数为k，那么所有换电站的年总建设成本为

（3）

电动汽车的出行成本包括路上行驶的时间成本、换电费用。根据假设A2可知电池交换费用是一致的，这里记为θ。这里忽略电池交换及在换电站等待换电的时间。那么，路网上总出行成本包括2部分：一是所有车辆在路网上的总的旅行时间;二是有换电需求的电动汽车在换电站的换电费用。因此路网上总时间成本为

CT=[JB（（]∑[DD（]a∈A[DD）]caxa+∑[DD（]ki=1[DD）]（xiyiθ）α，（4）

其中：ca为单位时间内路段a上的出行时间成本;yi表示单位时间内站点i的换电需求;α为单位时间的成本转换为以年为时间单位的成本的换算系数，根据高峰小时系数和一年的天数计算确定。ca可由路段a上的出行时间ta与用户出行的时间价值β确定。车辆在路段a上的旅行时间与路段流量相关，本文采用美国联邦公路局的BPR函数计算路段阻抗，即

ta（xa）=t0a（1+λ（xa/Ca）），a∈A， （5）

其中：t0a为路段a上的自由流旅行时间;Ca是路段a的通行能力;λ，是参数。

下面分析交通网络均衡状态，用Krsg表示r和s间燃油汽车和无需换电的电动汽车的路径集合，frsγ表示路径γ∈Krsg上无需换电的车流量，用Krse表示r和s间有换电需求的电动汽车的路径集合，frsg表示路径ε∈Krse上需要换电的车流量，δrsa，γ表示路径γ与路段a的相关变量，δrsa，ε表示路径ε与路段a的相关变量，δrsi，ε表示路径ε与节点i的相关变量，即

δrsa，γ=1， 路径γ经过路段a， 0， 路径γ不经过路段a，

δrsa，ε=1， 路径ε经过路段a， 0， 路径ε不经过路段a，

δrsi，ε=1， 路径ε经过站点i并进行换电， 0， 其他。

在交通网络均衡状态下，路网上的交通流，包括有换电需求的电动车以及无换电需求的车辆，其交通流分布应满足交通网络Beckmann模型，即

min β∑[DD（]a∈A[DD）]∫xga+xea0ta（xa）dx+θ∑[DD（]i∈I[DD）]yi， （6）

s.t. ∑[DD（X]γ∈Krsg[DD）]frsγ=qrsg，r∈R，s∈S，

xga=∑[DD（X]r∈R[DD）] ∑[DD（X]s∈S[DD）] ∑[DD（X]γ∈Krsg[DD）]frsγδrsa，γ，a∈A，

xea=∑[DD（X]r∈R[DD）] ∑[DD（X]s∈S[DD）] ∑[DD（X]ε∈Krse[DD）]frsεδrsa，ε，a∈A，

yi=∑[DD（X]r∈R[DD）] ∑[DD（X]s∈S[DD）] ∑[DD（X]ε∈Krse[DD）]frsεδrsi，ε，i∈I。

A為路段集合，I为换电站址集合。

2 求解算法

针对换电站选址优化模型，采用迭代加权法（简称MSA）不断逼近交通网络均衡状态。MSA配流方法是介于增量分配法和平衡分配法之间的一种循环分配方法，不断调整各路段分配的流量而逐渐接近平衡分配结果。每步循环中，根据各路段分配到的流量进行一次0-1分配，得到一组各路段的附加流量;用该循环中各路段的已有流量和分配的附加流量进行加权平均，得到下一循环中的分配交通量;当相邻两次循环中分配的交通量十分接近时，即停止运算，最后一次循环中得到的交通量即为最终结果。而本文中除了普通汽车流量外，还需要进行加权迭代的有电车流量及换电流量。

换电站选址是在拥有建站条件的候选站址范围内进行的，遍历所有可能的站点设置方式，得到每种方案下交通网络均衡状态，并结合设站数量计算相应的目标函数（2）的值，从而选择最优的换电站选址方案。在不考虑电动汽车换电、将其视为普通汽车的情况下，用MSA交通流分配方法得到用户均衡状态，并计算该状态下各OD对间出行的阻抗值。依据式（1）计算单位时间内有换电需求的电动汽车所占比例，进而结合电动汽车混入率可计算出单位时间换电需求。生成所有可能的换电站选址方案解集，设所有可行的换电站选址方案的数量为nmax，第n个选址方案记为sn，其目标函数（2）对应的值记为Φn，最优选址方案记为s*，其目标函数值记为Φ*。具体算法如图1所示，其中ε是预先设定的收敛精度，收敛精度也可以用迭代次数控制。

3 算例分析

3.1 算例设置

本节以襄阳市东津新区2020年的规划路网及预测OD对为基础进行算例分析。提取襄阳东津新区规划的主次干路、主要支路和城市快速路，抽象成如图2所示的路网。其中包含116个节点、205条路段，并取主要的2 768个OD对，其中1—13号节点是候选站址。

参考以往研究文献[1]和文献[20]，本例假设电动汽车的电池容量为24 kW·h，电动汽车每小时大约耗电8 kW。根据假设A3可得，一块满电电池可以连续运行约3 h。BPR函数中的参数λ=0.15，=4。单次换电费用为100元，用户路上行驶与换电站内接受服务的时间价值均为40元/h。根据特斯拉的换电站建设情况[21]，单个换电站的建设固定成本为300万元，使用寿命为60年（按建筑使用年限推算）。高峰小时换算成年为单位的换算系数a=2 920（一年按365天计算，高峰小时系数取12.5%）。

3.2 换电站选址优化分析

电动汽车混入率对建站数和选址均有较大影响，因而本节就从混入率对站点数量和选址的影响进行分析。由于电动汽车受到政策的支持，其市场占有率会随时间推移不断提高，而混入率发生变化又会对最优的选址方案产生影响。图3展示的不同电动汽车混入率对应的最优建站数量。图4展示的是不同混入率下最优的设站位置，其中黑色点表示该混入率下在该节点设站。由图3可知，最优建站数随混入率增加而增加。但混入率提高到一定程度时，最优建站数便不再增加，如本例混入率超过70%时，最优的建站数始终为8个，不再继续增加。由图4可知，模拟的各种混入率的最优选址方案集中在4，6，10，11及13这几个候选节点设站，这是因为这些节点处于各出行路径集中的区域，更可能成为最优选址方案中的设站位置。同时可以发现，当混入率较低时，节点9是最优选址方案中的设站位置，但混入率较大时，节点9反而不在最优选址方案中。节点3在低混入率时不在最优选址方案中，但混入率较高时，反而成为最优选址方案的设站位置。由此可见，可以尝试先在4节点、10节点设站，因为无论混入率如何变化，4节點、10节点均是最优选址方案中的设站节点。

综合图3—4可知，建站数并非越多越好，也不是越少越好，决定建站个数时需要立足长远，根据混入率慎重选址。另外要注意换电站的建设时序，可以优先建设不同混入率下均选择设站的节点，这些站点总是在最优选址方案中，不因混入率变化而改变，这样可以避免投资浪费。

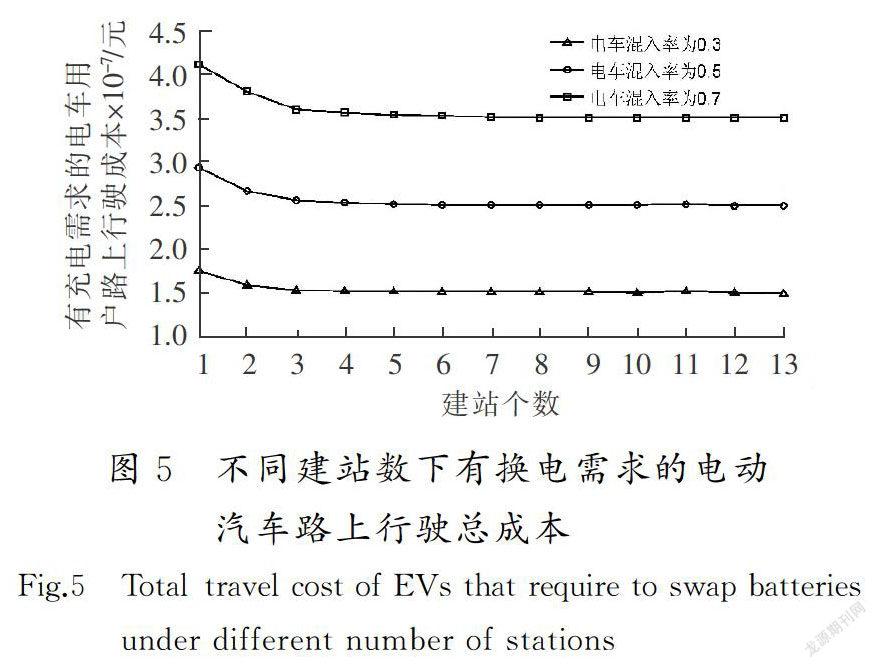
换电站数量及位置直接影响到有换电需求的电动汽车用户的出行，因而本节首先分析选址方案对有换电需求的电动汽车用户出行成本的影响。图5展示的是建站数对有换电需求的电动汽车用户出行成本的影响。可以看到，当建站数较少时，电动汽车用户的年总出行成本会随着建站数的增加而迅速降低，这是因为建站数增多，部分电动汽车用户不需迂回绕行去换电，因而减少了出行成本;但是当建站数进一步增加，尤其是超过6个的时候，总出行成本便趋于平稳，仅有缓慢的下降趋势。这说明随着站点数的增加，其降低有换电需求的电动汽车用户出行成本的作用越来越弱。换电站选址影响有换电需求的电动汽车路径选择和路段流量分布，进而影响了其他用户的路径选择，从而影响了整个路网的用户出行成本。图6展示的是建站数量对所有车辆年总出行时间的影响：当建站数较少时，路网上所有车辆的总出行时间随建站数量增加而迅速降低，且混入率越高，总出行时间的下降越明显。这是因为在高混入率下，有换电需求的电动汽车用户相应较多，那么建站数增加时，可以减少绕行的用户就更多，因而总出行时间下降更为明显;但是当建站数进一步增加，所有车辆的年总出行时间便趋于稳定，且不同混入率下的年总出行时间相差较小。由上述分析可知，有换电需求的出行者的出行成本、路网上全部车辆的出行成本都会随着建站数的增加而减少，但当建站数量增加到一定程度时，其对用户出行成本降低的作用会越来越弱。

换电站选址影响交通网络均衡状态，进而对路段交通量、电池交换需求产生较大影响。本节以混入率为50%为例，分析换电站选址对交通网络均衡状态的影响。交通网络均衡状态下，路段饱和度、交通量以及电池交换需求量如图7所示。由图7可知，东津新区中心商务区的路段交通量较大，路段饱和度较高，位于中心商务区重要节点的站点4电池交换需求量较大。此外，由于节点6、节点10也是区内通勤出行经常经过的节点，因此周边路段饱和度及交通量较大，电池交换需求亦较大。而节点11、节点13位于开发强度较低的偏远地区，因而交通流及饱和度较小，但节点11、节点13仍是最优选址方案中的节点，这是因为若这两个节点不设站，那么部分电动汽车需要绕行较远距离才能完成电能补充。虽然这部分绕行的电动汽车流量的绝对数量不大，但过远的绕行仍会增加较多的社会成本，影响电动汽车用户出行的满意度。由此可见，站点选址既要考虑在交通流量及周边路段饱和度较大的区域布设，同时也要考虑站点在整个区域范围分布的均衡性，这样才能给出社会总成本较小，整个区域公众满意度较高的选址方案。

4 结 语

1）提出的换电站选址优化模型可以分析电动汽车的路径选择，利用迭代加权法预测交通网络均衡状态，得到换电站处的换电需求，并给出最优选址方案。

2）电动汽车混入率对站点建设数量及其位置有较大影响，有换电需求的出行者的出行成本和路网上全部车辆的出行成本随换电站数量的增加而减少，但当站点数量增加到一定程度时，其出行成本降低的作用便越来越弱。

3）在完全信息化的时代，充电站、电池状态及司机对需求和供给的了解会很透明，不是完全随机的，这将影响用户出行的路径选择，并由此影响换电站选址，如何考虑这些影响还有待进一步深入研究。

4）换电站内电池数量也是换电站规划的重要因素，依托本文模型得到的换电需求，可以进一步研究电池交换站内电池数量的配置问题。

5）充换电设施布设完成后，需要合理的运营方案，因此后期运营问题也是重要的研究方向，在运营成本、盈利问题等方面可进一步深入研究。

参考文献/References：

[1] MAK H Y， RONG Y， SHEN Z J M. Infrastructure planning for electric vehicles with battery swapping[J]. Management Science， 2013， 59（7）： 1557-1575.

[2] NIE Y， GHAMAMI M. A corridor-centric approach to planning electric vehicle charging infrastructure[J]. Transportation Research Part B：Methodological， 2013， 57：1-19.

[3] ADLER J D， MIRCHANDANI P B. Online routing and battery reservations for electric vehicles with swappable batteries[J]. Transportation Research Part B：Methodological， 2014， 70：285-302.

[4] YANG Jun， SUN Hao. Battery swap station location-routing problem with capacitated electric vehicles[J]. Computers & Operations Research， 2015， 55（1）： 217-232.

[5] JAMIAN J J， MUSTAFA M W， MOKHLIS H， et al. Simulation study on optimal placement and sizing of battery switching station units using artificial bee colony algorithm[J]. International Journal Electrical Power and Energy Systems， 2014， 55（2）： 592-601.

[6] 錢斌， 石东源， 谢平平， 等. 电动公交车换电站——电池充电站优化规划[J]. 电力系统自动化， 2014， 38（2）： 64-69.

QIAN Bin， SHI Dongyuan， XIE Pingping， et al. Optimal planning of battery charging and exchange stations for electric vehicles[J]. Automation of Electric Power Systems， 2014， 38（2）： 64-69.

[7] ZOU Fuqiang， LIU Nian， LU Xinyi. Optimal configuration for battery switch stations of electric buses[C]// IEEE. 2014 IEEE Transportation Electrification Conference and Expo， Asia-Pacific （ITEC Asia-Pacific）. Piscataway： IEEE， 2014： 1-5.

[8] WU T H， PANG G K H， CHOY K L， et al. An optimization model for a battery swapping station in Hong Kong[C]//IEEE. 2015 IEEE Transportation Electrification Conference and Expo （ITEC）. Piscataway： IEEE， 2015： 1-6.

[9] WANG Yang， HUANG Liusheng， WEI Hao， et al. Planning battery swapping stations for urban electrical taxis[C]// IEEE. 2015 IEEE 35th International Conference on Distributed Computing Systems. Piscataway： IEEE， 2015： 742-743.

[10]RAVIV T. The battery switching station scheduling problem[J]. Operations Research Letters， 2012， 40（40）： 546-550.

[11]YANG Shengjie， YAO Jiangang， KANG Tong， et al. Dynamic operation model of the battery swapping station for EV （electric vehicle） in electricity market[J]. Energy， 2014， 65（1）： 544-549.

[12]SARKER M R， PANDI H， ORTEGA-VAZQUEZ M A. Optimal operation and services scheduling for an electric vehicle battery swapping station[J]. IEEE Transactions on Power Systems， 2015， 30（2）： 901-910.

[13]JIANG N， XIE C， WALLER S. Path-constrained traffic assignment[J]. Transportation Research Record： Jouranl of the Transportation Research Board ， 2012， 2283（3）： 25-33.

[14]JIANG N， XIE C. Computing and analyzing mixed equilibrium network flows with gasoline and electric vehicles[J]. Computer-Aided Civil and Infrastructure Engineering， 2014， 29（8）： 626-641.

[15]JIANG N， XIE C， DUTHIE J C. A network equilibrium analysis on destination， route and parking choices with mixed gasoline and electric vehicular flows[J]. Euro Journal on Transportation and Logistics， 2014， 3（1）： 55-92.

[16]HE Fang， WU Di， YIN Yafeng， et al. Optimal deployment of public charging stations for plug-in hybrid electric vehicles[J]. Transportation Research Part B：Methodological， 2013， 47： 87-101.

[17]楊扬，姚恩建，王梅英，等.电动汽车混入条件下的随机用户均衡分配模型[J].中国公路学报，2015，28（9）：91-97.

YANG Yang， YAO Enjian， WANG Meiying， et al. Stochastic user equilibrium assignment model for electric vehicle under hybrid traffic condition [J]. China Journal of Highway and Transport， 2015， 28（9）： 91-97.

[18]XU M， MENG Q， LIU K. Network user equilibrium problems for the mixed battery electric vehicles and gasoline vehicles subject to battery swapping stations and road grade constraints[J]. Transportation Research Part B： Methodological， 2017， 99： 138-166.

[19]LAPORTE G， PASCOAL M M B. Minimum cost path problems with relays[J]. Computers & Operations Research， 2011， 38（1）： 165-173.

[20]AVCI B， GIROTRA K， NETESSINE S. Switching-station electric vehicles： Adoption and environmental impact[J]. Institute for Operations Research and the Management Science， 2015， 61（4）： 772-794.

[21]NEIL M. Tesla Unveils Battery-swapping Tech for Fast Car Charging[EB/OL]. https：//en.wikipedia.org/wiki/Tesla_Supercharger#Tesla_station， 2013-06-21/2017-11-15.