基于模态应变能密度理论的网架结构损伤识别方法

刘卫然 杜守军 张丽梅

摘 要：为了研究网架结构的损伤检测方法，根据应变能密度理论，提出采用单元模态应变能密度差值作为网架结构损伤识别指标的方法，以损伤单元模态应变能密度差值的大小初步确定单元的损伤程度。分析了5种具有代表性的损伤工况，并在数值计算结果中引入了白噪声。结果显示，在一阶模态下，针对单损伤、多损伤和轻微损伤、严重损伤等不同损伤工况，损伤杆件的模态应变能密度差值均为高值。因此，该方法可以有效识别出网架结构的损伤位置，根据损伤单元的模态应变能密度差值大小初步确定单元的损伤程度，且在一定的噪声水平下具有较强的鲁棒性，对网架结构损伤识别具有参考价值。

关键词：结构设计;杆件结构;损伤识别;模态应变能密度;噪声鲁棒性

中图分类号：TU312   文献标志码：A

Identification of grid structure damage based on the

theory of modal strain energy density

LIU Weiran， DU Shoujun， ZHANG Limei

（School of Civil Engineering， Hebei University of Science and Technology， Shijiazhuang， Hebei 050018， China）

Abstract： In order to study the method of detecting grid structure damage， this paper proposes to use elemental modal strain energy density difference as an index of identifying grid structure damage according to the theory of strain energy density， thus preliminarily determining the degree of elemental damage. A numerical analysis is performed on five typical working conditions of damage， and white noise is introduced in numerical computation. The results show that for different working conditions of damage， including single damage， multiple damage， slight damage and severe damage， the modal strain energy density differences of the damaged member in the first-order mode remain high. Therefore， this method can effectively identify the damaged location of the grid structure and preliminarily determine the degree of element damage according to the size of the modal strain energy density difference. Furthermore， it exhibits strong robustness at a certain noise level and provides a reference for the identification of grid structure damage.

Keywords：structural design; member structure; damage identification; modal strain energy density; noise robustness

空間网格结构受力合理、刚度大、自重轻，能够满足各种建筑结构形式的要求，然而，在长期服役期间结构可能产生各种损伤，如果损伤积累到一定程度且没有及时被发现，可能会造成重大事故。例如，1978年，美国康涅狄格州哈特福市中心体育馆由于突降暴雪引起压杆失稳倒塌;2004年，巴黎戴高乐机场候机厅部分顶棚出现坍塌，造成了巨大的经济和人员生命损失。开展对网架结构的早期损伤研究，在早期阶段发现结构的损伤位置及程度，及时采取补救措施，杜绝安全隐患，具有较好的应用价值。因此，国内外学者对结构损伤识别的研究非常多。SHI等[1-2]提出了基于模态应变能的损伤检测方法，并将单元模态应变能变化率作为损伤定位指标，对平面桁架和框架结构进行了数值分析和实验研究;HA[3]详细论述了模态应变能指标的发展历程，基于模态应变能的损伤识别综合考虑了频率、振型及刚度变化等因素的影响，对损伤具有较强的敏感性。众多学者对单元模态应变能法进行了深入研究，成功应用到各种结构的损伤识别中[4-8]。李永梅等[9]采用损伤结构前后的低阶单元应变模态差作为结构损伤定位的动力指纹，建立一种基于杆单元模态应变的结构损伤定位方法，对网架结构进行了损伤诊断研究;宋玉普等[10]、王孟鸿等[11]、张丽梅等[12-14]从不同方向研究了损伤识别方法，并应用在网架损伤识别检测中，取得了一定的效果。

本文根据应变能密度理论，提出基于单元模态应变能密度差值作为网架结构损伤识别指标的方法，并应用于正放四角锥网架结构的损伤识别中。数值模拟结果表明，此方法可以利用低阶模态获得较好的损伤定位和损伤程度预测，验证了本方法的有效性。

1 模态应变能密度基本方法

应变能是指物体在外力作用下产生变形时其内部所储存的能量，单位体积的应变能称为应变能密度，不管单元体承受的是拉压应力或者是剪应力，应变能密度都可以综合反映单元体内各应力分量的作用。结构受到外界因素影响时的每一状态下，每个单元都能够存储一定的应变能，不同位置单元能够存储的应变能也不一样，结构损伤后的应变能密度变化也不尽相同，因此可通过不同单元体能量密度的变化情况来评价单元是否损伤。

根据应变能密度理论及振动理论，每个单元的模态应变能密度方程可由式（1）表示，

MSEDij代表结构损伤前第j个单元关于第i阶模态应变能密度。

MSEDij=dWijdVj=∫εij0δijdεij。（1）

同理，结构损伤后第j个单元关于第i阶模态应变能密度（MSEDdij）如式（2）所示。

MSEDdij=dWdijdVj=∫εdij0

δdijdεdij。（2）

式中：δij，εij分别表示单元体内的模态应力及模态应变，上标‘d表示结构损伤。由于损伤单元处刚度降低，产生应力集中，损伤处的应变及应力均增大，所以损伤单元的模态应变能密度远远大于未损伤单元的模态应变能密度，根据这一特性，定义结构破损前后的第j单元关于第i阶模态的单元模态应变能密度差（简称MSEDCij）作为损伤识别指标，如式（3）所示。

MSEDCij=abs（MSEDdij-MSEDij） 。 （3）

由于空间网架结构中杆件的受力主要为轴力，忽略剪应力，所以式（3）可简化成式（4）。

MSEDCij=abs（12δdijεdij-12δijεij）。 （4）

由式（4）可知，结构发生局部损伤，则最可能损伤部位将位于模态应变能密度差值最大处，空间网架损伤识别时，绘制损伤识别指标单元模态应变能密度差MSEDC随单元变化的柱状图，柱状图中最大处或者比较大处将被认为是损伤的位置。

2 有限元算例分析

2.1 结构模型建立

算例采用如图1所示的空间网架结构模型，其跨度为10 m，高为1 m，上下弦杆均长2 m，所有杆单元截面面积为A=4 560 mm2，其力学参数弹性模量为E=2.06×1011 Pa，材料密度为ρ=7 850 kg/m3，泊松比μ=0.3，上弦5跨，下弦4跨，共20个支座。为了便于分析，每根杆件划分为1个单元，共200个杆单元，61个节点。利用ANSYS建模，并采用ANSYS的APDL语言编程求解，采用LINK8模拟空间网架杆件，每个节点只有3个线位移自由度，杆件只承受轴力，四角点支座为三向约束，其他支座只约束竖向和切向方向。假设结构损伤不引起质量改变，以弹性模量E的下降模拟损伤，且忽略阻尼的影响。考虑结构的5种损伤情况（见表1），分别为上弦杆单损伤、下弦杆单损伤、腹杆单损伤、上下弦杆同时损伤及3根杆件同时损伤等5种工况，计算得到不同工况下的一阶模态参数，然后通过Matlab编制相应的程序，利用单元模态应变能密度差值作为损伤指标，对5种工况下的损伤情况进行识别。计算一阶模态下每个单元对应的损

式中：φij和φzij分别表示加噪声前后的振型;φmax，j表示第j阶振型的最大值;randn表示均值为零、标准差为1的高斯白噪声;β表示实际测量中不同振型的噪声水平。

2.2 结果分析

2.2.1 单杆件损伤位置识别

针对1个单元损伤的情况，分别考虑3种工况：工况1为上弦杆单元45损伤20%、工况2为下弦杆单元98损伤10%、工况3为腹杆121损伤50%，考虑无噪音、5%噪音2种情况，单元一阶模态应变能密度变化曲线见图2—图4。可知：1）当单元发生损伤时，非损伤单元的模态应变能密度差值变化比较小，而模态应变能密度差值变化在损伤单元处急剧增加;2）未加噪、加噪5%检测结果差别很小，

其中单元45加噪5%和未加噪的损伤指标只有02%的误差，单元121的误差最大，为6.9%，但也不影响检测结果，说明模态应变能密度差值作为损伤检测指标具有较好的鲁棒性。

2.2.2 多杆件损伤位置识别

針对多个单元损伤的情况，考虑2种工况，即同时损伤2根杆件的工况4和同时损伤3根杆件的工况5，分别考虑未加噪、加噪5% 2种情形。单元一阶模态应变能密度差值变化曲线见图5、图6。

由图5、图6可知：1）当多单元同时发生损伤时，非损伤单元的模态应变能密度差值变化比较小，而模态应变能密度差值变化在损伤单元处急剧增加，可以准确进行损伤定位;2）未加噪、加噪5%时的检测结果差别很小，不影响检测结果，表明模态应变能密度差值作为检测指标检测多损伤具有较好的鲁棒性。

2.3 模态应变能密度差值对单元损伤程度的识别

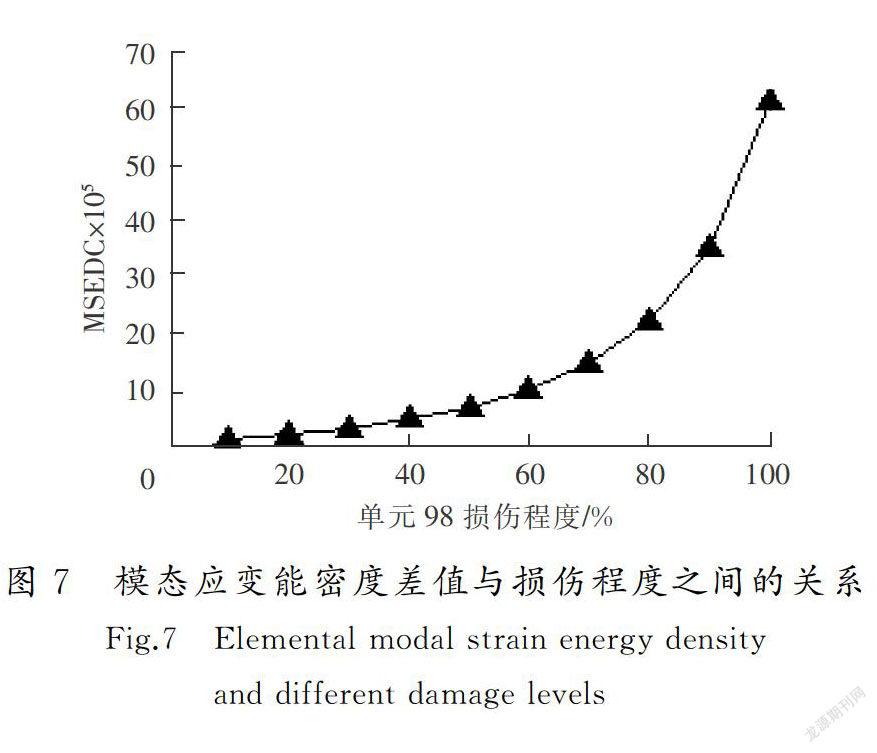
当确定损伤位置后，根据损伤单元的模态应变能密度差值的大小来判断单元的损伤程度，以下弦杆单元98为例，计算并绘制出损伤单元98的一阶模态应变能密度差值大小与损伤程度之间的关系，如图7所示，可以看出，随着网架下弦杆98单元损伤程度的增加，一阶模态应变能密度差值也随之增大，且损

伤程度越大，损伤单元的模态应变能密度差值越大，损伤程度越小，损伤单元模态应变能密度差值越小。根据这一规律，在确定损伤位置后，可根据单元模态应变能密度差值的大小判断单元的损伤程度。

3 结 论

建立了一种基于模态应变能密度的空间网架结构损伤定位方法，根据空间网架结构杆件的受力特点，利用低阶单元模态应变，将空间网架结构在低阶模态下的单元模态应变能密度差值作为结构损伤定位的动力指纹。通过对空间网架结构损伤的数值模拟研究，得出如下结论。

1） 从损伤定位来看，模态应变能密度差值作为空间网架结构损伤的定位指标，能够在一阶模态下，使单损伤、多损伤的定位得到很好的效果。

2）模态应变能密度差值作为损伤指标，不但可以对较严重的局部损伤具有较精确的识别能力，对轻微损伤同样可以有很好的识别能力，这对空间网架结构的早期损伤诊断具有一定的现实意义。

3） 从损伤程度评估来看，单杆损伤可以根据模态应变能密度差值的大小来判断损伤的程度。

4） 模态应变能密度理论应用于空间网架结构损伤识别时，在一定噪声水平下具有较强的鲁棒性，适用于实际工程检测条件的网架损伤诊断。

5） 实际应用中，由于空间网架结构的自由度数量非常多，测量自由度不足时，可用振型扩充法进行扩充。

本文仅研究了数值仿真模拟，未对实际结构的有效性、可靠性进行实验检验，后续将对实际网架结构进行实验研究。

参考文献/References：

[1] SHI Z Y， LAW S S， ZHANG L M. Structural damage localization from modal strain energy change[J]. Journal of Sound and Vibration， 1998， 218（5）： 825-844.

[2] SHI Z Y， LAW S S， ZHANG L M. Improved damage quantification from elemental modal strain energy change [J]. Journal of Engineering Mechanics-Asce， 2002， 128（5）： 521-529.

[3]  HA X.Vibration-based Damage Identification and Health Monitoring of Civil Structures[D].San Diego： University of California，2008.

[4] 林友新，周翠，李宏男，等.单元模态应变能法在输电铁塔损识别中的应用[J].防災减灾工程学报，2013，33（1）：102-107.

LIN Youxin， ZHOU Cui，LI Hongnan，et al.Application of element modal strain energy method in damage identification of transmission tower [J]. Journal of Disaster Prevention and Mitigation Engineering， 2013，33（1）：102-107.

[5]  严平，李胡生，葛继平，等.基于模态应变能和小波变换的结构损伤识别研究[J]. 振动与冲击，2012， 31（1）： 121-126.

YAN Ping，LI Husheng，GE Jiping，et al. Structural damage identification based on modal strain energy and wavelet transformation[J].Journal of Vibration and Shock，2012， 31（1）：121-126.

[6]  颜王吉，任伟新.基于代数算法的单元模态应变能灵敏度分析[J]. 振动与冲击，2010， 29（4）：34-39.

YAN Wangji，REN Weixin.Element modal strain energy sensitivity analysis based on an efficiental gebraic method [J].Journal of Vibration and Shock，2010， 29（4）：34-39.

[7]  WEI Fan， PI Zhongqiao. A strain energy-based damage severity correction factor method for damage identification in plate-type structures [J].Mechanical Systems and Signal Processing， 2012 （28）： 660-678.

[8] 张效忠，姚文娟.敏感模态单元应变能法结构损伤识别[J].中南大学学报（自然科学版），2013，44（7）：3014-3023.

ZHANG Xiaozhong，YAO Wenjuan.Structural damage identification using element strain energy method based on sensitive modals[J].Journal of Central South University （Science and Technology）， 2013，44（7）：3014-3023.

[9] 李永梅，高向宇，史升炎，等.基于单元应变模态差的网架结构损伤诊断研究[J].建筑结构学报，2009，30（3）：152-159.

LI Yongmei，GAO Xiangyu，SHI Shengyan， et al.Damage diagnosis of space truss based on change of elemental strain modal[J].Journal of Building Structures，2009，30（3）：152-159.

[10]宋玉普，刘志鑫，纪卫红.基于模态应变能与神经网络的钢网架损伤检测方法 [J]. 土木工程学报，2007（10）：13-18.

SONG Yupu， LIU Zhixin， JI Weihong. Damage diagnosis of spatial trusses based on modal strain energy and neural network[J]. China Civil Engineering Journal， 2007（10）：13-18.

[11] 王孟鸿，宋春月，姬晨濛.基于频响函数与主成分分析的网架结构损伤检测方法研究[J].建筑结构，2017，47（4）：96-101.

WANG Menghong， SONG Chunyue， JI Chenmeng. Research on damage detection method for grid structures based on frequency response function and principal component analysis [J].Building Structure， 2017，47（4）：96-101.

[12]張丽梅，刘卫然，张立伟，等.基于单元应变模态差和RBF神经网络的网架损伤检测方法[J]. 河北科技大学学报， 2013， 34（1）：79-85.

ZHANG Limei， LIU Weiran，ZHANG Liwei，et al. Damage testing method of space truss based on elemental strain mode difference and RBF neural network[J]. Journal of Hebei University of Science and Technology，2013， 34（1）：79-85.

[13]范梦，张丽梅.基于曲率模态差和小波变换的网架损伤识别[J]. 河北科技大学学报， 2014， 35（4）：384-391.

FAN Meng， ZHANG Limei. Grid damage detection based on curvature mode difference and wavelet transform [J]. Journal of Hebei University of Science and Technology， 2014， 35（4）：384-391.

[14]张丽梅，燕静静，杜守军，等.基于欧氏距离的网架单点最优激励位置研究 [J]. 河北科技大学学报， 2014， 37（5）：119-123.

ZHANG Limei， YAN Jingjing， DU Shoujun，et al. Study of single optimal excitation position based on euclidean distance in spatial truss structure[J].Journal of Hebei University of Science and Technology， 2014， 37（5）：119-123.

[15]曹晖，林秀萍.结构损伤识别中噪声的模拟[J].振动与冲击， 2010， 29（5）：106-109.

CAO Hui， LIN Xiuping.Noise simulation in structal damage identification[J]. Journal of Vibration and Shock，2010， 29（5）：106-109.