分数阶统计分布与金融投资①

王治力 陈秋同 王俊杰

摘 要：在金融投资领域，常会遇到根据历史行情对未来行情走势进行预测的问题，对此本文通过样本总体分布判断，建立Lévy稳定分布决策模型拟合数据，求解分布统计量。根据分布统计量求解金融投资的两大重要参数，最终得到企业金融投资决策问题的一类优选方法。

关键词：Lévy稳定分布 置信区间 金融投资 正态分布

中图分类号：F832 文献标识码：A 文章编号：2096-0298（2018）12（b）-051-02

1 分数阶统计分布简介

分数阶统计分布及其随机过程是一类广泛应用于描述非高斯变量和非马尔科夫过程的统计方法。Lévy稳定分布是一种具有幂律特征的分数阶统计分布，其概率密度或累计分布曲线表现为尖峰拖尾特征，尾部为幂律衰减，对应的随机过程可以描述长程相关性和突发性。1963年Mandelbrot首次将其用于金融领域。

2 问题引入

金融市场与一般商品市场的根本区别在于它的收益的不确定性，在日趋复杂的市场条件下，想要在变幻莫测的金融市场中作出合理的、科学的决策，采用合理的数学方法，从经验投资向科学投资发展至关重要。

现有一公司欲拿出1000万元流动资金进行股票投资，该公司在过去的255个股票交易日中的日收益额（如表1所示）。该公司打算根据上述历史行情进行决策，其中日均十万元损失率与置信度95%的日均损失额为两个重要的参考指标。本文使用分数阶统计分布方法对该问题进行求解。

3 模型假设

（1）假定表1中的数据为每天结算一次且保持每天在市场上的投资额为1000万元。

（2）由于市场受众多随机因素影响，因此认为每天公司收益额数据之间相关性极弱，近似认为相互独立。

（3）所给数据具有真实性、代表性、可靠性。即忽略统计误差，排除人为因素，认为此数据是正常市场投资的结果。

4 模型的求解

4.1 基于分数阶统计分布的投资决策模型

Lévy稳定分布是一类分数阶统计分布，该分布的概率密度函数具有尖峰、非对称、拖尾特征。刻画此类分布需要四个参数，分别是稳定系数α、倾斜指数β、尺度参数γ和位置参数δ，参数的取值范围分别为：

0≤α≤2，-1≤β≤1，γ>0，δ∈R。

正态分布和柯西分布是其稳定指数等于2和1时的特殊情形。

Lévy稳定分布倾斜指数能够刻画收益额統计分布的拖尾特征，为研究金融投资收益额的统计分布提供了一种更为优良的方法。

此外，由于Lévy稳定分布的概率密度函数和累积分布函数均没有统一的解析表达式，因此，采用合适的软件工具十分必要，本文利用一种Lévy稳定分布软件工具包及相关程序实现分布统计量的计算。

4.2 Lévy稳定分布参数计算

为了刻画Lévy稳定分布，首先需要计算Lévy稳定分布的四个参数，利用经验特征函数法估计收益额样本对应的Lévy稳定分布参数（如表2所示）。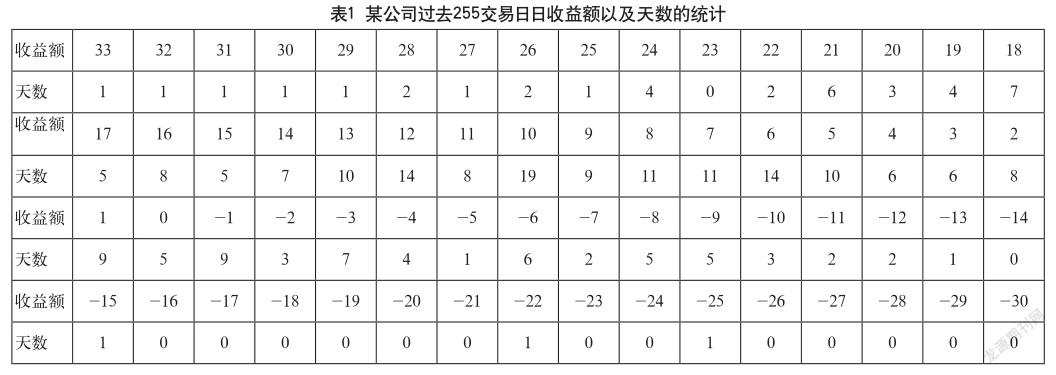

对得到的标准Lévy模型做进一步分析，对样本数据与Lévy随机数做K-S检验，得到显著性水平值为0.3921（置信水平为0.05），接受原假设H0，即样本数据满足Lévy总体分布。对比正态总体的K-S检验水平0.028，易知Lévy稳定分布相比高斯分布更适合该投资决策模型。

类似的，利用经验特征函数法，结合CMS生成的Lévy随机数作为标准模型求出对应的统计参数。值得说明的是，一般有两种方法可以求解分布函数：经验特征函数法与百分位法，后者具有更高的计算效率，但误差稍大，因此本模型中均选取经验特征函数法计算分布函数。表3是两种方法求得的Lévy稳定分布统计量与标准Lévy分布的对比。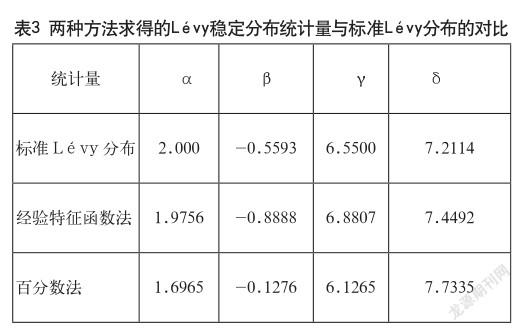

图1是样本累积分布函数与Lévy累积分布函数图，样本拟合得到的经验分布函数与标准Lévy曲线基本重合，可见用Lévy稳定分布来模拟金融投资行为是较为可靠的。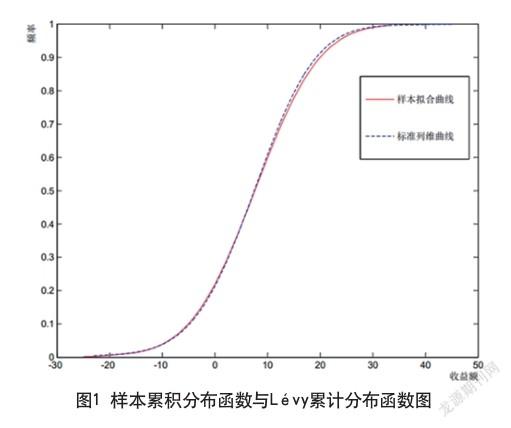

4.3 模型求解

通过MATLAB使用多项式函数拟合样条曲线，可以得到9次拟合多项式约为（由于matlab只能得到各系数取值的置信区间，本文中多项式各系数为置信区间中值）：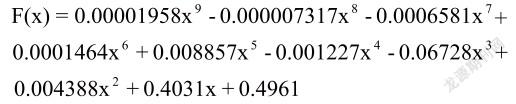

则下一交易日的日均十万元损失率为：P （ x < -10）=F（-10）=0.03944，故而下一周期损失超过十万元的概率为3.944%。置信度95%的日均损失额为F-1（0.05）=8.8185，故而在95%置信度下损失不超过8.8185万元。

5 模型分析与推广

本文通过Lévy稳定分布模型对金融投资中的重要参数进行估计，由于本问题的日收益样本概率密度函数具有尖峰拖尾特征，故从理论上分析，采用Lévy稳定分布可以得到较高斯分布更为优化的结果。本文中通过对Lévy稳定分布进行K-S检验，发现Lévy稳定分布的显著性水平低于正态分布，证明了Lévy稳定分布在金融投资问题解决中的优越性。除了金融投资之外，Lévy稳定分布模型还广泛应用于反常扩散，信号处理等领域。

参考文献

[1] 徐成贤，林卫东.数学与现代金融投资理论[J].西安交通大学学报（社会科学版），1998（3）.

[2] 印凡成，夏乐天.概率论与数理统计[M].南京：河海大学出版社，2000.

[3] 陈文.力学与工程问题的分数阶导数建模[M].北京：科学出版社，2010.

[4] Kozubowski T J. The inner characterization of geometric stable laws[J].Statistics &Decisions，1994，12（3）.

[5] Weron R. Computationally intensive value at riskcalculations [M].Gentle J E， H rdle W， Mori Y， eds.Handbook of Computational Statistics. Berlin： Springer，2004.

[6] 梁英杰，陈文.Lévy稳定分布对住宅楼面活荷载的统计分析[J].工程力学，2014，31（6）.

①基金项目：“江苏高校品牌专业建设工程资助项目”（英文标志：Top-notch Academic Programs Project of Jiangsu Higher Education Institutions，简称：TAPP）。