航天器平移及姿态机动自适应终端滑模控制*
岳宝增 李晓玉
(北京理工大学 宇航学院, 北京 100081)
引言
现代航天器大角度姿态机动及轨道机动往往是以六个自由度的平动及姿态运动建模.此时系统的非线性运动方程中六个自由度的平动和旋转运动是动态耦合、高度非线性的. 而且,未知的环境力矩会对航天器产生外部扰动,机动时的燃料晃动和消耗会使航天器的惯性矩阵和质量特性发生变化,导致参数不确定.因此,控制系统应该能够考虑外部干扰并适应质量分布的变化[1-3].
自适应控制器能够修正自身特性以适应运动及扰动动态特性变化[4].由于现代航天器控制系统存在参数不确定及外部干扰,因而自适应控制器具有重要的实际意义.许多应用中(如轨道和大角度机动),航天器的惯性矩阵可能存在较大的模型误差,因此提出了自适应控制.机动过程中,系统的惯量矩阵将由于燃料消耗(或者燃料晃动及流体结构耦合动力学[1-3])或部件连接的改变而发生变化,因此控制器的设计必须有效克服这种变化对航天器的影响.自适应反馈控制可以解释并解决航天器跟踪目标轨道的问题[3].由于控制律具有六阶动态补偿器形式,因而无需知道航天器惯量或者质心位置.文献[5]研究了具有惯性不确定性及外部干扰的非线性航天器系统的姿态稳定问题.在应用滑模控制器控制闭环系统的状态变量时,需要自适应律预估干扰.对具有执行偏差及质量未知的刚体航天器整体平移及旋转的有限时间控制问题采用了反演鲁棒自适应控制方法[6].
本文对航天器的耦合平移及姿态动力学进行了动力学和运动学描述,并将无奇异问题的四元数用于姿态运动学.应用自适应终端滑模控制器驱动航天器在有限时间内(非渐进式)到达目标轨道.所提出的设计方案具有快速机动响应性,并且对于模型的不确定性及环境扰动具有很好的鲁棒性.利用李雅普诺夫稳定性理论证明了控制器的可达性及稳定性.最后通过数值仿真验证了控制器的效率和准确性.
1 航天器耦合平移及姿态动力学方程
首先根据所要建立的耦合动力学模型选择坐标系,如图1所示.直角坐标系EXIYIZI为原点在E点的惯性参考系.直角坐标系OXsYsZs为固定在航天器刚体上的随体坐标系,其原点为主刚体质心,R是在坐标系EXIYIZI中所表示的从E到O的矢径.参考坐标系下的航天器姿态是由方向余弦矩阵或者欧拉角定义的.本文中,欧拉角被定义为关于刚体轴的旋转角,其中:θx,θy,θz分别是绕轴Xs,Ys,Zs的旋转角.坐标系变换矩阵按照OXs→OYs→OZs的顺序.因而得到坐标系EXIYIZI和OXsYsZs的坐标系变换矩阵为:
(1)
(2)
其中:sk=sinθk,ck=cosθk.自由指标k表示固定于主刚体的坐标.
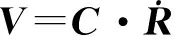
(3)
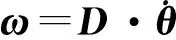
(4)
V,ω分别是航天器相对于惯性系的速度和角速度(角速度表示为准坐标的时间导数以及坐标转化矩阵的积).

图1 航天器系统的示意图Fig.1 Schematic representation of the spacecraft system
根据一般准坐标系下的拉格朗日方程,得到航天器六自由度平移和姿态运动的动力学方程[7].
(5)
(6)
L表示拉格朗日函数.f和u分别是控制力和力矩.df和du分别是外部干扰力和力矩.符号×表示作用于向量ω=[ωxωyωz]T的运算:
方程(5)和(6)可以写成如下形式:
(7)
(8)
m和J分别为主刚体的质量和惯性矩阵.耦合系统的状态向量(或广义坐标系)可表示为Z=[Rx,Ry,Rz,θx,θy,θz,vx,vy,vz,ωx,ωy,ωz]T,耦合动力学和运动学方程(3),(4),(5)和(6)可以利用四阶的龙格库塔法联合求解.
方程(3)和方程(4)用欧拉角描述了航天器的姿态动力学方程.欧拉角具有最小尺度的优点,但是存在计算量大及奇异性问题.本文采用四元数对刚体航天器进行了全局姿态描述.欧拉角转换为四元数的关系式如下[8]:
(9)
Sj/2=sin(θj/2),Cj/2=cos(θj/2),j=x,y,z.

(10a)
(10b)
I3是三阶的单位矩阵.因此方程(3),(10),(7)和(8)构成了一组航天器耦合平移及姿态动力学的运动学及动力学方程.
2 航天器平移和姿态机动的控制策略设计
本节所设计的控制器是为航天器在参数不确定性及外部干扰下的运动提供鲁棒自适应控制.控制任务可以简单概述为:对于初始状态R(t0)=R(0)=R0(位置)以及θ(t0)=θ(0)=θ0(姿态)的航天器,所设计的控制律能够驱使闭环耦合的航天器系统在t→T时,状态(3)、(10)、(7)和(8)为零.其中T是收敛时间.可以表示为:
(11)
在给出控制设计之前,首先给出一些与设计控制方法相关的引理.
引理1[10]如果α∈(0,1),那么下列不等式成立:
(12)
引理2[10]对任意实数i=1,…,n,并且0<α<1,下列等式成立:

(13)
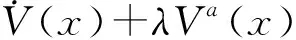
(14)
其中V(x0)是V(x)的初始值.
引理4[12]快速终端滑模形式的有限时间稳定的李雅普诺夫函数展开形式给出如下:
(15a)
(15b)
对于航天器轨道控制,航天器轨道的终端滑模面(或切换面)设为:
S1=CTV+κ1R+κ2sig(R)r
(16)
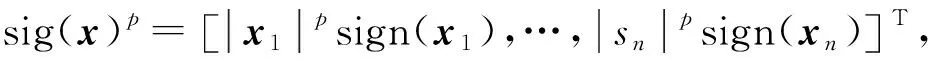
V=C[-κ1R-κ2sig(R)r]
(17)
为证明滑模面的可达性,李雅普诺夫函数为:
(18)
求导得到:
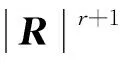

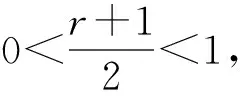
5.控制变量。参考黎文靖和郑曼妮、Tong et al的研究设计,本文在考察政府补贴、研发投入对公司专利申请的影响时,类似地控制了公司规模(Size)、公司年龄(Age)和其他财务指标: 现金流量(CF)、负债比率(LEV)、流动比率(Liquidity)、行业与时间。[4][6]
(19)
定理1由方程(3)、(7)得到的滑模面,控制器(20)能使闭环系统的轨迹在有限时间内达到该滑模面的邻域,并且最终收敛至原点.
f=C[-κ3S1-κ4sig(S1)r]-
(20)
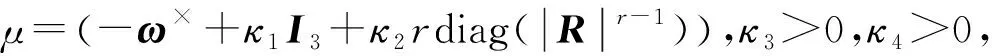
控制器的稳定性证明过程参考文献[13].
类似的,根据引理3,得到航天器轨道终端滑模面由S1(t0)到达S1(t)=0的最长时间为:
(21)
为了抑制控制器的抖振,用饱和函数代替方程(20)的符号函数,控制器转换为:
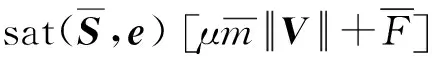
(22)
e=[e1,e2,e3]为约束抖振的符号函数:
(23)
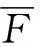
(24)
ζ0>0,ζ1>0.该控制器效率及可行性的证明参考文献[13].该控制方案具有两个特点:(1)控制器不依赖于质量m,因而可以应用于存在多个未知m的航天器系统,并且可以利用自适应方法估计扰动上限.(2)算法计算简单,不包括任何矩阵范数的计算.
由于驱动发动机控制力的大小通常是有限的,为了避免过控制并节约能量,与坐标状态参数增益系数的直接相关量应该大于坐标状态参数间接相关量,即:κ1>κ2,κ3>κ4.此外,当驱动力变化过快时,会引起液体燃料晃动或者挠性附件的振动力,这将会显著影响航天器的姿态和轨道,最终导致航天器控制器失效.因此,所有控制器的增益系数必须选择一些较小的值.
对于考虑惯性不确定性以及外界干扰的航天器姿态控制,根据参考文献[15]最终给出快速终端滑模控制器(AFTSM)如下:
(25)
S=[S2x,S2y,S2z]T∈R3,λ1>0,λ2>0,0
3 数值模拟与讨论
本节对刚体航天器的平移和姿态机动问题进行了仿真,证明了滑模控制器(24)和(25)的作用.在仿真中使用的是文献[5,14]中的航天器模型,其中航天器参数:
航天器机动的初始条件和期望的最终状态如表1所示.

表1 航天器机动的初始状态及目标状态Table 1 The initial conditions and the desired final states for spacecraft maneuvering
给出不确定参数为:
ΔJ=diag[sin(0.1t),2sin(0.2t),3sin(0.3t)]kg·m2
(26)
Δm=5sin(0.5t)kg
(27)
外部干扰力及力矩为:
(28)
(29)
其中,δ(ti,Δti)表示在时间ti开始作用的幅值为1,宽度为Δti秒的脉冲扰动.
数值模拟结果如图2~10所示.航天器的位置及平移速度随时间变化趋势如图2和3所示.航天器欧拉角变随时间变化趋势如图4所示.姿态速度和角的四元素随时间变化趋势如图5和6所示.图7和图8分别显示了航天器平移和机动的控制力和力矩输入.图9和10给出了滑模面随时间变化趋势.
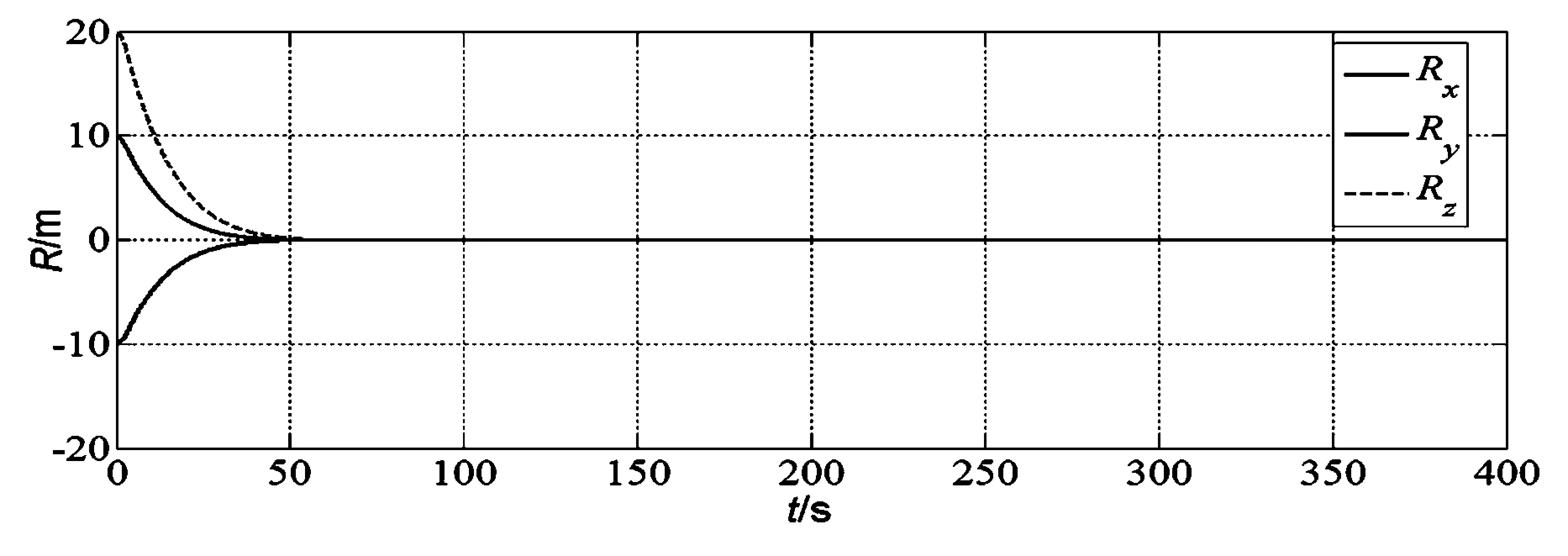
图2 航天器位置随时间变化趋势Fig.2 Time history of position for spacecraft

图3 航天器平移速度随时间变化趋势Fig.3 Time history of translation velocity for spacecraft

图4 航天器欧拉角随时间变化趋势Fig.4 Time history of Euler angles for spacecraft

图5 航天器角速度随时间变化趋势Fig.5 Time history of angular velocity for spacecraft

图6 航天器四元数随时间变化趋势Fig.6 Time history of quaternion for spacecraft

图7 航天器控制力矩输入随时间变化趋势Fig.7 Time history of control torque input for spacecraft
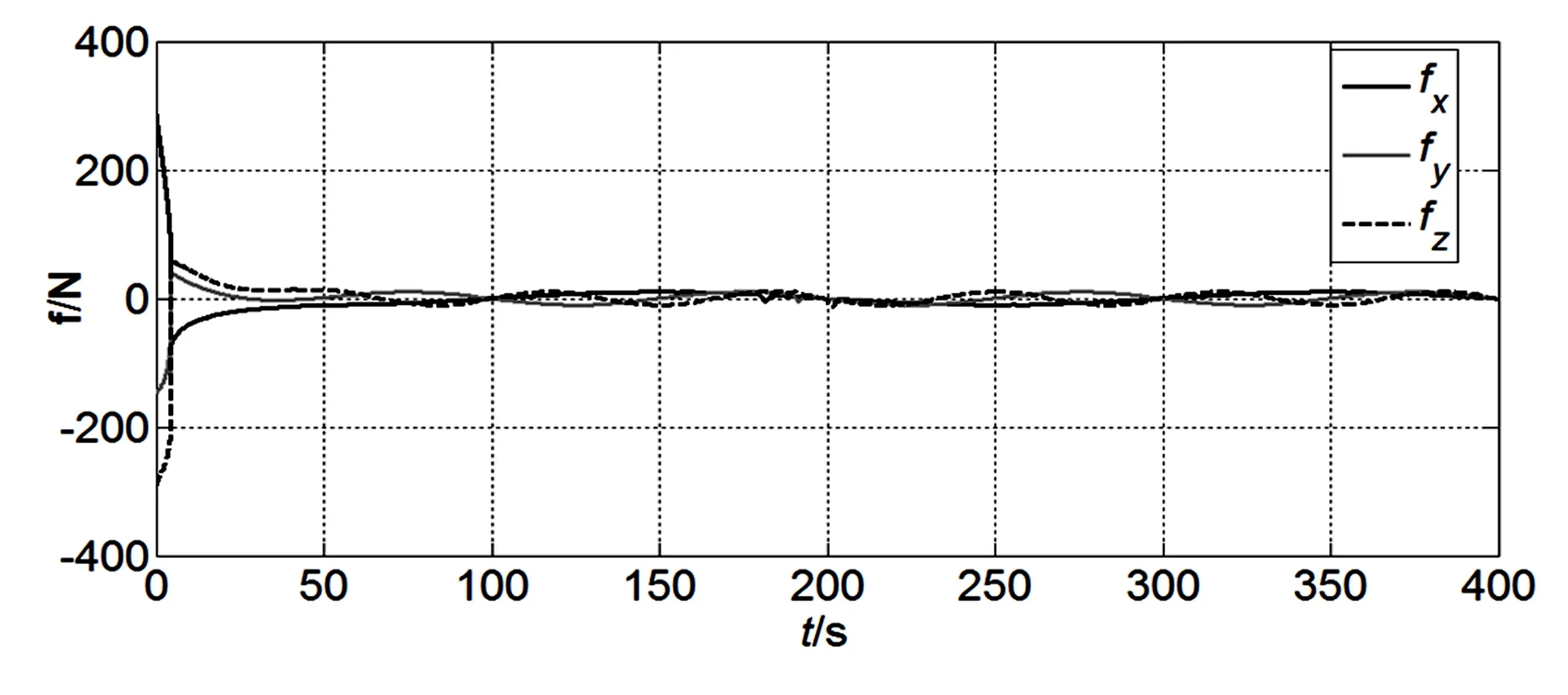
图8 航天器控制力输入随时间变化趋势Fig.8 Time history of control force input for spacecraft
图9 航天器平移控制的滑模面随时间变化趋势Fig.9 Time history of sliding surface for spacecraft translation control
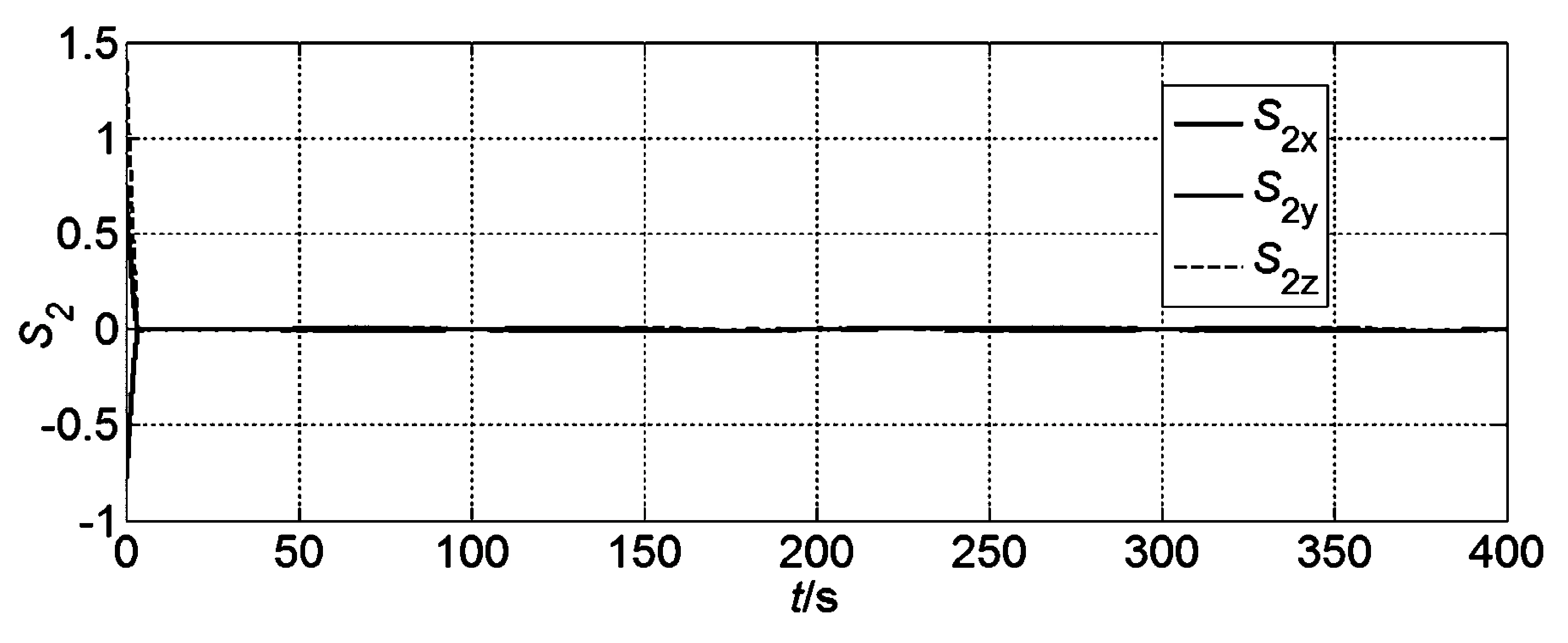
图10 航天器姿态控制的滑模面随时间变化趋势Fig.10 Time history of sliding surface for spacecraft attitude control
如图2、图3所示,50秒后的位置和平移速度收敛到零.图4~6显示35秒后欧拉角,角速度及四元数收敛到零.外部干扰和惯性不确定性的影响已被有效地抑制并且轨迹是光滑的.根据图7和图8可以得到在180,190和200秒干扰力和力矩的影响.显然所设计的控制器有较好的抗干扰能力.尽管计入了脉冲和正弦干扰,它仍实现了良好的位置和姿态动力学响应.干扰模型(28)和(29)包括正弦脉冲和脉冲干扰.一般情况下,脉冲干扰对系统响应有很大的影响[14].因此,所提出的自适应终端滑模控制有效地抑制了这种干扰在平移和姿态机动中的影响.这也表明所提出的控制器能在t=0时使滑模面几乎同时达到S=0.仿真结果表明本文所设计的控制方案对于航天器的位置和姿态跟踪机动非常有效.
4 结论
本文介绍了自适应终端滑模控制器.它可以用来控制航天器有限时间收敛的平移和姿态机动,并能抑制不必要的抖振.利用控制律预估干扰和惯性的不确定,该控制方案无需知道干扰和惯性矩阵.这种自适应终端滑模控制方法不仅对于参数不确定具有鲁棒性而且具有较好的抗干扰能力.即使考虑脉冲和正弦扰动仍具有良好的位置和姿态动力学响应.通过列举控制具有耦合平移和姿态机动的航天器的例子,给出了控制器的效率和精度,并进行了验证与数值仿真.

