非线性时滞奇异系统的严格实用稳定性研究*

王贵元 杨卓琴

(北京航空航天大学 数学与系统科学学院, 数学，信息与行为科学教育部重点实验室, 北京 100191)

引言

20世纪70年代,英国学者H.H.Rosenbrock提出奇异系统的概念,它是比正常状态系统应用范围更广泛的一类系统,此类系统已在飞行器模型、电路系统等领域有广泛的应用[1,2].到目前为止,关于线性奇异系统已经取得了很多研究成果,其中大多数是研究实用稳定性. 实用稳定性理论是现代运动稳定性理论的研究方向之一,所研究的系统,数学意义上可能是不稳定的,但是在实际问题中是可以接受的[3].因此,从实际的角度可以认为这些系统是稳定的,正因为如此,实用稳定性引起了很多学者的关注,并取得了许多研究成果.文献[4]研究了初始时刻不同的非线性微分方程的实用稳定性,文献[5]讨论了脉冲系统的实用稳定性,利用比较原理得出该类系统实用稳定的充分条件.文献[6]研究了含有时滞的脉冲微分方程的最终实用稳定性,得到了此类方程最终实用稳定的判别准则.

严格实用稳定性是一类可以给出解的衰减速度信息的稳定性[7,8].它与实用稳定性的关系是,某个系统的解是严格实用稳定的,那么它也是实用稳定的,不同点是实用稳定性仅对上界进行了估计,没有对解的下界进行估计,仅仅是单边估计.基于此,Lakshmikantham[7]等提出了严格稳定性的概念,得出微分方程严格实用稳定的若干判据. 随后,Lakshmikantham和Zhang[8]提出了泛函微分系统严格实用稳定的定义,给出泛函微分系统严格实用稳定的充分条件. Zhang 和Sun[9,10]研究了脉冲系统及脉冲泛函微分系统严格实用稳定等问题.Li[11]等研究了非线性脉冲系统的严格实用稳定性.Liu和Yang[12]利用Lyapunov函数法和Razumikhin技巧,得到了脉冲泛函微分方程严格实用稳定的判据.

然而,关于非线性奇异系统稳定性的研究成果较少,本文将严格实用稳定性的概念推广到非线性奇异系统,通过利用两个Lyapunov函数法和比较原理,得出具有控制输入的非线性奇异系统严格(一致)实用稳定及严格(一致)实用渐近稳定的判定定理. 时滞系统普遍存在于自然和工程实际中,是不可忽略的因素,在一些机械设计过程中,如果忽略时滞,就会降低控制效果,甚至会导致失败[13,14].已有结果表明,时滞会使系统产生复杂的动力学行为[13].因此,我们考虑了含有时滞的非线性奇异系统,给出其关于两个测度严格实用稳定的定义,利用上述两种方法,得到了这一类系统严格(一致)实用稳定和严格(一致)实用渐近稳定的判别准则.

1 预备知识

首先考虑时滞为零的非线性奇异系统[2]:

(1)

其中,E∈Rn×n,rankE=r≤n,x∈Rn是状态向量,f(t,u,x)∈C(R+×Rm×Rn,Rn)对所有参数都连续可微,u(t)∈Rm是控制输入[2].

定义1.1[2]控制项u(t)∈Rm被称为可容许的,如果对任何的初始条件Ex0,系统(1)有唯一的无脉冲的解. 所有的容许输入的集合定义为Ω.

假设1[2]对于任何的初始条件Ex0和控制u(t),系统(1)有唯一的解；

假设2[2]集合Ω是非空集合;

假设3[2]零解是系统(1)的平衡点.

令u=a(t,x)∈Ω满足a(t,0)≡0,系统(1)变为:

(2)

为方便应用,给出下面这些符号的定义：

R+=[0,+∞)

K={α∈C(R+,R+)|α(t)严格单增且α(0)=0}

Γ={h∈C(R+×Rn,R+)|infh(t,x)=0}

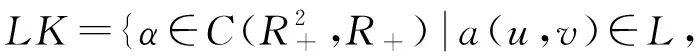
且a(u,v)∈K,∀u}

首先给出非线性奇异系统严格实用稳定的相关定义.

定义1.2称系统(2)的解x(t)=x(t;t0,x0,u*)是:

(1)严格实用稳定的,如果对于给定的(λ1,A1):0<λ1≤A1与某个t0∈R+,可由‖Ex0‖<λ1,得出‖Ex(t)‖λ2,得出‖Ex(t)‖>A2对所有的t≥t0成立；

(2)一致严格实用稳定的,如果对所有的t0∈R+满足定义(1)的条件；

(3)严格吸引的,如果对任意给定的δ1>0,ε1>0与某个t0∈R+,对每个δ2<δ1,存在ε2<ε1,T1=T1(t0,ε1)与T2=T2(t0,ε2),使得当λ2<‖Ex(t0)‖<λ1时,有ε2<‖Ex(t)‖<ε1,对所有的t0+T1≤t≤t0+T2成立；

(4)严格一致吸引的,如果满足条件(3)且T1,T2不依赖于t0；

(5)严格实用渐近稳定的,如果(1),(3)成立,且δ1=λ；

(6)严格一致实用渐近稳定的,如果(2),(4)成立,且δ1=λ.

下面给出比较系统及相关定义.

考虑下列微分系统[2]：

(3a)

(3b)

其中,g1,g2∈C(R+×R+×Rn,R).

定义1.3[8]称比较系统(3)为：

(1)严格实用稳定的,如果对给定的(λ1,A1):0<λ1λ2时,有ω2(t)>A2对所有的t≥t0成立；

(2)严格一致实用稳定的,如果(1)对所有的t0∈R+都成立；

(3)严格吸引的,如果对给定的δ1>0,ε1>0,与某个t0∈R+,对每个δ2<δ1,存在ε2<ε1,T1=T1(t0,ε1)与T2=T2(t0,ε2),使得当ω10<δ时,有ω1(t)<ε1,且当ω20>δ2时,有ω2(t)>ε2,对所有的t0+T1≤t≤t0+T2成立；

(4)严格一致吸引的,如果T1,T2不依赖于t0；

(5)严格实用渐近稳定的,如果(1),(3)成立,且δ1=λ1；

(6)严格一致实用渐近稳定的,如果(2),(4)成立,且δ1=λ1.

注：(1)和(3)或者(2)和(4)不同时成立.

关于含有时滞的非线性奇异系统的相关定义.

考虑下面的奇异系统[2]：

(4)

其中,E∈Rn×n,rankE=r≤n,

xt(θ)=x(t+θ),θ∈[-τ,0],τ>0,x∈Rn

f∈C(R+×Rn×ξ,Rn),f(t,0,0)≡0,t≥t0≥0

系统(4)的初始条件为xt0=φ,φ∈ξ.

令Sk(t0)表示过初始时刻t0的所有初始函数的集合[2],∀φ∈Sk(t0),过点(t0,φ)至少存在一个连续解[2],其中t∈[t0-τ,+∞).

定义1.4[2]令h0∈Γτ,φ∈ξ,对于任意的t∈R+,定义：

定义1.5[2]令h0∈Γτ,h∈Γ,φ∈Sk(t0),称系统(4)的解是：

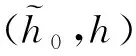
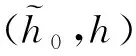
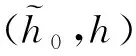
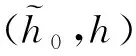
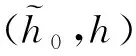
(6) 一致吸引的,如果(5)对于任意的t0∈R+都成立；

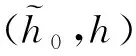
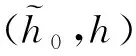
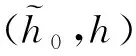
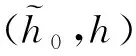
引理1.1[2]

令y=Ex,V(t,y)∈C(R+×Rn,R+)关于y满足局部Lipschitz条件,V(t,y(t))沿着系统(1)的Dini导数定义为：

注：本文均假设V(t,y(t))关于y满足局部Lipschitz条件.

下面给出两个比较原理.

引理1.2[2,8]假设下列条件成立：

(1)存在V∈C(R+×Rn,R+),V(t,y)关于y满足局部李氏条件,其中y=Ex；

(2)存在g1∈C(R+×R+×Rn,R)使得D+V≤g1(t,V(t,Ex),x),∀(t,x)∈R+×Rn,其中x(t)=x(t;t0,x0,u*)是系统(1)的任何一个解；

(3)r(t;t0,ω0,x0,u*)是比较系统:

(5)

的最大解.则当V(t0,Ex0)≤ω10时,有:

V(t,Ex)≤r(t;t0,ω0,x0,u*),∀t≥t0.

另一方面,若D-V≥g2(t,V(t,Ex),x),ρ(t;t0,ω0,x0,u*)是比较系统：

的最小解.则当V(t0,Ex0)≥ω20时,有：

V(t,Ex)≥ρ(t;t0,ω0,x0,u*),∀t≥t0.

引理1.3[8]假设：

(1)u∈C(R+,R+)且D+u≤g(t,u)；

(3)r(t)是比较系统.

的最大解,则当u(t0)≤v(t0)=v0时u(t)≤v(t),t≥t0.

相反,当D-u≥g(t,u),t≥t0,ρ(t)是(A)式的最小解,则当u(t0)≥v0,有u(t)≥ρ(t),t≥t0.

2 主要结果

定理2.1假设：

(1)对给定的(λ1,A1):0<λ1

β1(‖Ex‖)≤V1(t,Ex)≤α1(‖Ex‖)

其中α1,β1∈K并且存在u*=a(t,x)∈Ω,使得：

D+V1≤g1(t,V1(t,Ex),x)；

(2)存在V2(t,Ex)满足：

β2(‖Ex‖)≤V2(t,Ex)≤α2(‖Ex‖)

其中α2,β2∈K且：

D-V2≥g2(t,V2(t,Ex),x)

这里g1,g2∈C(R+×R+×Rn,R).

则比较系统(3)的解严格实用稳定蕴含系统(2)的解严格实用稳定.

证明系统(3)是严格实用稳定的,即存在(λ1,A1):0<λ1β2(λ2)时,ω2(t)>α2(A2), 对所有的t≥t0成立.

只须证,当：

‖Ex0‖<λ1时,‖Ex(t)‖

(6)

假设不成立,即存在t1,t2,使得：‖Ex(t1)‖=λ1,‖Ex(t2)‖=A1,λ1≤‖Ex(t)‖≤A1,t∈[t1,t2].

由条件(1)可得：

β1(A1) =β1(‖Ex(t2)‖)≤V1(t2,Ex(t2))

≤r(t2,t1,ω(t1),x(t1),u*)

<β1(A1)

矛盾,所以(6)式成立；

另一方面,只须证明：

‖Ex0‖>λ2时,‖Ex(t)‖>A2

(7)

反证法,假设结论不成立,即当满足‖Ex0‖>λ2时,存在t1使得：

‖Ex(t1)‖=A2,A2≤‖Ex(t)‖≤A1,t∈[t0,t1].

利用条件(2)和引理1.2得：

α2(A2) =α2(‖Ex(t1)‖)≥V2(t1,Ex(t1))

≥ρ(t1,t0,ω(t0),x0,u*)>α(A2)

矛盾,所以(7)式成立.故系统(2)的解是严格实用稳定的.

类似地,可以得出如下定理.

定理2.2如果定理2.1中的条件(1),(2)都成立,且比较系统(3)严格一致实用渐近稳定,则系统(2)的解是严格一致实用渐近稳定的.

定理2.3假设：

(1)对给定的(λ1,A1):0<λ1

α1∈LK,β1∈K,V1(t,Ex),∀(t,Ex)∈R+×S(ρ)

使得：

α1(t0,λ1)<β1(A1)

β1(‖Ex‖)≤V1(t,Ex)≤α1(t0,‖Ex‖)

并且存在u*=a(t,x)∈Ω使得D+V1≤0,t∈R+；

(2)存在V2(t,Ex),α2∈LK,β2∈K,使得：

β2(‖Ex‖)≤V2(t,Ex)≤α2(t0,‖Ex‖)

且满足：

D-V2≥0,α2(t0,A2)<β2(λ2)

则称系统(2)的解是严格实用稳定的.

证明对给定的(λ1,A1):0<λ1≤A1<ρ,使得当：

‖Ex0‖<λ1时,‖Ex(t)‖

(8)

若结论不成立,即∃t1,t2,使得当：

‖Ex(t1)‖=λ1,‖Ex(t2)‖=A1

λ1≤‖Ex(t)‖≤A1,t1≤t≤t2

时,由条件(1)得：

β1(A1) =β1(‖Ex(t2)‖)≤V1(t2,Ex(t2))

≤V1(t1,Ex(t1))≤α1(t1,Ex(t1))

≤α1(t0,λ1)

又因为：

α1(t0,λ1)<β1(A1)

矛盾,(8)式成立；

另一方面,只须证明对任何λ2<λ1,存在A2<λ2,使得当0

λ2<‖Ex0‖<λ1⟹A2<‖Ex(t)‖

(9)

若结论不成立,即存在t1,t2使得：

‖Ex(t2)‖=λ2,‖Ex(t1)‖=A2,

A2≤‖Ex(t)‖≤λ2,t0

由条件(2)可得：

α2(t0,A2) ≥α2(t1,A2)=α2(t1,‖Ex(t1)‖)

≥V2(t1,Ex(t1))≥V2(t2,Ex(t2))

>β2(λ2)

因为：

α2(t0,A2)<β2(λ2)

矛盾,因此(9)式成立.因此系统(2)的解是严格实用稳定的.

推论2.1如果定理2.3中的α1(t0,‖Ex‖),α2(t0,‖Ex‖)分别用α1(‖Ex‖)和α2(‖Ex‖)来代替,其它条件不变, 则系统(2)的解是严格一致实用稳定的.

推论2.1证明的过程类似定理2.3,详细证明过程从略.

定理2.4假设：

(1)对给定的(λ,A):0<λ

(2)h0∈Γτ,h∈Γ且存在ψ∈LK使得：

(3)如果存在：

V1:R+×S(h,ρ)→R+,α1∈LK,β1∈K

使得当(t,x)∈R+×S(h,ρ)时,有：

D+V1(t,x)≤0

(4)如果存在：

V2:R+×S(h,ρ)→R+,α2∈LK,β2∈K

使得当(t,x)∈R+×S(h,ρ)时,有：

D-V2(t,x)≥0

(5)ψ(t0,λ)

设x(t,t0,φ)是系统(4)的解,由条件(3)可得：

β1(h(t,x)) ≤V1(t,x)≤V1(t0,φ)

≤α1(t0,λ)<β1(A)

(10)

所以,h(t,x)

≤α2(t0,h(t0,φ))≤α2(t0,B)

矛盾,所以h(t0,φ)>B.

≤V2(t1,x(t1))≤α2(t1,h(x(t1)))

≤α2(t1,B)≤α2(t0,B)<β2(η)

(11)

下面给出定理2.4的特殊情况.

下面引入比较系统,通过借助比较系统,研究非线性奇异时滞系统的严格实用稳定性[7].

(12a)

(12b)

比较系统(12)严格实用稳定性的定义与比较系统(3)类似,详见文献[8],此处省略.

定理2.5假设：

(1)对给定的(λ,A):0<λ

(2)h0∈Γτ,h∈Γ且存在ψ∈LK使得：

(3)如果存在：

V1:R+×S(h,ρ)→R+,α1∈LK,β1∈K

对任意的(t,x)∈R+×S(h,ρ)时,有：

和

D+V1(t,x)≤g1(t,V1(t,x))

(4)如果存在：

V2:R+×S(h,ρ)→R+,α2∈LK,β2∈K

对任意的(t,x)∈R+×S(h,ρ)时,有：

和

D-V2(t,x)≥g2(t,V2(t,x))

(5)ψ(t0,λ)

证明比较系统(12)严格实用稳定,则对于给定的(λ,A),0<λ0使得u20>η时,有u2(t)>B,对所有的t≥t0成立.

r(t,t0,u1(t0))<β1(A),∀t≥t0,

其中r(t,t0,u1(t0))是比较系统(12a)的最大解,由条件(3)及引理1.3可得：

V1(t,x(t))≤r(t,t0,u10),∀t≥t0

β1(h(t,x))≤V1(t,x)≤r(t,t0,u10)<β1(A)

(13)

另一方面,对于任何η<λ存在B<η,使得当u20>β2(η)时,u2(t,t0)>α2(B),只须证明,

(14)

h(t1,x(t1))=B,h(t,x(t))>B(t0≤t

利用条件(4)和引理1.3得：

α2(B) =α2(h(t1,x(t1)))≥V2(t1,x(t1))

≥ρ(t1,t0,u2(t0))>α2(B)

定理2.6假设：

(1) 对给定的(λ,A):0<λ

(2)h0∈Γτ,h∈Γ且存在ψ∈LK使得：

(3) 如果存在V1(t,x),α1∈LK,β1∈K,对任意的(t,x)∈R+×S(h,ρ)有：

和

D+V1(t,x)≤g1(t,V1(t,x))；

(4) 如果存在V2(t,x),α2∈LK,β2∈K,对任意的(t,x)∈R+×S(h,ρ)有：

和

D-V2(t,x)≥g2(t,V2(t,x));

(5)ψ(t0,λ)

系统(12)是严格实用渐近稳定的,也是严格吸引的,即给定β1(ε1)>0,对任意的：

α1(λ2)<α1(λ1), ∃T1(t0,ε1),T2(t0,ε2),β1(ε2),β1(ε2)<α1(λ2)使得当β2(λ2)

u1(t,t0,u10) ≤u1(t,t0,α1(λ1))

<β1(ε1),t∈[t0+T1,t0+T2]

u2(t,t0,u20) ≥u2(t,t0,β2(λ2))

>α2(ε2),t∈[t0+T1,t0+T2]

即证：

ε2

h(t0,φ)<ε1,t∈[t0+T1,t0+T2]

由条件(2)得：

其中r(t,t0,u1(t0))是比较系统(12a)的最大解,由条件(3)及引理1.3可得：

V1(t,x(t))≤r(t,t0,u10),∀t≥t0.

β1(h(t,x))≤V1(t,x)≤r(t,t0,u10)<β1(ε1)

另一方面,对于任何λ2<λ1,存在ε2<λ2,使得当u20>β2(λ2)时,u2(t,t0)>α2(ε2), 只须证明：

(15)

h(t1,x(t1))=ε2,h(t,x(t))>ε2(t0≤t

利用条件(4)和比较原理得：

α2(ε2) =α2(h(t1,x(t1)))≥V2(t1,x(t1))

≥ρ(t1,t0,u2(t0))>α2(ε2)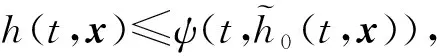

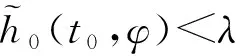
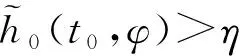
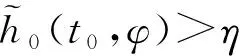
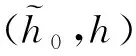
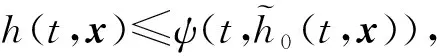
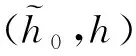
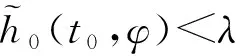
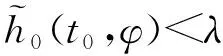
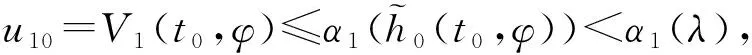
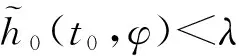
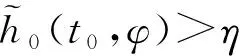
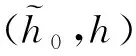
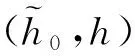
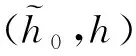
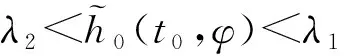
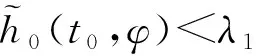
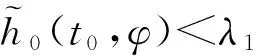
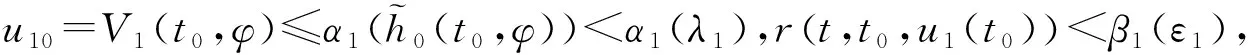
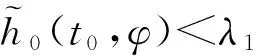
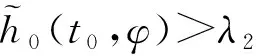
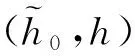
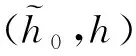
3 小结