基于采样PD反馈的倒立摆控制系统的稳定性*
王强 梁松 王在华,†
(1.解放军陆军工程大学, 南京 211101) (2.南京航空航天大学 机械结构力学及国家重点实验室, 南京 210016)
引言
倒立摆是一个结构简单的力学模型,具有广泛的应用.例如,静止站立的人体[1-4],竖立在手指指尖的火柴棒[1,5],旋转的机器人关节[6]和平衡车[7]等都可以抽象成倒立摆模型.倒立摆系统是开环不稳定的非线性系统,粘性阻尼不能使倒立摆力学系统稳定,可具有复杂的动力学现象.倒立摆系统由于其广泛应用和复杂的动力学特性吸引了众多学者对其进行研究.在倒立摆的镇定控制中,文献[6]使用PD(proportional-derivative)控制器研究了机器人姿态平衡问题,并验证了该控制器对弹性参数及载荷质量均具有很好的鲁棒性.文献[8]在倒立摆系统中使用了多个PID(proportional-integral-derivative)控制器,成功实现了开环系统的稳定控制和轨迹控制,并且控制器对大振幅干扰和高频干扰具有很好的鲁棒性.文献[9]结合经典的LQR(linear quadratic regulator)方法与基因算法给出了控制倒立摆系统的最优控制方法,模拟结果表明,对基因算法求得的最优参数,控制器比经典控制具有更好的控制效果.其它控制手段,如:非线性控制[10]、模糊控制[11]、自动控制[12]等都可实现对倒立摆系统的控制.在控制环节,信息采集、传输、处理以及作动器响应等过程都需要一定时间,不可避免地存在时滞,从而控制系统方程是时滞微分方程.研究表明,对于小时滞,时滞PD控制器能有效地控制倒立摆系统,但是当时滞量超过一个临界值时,时滞PD控制器将不能使倒立摆系统稳定[1,13].如果在时滞PD控制器中增加时滞加速度反馈项,得到时滞PDA(proportional-derivative-acceleration)控制,能有效地增大增益平面稳定性区域的大小[14,15].
数字采样控制是当前控制工程技术领域的一种主流控制技术,它基于计算机完成信号采样、分析、传输,并以离散的数字信号作为控制输入.采样控制是具有分段线性时滞的反馈控制,时滞量和采样周期对控制系统的动力学有重要影响.例如,在研究采样PD控制作用下单自由度振动系统的稳定性时,文献[16]将采样控制中的时滞量从一个采样周期滞后[17]推广到了多个采样周期滞后,理论上说明了随着时滞量的增加,稳定性区域将逐渐减小.文献[18]讨论了位移与速度反馈具有不同时滞时,时滞PD采样控制中不同时滞量组合对一个简单的力控制系统的稳定性区域的影响,与等时滞情形相比较,当位移信号的时滞量两倍于速度信号的时滞量时,在增益参数平面内具有更大的稳定性区域.文献[19]以单自由度系统为研究对象,考虑了速度信号和加速度信号都具有时滞效应的反馈控制,发现时滞加速度信号在采样作用下可以被看作是一种含时滞的参数激励,其能使不稳定系统得到镇定,同时,在一定范围的采样周期下,增大采样周期会使得稳定性区域增大.这表明,采样控制的时滞量与采样周期都可能给系统的稳定性带来复杂的影响.目前,多数文章研究了时滞量对采样控制系统稳定性的影响,少有文章考虑采样周期对稳定性的影响.本文将采样PD反馈控制应用于一个含阻尼的倒立摆系统上,不仅考虑时滞量对系统稳定性的影响,而且考虑采样周期对稳定性区域的影响,以及时滞量和采样周期对收敛速度的影响.
本文第一节给出了采样控制作用下的倒立摆控制系统的运动方程,它是一个微分-差分方程,然后在满足采样定理条件下将其转化为差分方程;第二节基于差分方程研究了采样周期与时滞量对倒立摆系统稳定性区域大小的影响;第三节给出了控制增益的选取方法,使倒立摆控制系统具有最快收敛速度,并且讨论了采样周期与时滞量对收敛速度的影响;第四节为本文的总结.
1 受控倒立摆系统的运动方程
考察图1所示的作平面运动的倒立摆系统,摆长L,质量m,摆的质心距转轴的距离l,摆的转动惯量为J,滑块的质M,滑块与滚轴的摩擦阻力忽略不计,滑块受到水平的控制力Q.设摆杆偏离竖直向上的角度为θ,滑块的水平位移为x.

图1 倒立摆模型Fig.1 Model of an inverted pendulum
(1)
其中,qj为广义坐标,T,V,D和Fqj分别表示系统的动能、势能、耗散能和广义力.图1的倒立摆系统是一个二自由度系统,我们考虑的广义坐标是小车的位移x和摆角θ.注意到:
于是有:
(2)
将(2)式代入(1)中,得倒立摆的运动方程为:
(3)

(4)
在θ=0处进行线性化和无量纲化,得到关于摆角θ满足的二阶微分方程:
(5)

采用等时长的采样,采样周期Δt=ti-ti-1,利用零阶采样保持,具有输入时滞的采样PD反馈控制可表示为:
(6)
其中,t∈[ti,ti+1),ti-m=ti-mΔt,m∈Z+,kp和kd分别表示位移反馈增益和速度反馈增益.

下面考虑受控倒立摆系统在平衡点处的局部稳定性,将(6)式代入(5)式中,得到如下分段线性微分-差分方程:

t∈[ti,ti+1)
(7)
kdy2(ti-m)
其中,t∈[ti,ti+1).再令Y=[y1y2]T,得到受控倒立摆的状态方程:
(8)
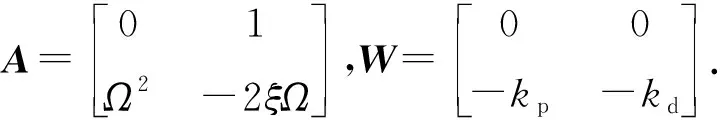
在区间t∈[ti,ti+1)使用常数变易法,得到:
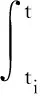
令s=t-τ,有:

将t=ti+1代入上式可以得到采样点之间的关系式:

(9)
由于|A|=-Ω2≠0,从而(9)式右端项可写为:
(10)
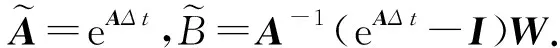
为了计算eAΔt,首先求矩阵AΔt特征值:

进而可得:
将上述结果代入(10),得:
y1(ti+1)=a11y1(ti)+a12y2(ti)+
b11y1(ti-m)+b12y2(ti-m)
y2(ti+1)=a21y1(ti)+a22y2(ti)+
b21y1(ti-m)+b22y2(ti-m)
(11)
其中各系数分别为:
进一步,令:
[z1(ti),…,zm+1(ti),zm+2(ti),…,z2m+2(ti)]T
=[y1(ti),…,y1(ti-m),y2(ti),…,y2(ti-m)]T
=Z(ti)
方程(11)可改写成:
Z(ti+1)=GZ(ti)
(12)
其中,

2 稳定性分析
在满足采样定理条件下,受控倒立摆系统(7)的零解渐近稳定的充分必要条件是差分方程(12)中的系数矩阵G的所有特征值的复数模小于1.下面首先求出矩阵G的特征函数,然后讨论对哪些反馈增益值,其所有零点的模均小于1.
2.1 增益平面的稳定性区域
求矩阵λI-G的行列式的值,将其按第2列和第m+3列进行展开,可得矩阵G的特征函数:
|λI-G|=λ2m+2-β1λ2m+1+β2λ2m-β3λm+1+β4λm+β5
(13)
其中,
β1=a11+a22,β2=a11a22-a12a22,
β3=b11+b22,β4=a11b22+b11a22-a21b12-a12b21,
β5=b11b22-b21b12.
由于|W|=0,所以有:
β5=|A-1(eAΔt-I)W|=0
因而(13)式可化简为|λI-G|=λmpG(λ),其中:
pG(λ)=λm+2-β1λm+1+β2λm-β3λ+β4
(14)
其中的系数可进一步表示为:
=eλ1+λ2=e-2ξΩΔt
方程(12)的稳定性由多项式pG(λ)的零点分布完全确定,进而得到在增益平面上的稳定性区域.
为此考察临界稳定性条件,将λ=±1代入(14)式,得:
因为λ1λ2=-Ω2Δ2t≠0, 所以由pG(±1)=0推出kp=Ω2,此为临界曲线一支.将λ=eiω=cosω+isinω,ω∈(0,π),代入(14)式,分离pG(eiω)的实部与虚部得到:
rp(ω,kp,kd) =R(pG(eiω))
=cos((m+2)ω)-β1cos((m+1)ω)+
β2cos(mω)-β3cosω+β4
ip(ω,kp,kd) =I(pG(eiω))
=sin((m+2)ω)-β1sin((m+1)ω)+
β2sin(mω)-β3sinω
再由关于增益的线性方程组:
(15)
求出(kp,kd)关于ω的参数方程,在参数平面上确定临界曲线的另一支.稳定性区域的边界曲线由临界曲线组成.临界曲线将平面区域划分成多个连通子区域,在每一个连通子区域内,模小于(或大于)1的特征值的个数是相同的,所以,在连通子区域中任意选取一组增益值对应控制系统的稳定性可确定系统在整个子区域内的稳定性.
2.2 采样周期对稳定性区域影响
下列算例中,取ξ=0.1,Ω=1,此时kp=Ω2=1是临界曲线之一.取固定的时滞量mΔt=0.1,不同的采样周期Δt=0.01,0.02,0.05,0.1,即所对应的m=10,5,2,1.下面分别对这4种情况进行讨论.
(1)当Δt=0.01,m=10时,pG(λ)=0化为:
λ12-0.1998×10λ11+0.9980λ10+
(0.4997×10-4kp+0.9990×10-2kd)λ-
0.9990×10-2kd+0.4993×10-4kp=0
(16)
将λ=cosω+isinω代入(16)式,从中可以求得kp,kd关于ω的参数方程.令ω取遍[0,π),即得到临界曲线,如图2所示.在所围成的封闭区域中,取一组参数值(kp,kd)=(30,8),方程(16)的所有复根如表1所示,这12个根的模均小于1,所以系统在临界曲线与临界直线kp=Ω2=1所围成的封闭区域内是渐近稳定的.
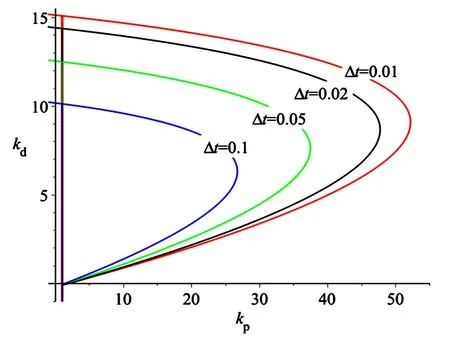
图2 采样周期对稳定性区域的影响,其中τ=0.1Fig.2 Effect of sampling period on the stability region where the delay value is fixed,τ=0.1

root λmodule |λ|0.94170.9417-0.73500.73500.9759±0.9350×10-1i0.98040.6092±0.5318i0.80870.1844±0.7462i0.7686-0.2660±0.6995i0.7484-0.6078±0.4188i0.7381
(2)当Δt=0.02,m=5时,pG(λ)=0化为:
λ7-0.1996×10-1λ6+0.9960×10-1λ5+
(0.1997×10-3kp+0.1996×10-2kd)λ-
0.1996×10-1kd+0.1995×10-3kp=0
(17)
与(1)的方法相同,可画出临界曲线,如图2所示.在所围成的封闭区域中,取一组参数值(kp,kd)=(30,8),方程(17)的所有复根(7个根)的模均小于1,所以系统在临界曲线与临界直线kp=1所围的封闭区域内是渐近稳定的.
(3)当Δt=0.05,m=2时,pG(λ)=0化为:
λ4-0.1993×10λ3+0.9900λ2+
(0.1246×10-2kp+0.4977×10-1kd)λ-
0.4977×10-1kd+0.1242×10-2kp=0
(18)
其临界曲线如图2所示.在所围成的封闭区域中取一组参数值(kp,kd)=(20,8),方程(18)的所有复根的模均小于1,所以系统在临界曲线与临界直线kp=1所围的封闭区域内是渐近稳定的.
(4)当Δt=0.1,m=1时,pG(λ)=0化为:
λ3-0.1990×10λ2+(0.9802+0.4971×10-2kp+
0.9917×10-1kd)λ-0.9917×10-1kd+
0.4938×10-2kp=0
(19)
其临界曲线如图2所示.在所围成的封闭区域中,取一组参数值(kp,kd)=(10,6),方程(19)的所有复根的模均小于1,所以系统在临界曲线与临界直线kp=1所围的封闭区域内是渐近稳定的.
由图2可以看出,对于固定时滞量的系统(7),采样频率越高(采样周期越短),其稳定性区域越大.其原因可能是采样频率越高,采样器在单位时间内获取系统的实时状态信息就越多[18],其更有利于控制系统稳定.
2.3 时滞量对稳定性区域影响
选取固定的采样周期Δt=0.01,不同的时滞量τ=mΔt=0.1,0.11,0.12,0.13,即对应的m=10,11,12,13.其中m=10,已在前一节讨论过,对于m=11,12,13,使用同样的分析方法可以得到渐近稳定区域,其结果如图3所示.

图3 时滞量对稳定区域的影响,其中Δt=0.01Fig.3 Influence of time delay on stable region with sampling period where Δt=0.01
由图3可以看出,对于固定采样周期的系统(7),稳定性区域的大小对时滞量的变化非常敏感:时滞量的小改变,会导致稳定性区域的大变化.
3 最优反馈增益
令向量e(k)=Z*-Z(tk)表示迭代公式(12)的第k步的状态误差,其中Z*=0是唯一的平衡点,Z(tk)表示第k步迭代结果.以e(0)=Z0为初始状态,则状态误差满足e(k+1)=Ge(k),进而有e(k)=Gke(0),上式两边取范数得:
||e(k)||≤||Gk||·||e(0)||=(||Gk||1/k)k·||e(0)||
故||Gk||1/k的大小决定状态误差e(k)收敛到零向量的速度, ||Gk||1/k越小,收敛速度越快.由于:
其中,ρ(G)是矩阵G的谱半径,其值等于矩阵G的所有特征值的复数模最大值.当ρ(G)<1时,迭代格式收敛,ρ(G)越小,收敛速度越快.
3.1 计算方法

以2.2(1)的讨论为例,取m=10,Δt=0.01.令λ=reiω代入(18)式中,得:
pG(λ)=r12e12iω-1.998r11e11iω+0.9980r10e10iω+
(0.4997×10-4kp+0.9990×10-2kd)reiω-
0.9990×10-2kd+0.499×10-4kp
(20)
当ω=0时,即λ=r,由pG(r)=0求得临界曲线中的一条直线l1,再根据隐函数定理,其斜率为:
(21)
当ω∈(0,π)时,由pG(reiω)=0得到参数方程:
kp(ω)=H1(r,ω)
kd(ω)=H2(r,ω)
(22)
上述参数方程表示临界曲线中的另外一支曲线l2.由pG(λ)的连续性知:
故l1与l2在ω=0处相交,并且相切情形发生在ω=0处.不难算出曲线l2在ω→0时的斜率:
(23)
曲线l1与l2发生相切时,即:
S1(r)=S2(r)
(24)
可解得r(0 如图4所示,在 递减的过程中,分别取r=0.99,0.98,0.97,0.946,临界曲线所围的封闭区域越来越小,直至r=0.946时稳定性区域几乎为空集,区域内部的增益值对应的谱半径都比0.946要小,对应于(16)的所有特征根的模均小于0.946. 图4 谱半径与稳定性区域(m=10,Δt=0.01)Fig.4 Plot of spectral radius and stability regions(m=10,Δt=0.01) 将r*=0.9451代入(22)中,并令ω→0,得: (25) 将上述增益代入(16)中,求出特征函数的零点,所有零点均在以r*为半径的圆内,此时ρ(G)=r*. 固定时滞量τ=mΔt=0.1,考察采样周期为Δt=0.02,0.05,0.1 时的最快收敛速度. 由特征函数及(21)~(25)式可以求出各系统参数下的最小谱半径和最优增益.表2给出4种不同采样周期下最优增益及最快收敛速度的关系,从中可以看出,随着m减小,即采样周期增大,最优增益中的速度增益和位移增益均减小,并且最小谱半径也减小.在相同时间段τ=mΔt=0.1,系统趋于稳态的速度由r*m决定,由表2最后一列可知,采样周期越大,实际的最快收敛速度越慢. 表2 采样周期对最优增益及最快收敛速度的影响Table 2 Effect of sampling period on the optimal gain and the fastest convergence rate 时滞量对最快收敛速度有重要影响,以2.2节中的mΔt=0.1,0.11,0.12,0.13为例,根据3.2节的结果,取Δt=0.01,经计算,得到时滞量与谱半径的关系,如表3所示,采样周期固定时,随着时滞量的增加,系统最快收敛速度将减小. 表3 时滞量对最优增益及最快收敛速度的影响Table 3 Effect of time delay on the optimal gain and the fastest convergence rate 采样PD反馈控制作用下倒立摆系统的稳定性受诸多因素的影响,如采样周期、时滞量、反馈增益等.研究表明,一方面,采样周期的减小可使反馈增益平面的稳定性区域会增大、最快收敛速度得到提高.时滞影响了反馈控制的性能:时滞量越大,系统越难以控制,这极大地减小了稳定性区域的大小,同时降低了最快收敛速度.另一方面,如果适当增大采样周期,即降低对采样器性能的要求,虽然会使得稳定性区域减小,最快收敛速度减小,但是,相应的反馈增益可能会大大减小,即降低了对作动器性能的要求.在实际应用中,应根据现实条件与需求来设计控制策略,合理地采用作动器、采样器以及控制指标来设定相关参数.

3.2 采样周期对最快收敛速度的影响

3.3 时滞量对最快收敛速度的影响

4 结论

