高速切削过程中颤振现象的二自由度非光滑模型分析

刘喻 张思进† 殷珊

(1.湖南大学 机械与运载工程学院, 长沙 410082) (2.湖南大学 湖南大学汽车车身先进设计制造国家重点实验室, 长沙 410082)

引言

在机械加工过程中,切削会引起刀具与工件之间强烈的自激振动,这种不可避免的现象通常被称为“颤振”.由于颤振会降低切削质量和切削效率,降低刀具和机床的使用寿命,因此切削加工过程的稳定性研究获得了国内外学者的广泛关注.自20世纪初Tlusty和Tobias等人[1-3]在切削颤振方面作出诸多开创性研究之后,许多学者在机床切削颤振领域做了大量的研究工作[4-7].目前,刀具颤振的单自由度稳定性分析方法已经成熟,两自由度的颤振分析模型也有许多,而本文提出了一种刀尖横向振动与工件扭转振动相耦合的两自由度系统,并给出了一个分段切削力方程,由此,研究系统转变为非光滑动力学系统.

近年来非光滑动力学系统深受广大学者的关注,许多学者[8-12]对其进行了研究.其中分段光滑系统是一类典型的非光滑系统,其包含了丰富的动力学特性,如：Hopf分岔、鞍结分岔、倍周期分岔等等.熊[13]研究了分段光滑的拟哈密顿系统的多个参数的极限环分支问题.高和陈[14]等以双线性分段光滑隔振系统为理论模型,研究了摒除不利于隔振的非线性动力学现象设计方法.梁和韩[15]研究了一类分段光滑系统并给出了广义双同宿分岔的条件.有关分段光滑动力学系统的更多讨论在专著[16,17]中可以找到.

本文试图揭示二自由度非光滑模型在高速切削过程中的颤振运动的动力学特性,如分岔、混沌运动等等.首先通过对系统微分方程的特征方程的分析,讨论非光滑系统的稳定性.当某个参数达到某一临界值时,系统将产生Hopf分岔,从而有稳定的周期运动.最后,以主轴旋转速度为分岔参数,数值模拟了系统响应在旋转速度增加这一过程中的分岔与混沌现象.

1 切削系统的二自由度非光滑模型

考虑刀尖横向振动与工件扭转振动相耦合的系统(图1),其控制方程如下：

(1)

为简化分析,本文假设环向切削力有以下表达式：

(2)

上式Ω0为工件转动角速度；h为切削厚度,当车刀发生横向振动时,切削厚度会发生改变(图2).设车刀等效长度为l,振幅为w,则有：

图1 切削系统示意图Fig.1 Schematic diagram of the tool-workpiece system

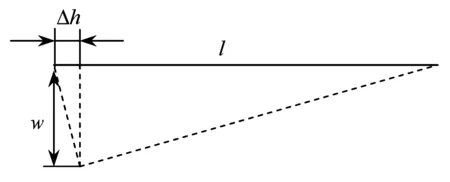
图2 车刀横向振动引起切削厚度改变Fig.2 Change of cutting thickness by the transverse vibration of the cutting tool

(3)

将式(2)和(3)代入方程(1),得到以下向量场分段形式的控制方程：

(4)

和

(5)

引入以下无量纲量：

(6)

对方程组(4)～(5)做无量纲化,得到：

(7)

和

(8)

这里y″、θ″分别是对变量τ的二阶导.τ=ω1t.

此外,作以下变量替换：

(9)

消去方程组(7),(8)中的静态项,有：

(10)

和

(11)

这里

(12)

2 周期颤振运动的非光滑分析

为了便于对系统稳定性分析,方程(10)和(11)可以表示为：

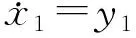
(13)

和

(14)

(15)

(16)

该矩阵特征根方程为：

λ4+aλ3+bλ2+cλ+d=0

(17)

其中：

方程(17)有4个特征根,其中至少有一对共轭复根,对应方程(13)的线性化方程的解为稳定或不稳定焦点(或焦-结点)；而当共轭复根的实部为0时,对应临界情形.为确定该临界条件,令方程(17)的4个根分别为：λ1,λ2,iσ,-iσ.

即方程(17)可表示为：

(λ-λ1)(λ-λ2)(λ-iσ)(λ+iσ)=0

(18)

将(18)式展开,并比较其与(17)式λ同阶项的系数,可得λ1,λ2,σ满足的4个条件,从其中消去λ1,λ2,σ,可以得到方程(13)产生高维Hopf型分岔的条件：

a2d+c2=abc

(19)

若固定方程(17)下方的某特定参数外的其它参数,就可得到该参数的分叉值,如固定Ω外的其他参数即可得到参数Ω对应的分岔值.

由以上分析可知,方程(14)所描述的系统是渐近稳定的,因而其对由方程(13)和(14)组成的分段光滑系统总是耗散的.故分段光滑系统有稳态周期颤振运动的前提是：方程(13)所描述的系统必须是发散的(系统能量增加),如图3所示.

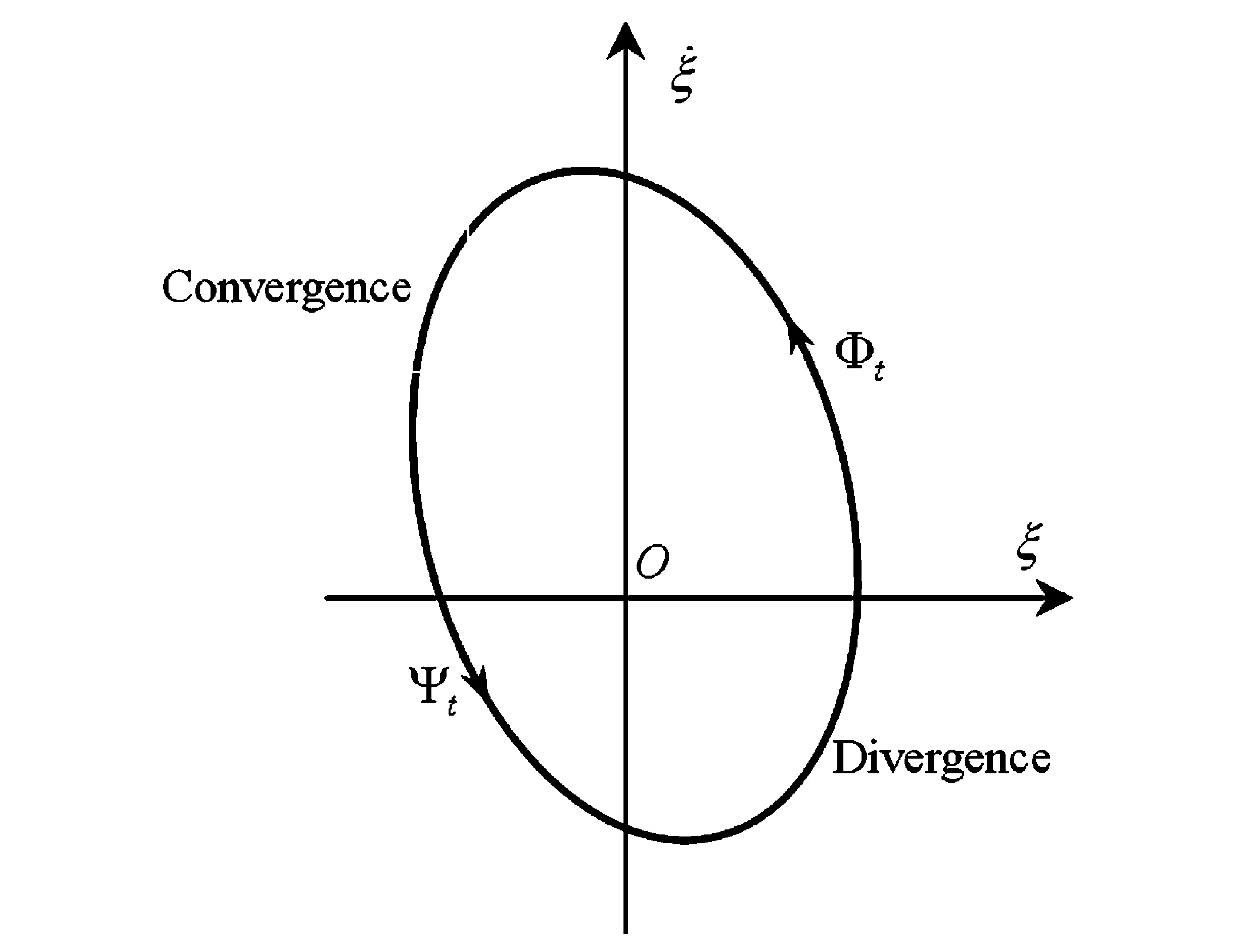
图3 分段光滑系统稳态周期解的产生条件Fig.3 Conditions of stable periodic chatter for piecewise smooth system

因而,式(19)正是分段光滑系统是否存

在稳态周期颤振运动的临界条件.

在条件(19)中带入下列参数值(表1),那么临界条件(19)将变为参数Ω和ω的关系,得到临界线如图4(a)所示.

表1 除参数Ω和ω外的系统参数Table 1 System parameters except parameters Ω and ω

同样带入表2中的参数值将得到参数Ω和μc的关系,临界线如图4(b).

表2 除参数Ω和μc外的系统参数Table 2 System parameters except parameters Ω and μc

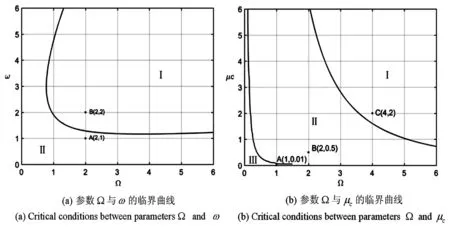
图4 参数Ω分别与ω和μc的临界曲线Fig.4 Critical conditions between parameters Ω and ω, μc

参数Ω和ω的临界线将参数域(Ω,ω)分为两部分：临界线上方区域Ⅰ是稳定的,下方区域Ⅱ是非稳定状态的.为了验证这一结论,在参数域(Ω,ω)中选取了两个点A和B,点A位于临界线下方区域Ⅱ,点B位于临界线上方区域Ⅰ.对于参数B,存在周期一的周期轨道(图5(b)),而对于参数A相应的相空间不存在周期轨道(图5(a)).

图5 在图4(a)中区域Ⅰ和Ⅱ上点对应的相图Fig.5 Phase portrait of points in regionsⅠand Ⅱin figure 4(a)

参数Ω和μc的临界线将参数域(Ω,μc)分为三个部分：中间区域Ⅱ是稳定的,两边区域Ⅰ和Ⅲ是不稳定的.为了验证这一结论,在参数域(Ω,μc)中选取了三个点A、B和C,点B位于中间区域Ⅱ,点A和点C分别位于区域Ⅲ和Ⅰ.对于参数B,存在周期二的周期轨道(图6(a)),而对于参数A和参数C相应的相空间不存在周期轨道(图6(b)和(c)).

图6 在图4(b)中区域Ⅰ、Ⅱ、Ⅲ上点对应的相图和映射图Fig.6 Phase portrait and Poincaré map of points in regionsⅠ、Ⅱ、Ⅲ in figure 4(b)

3 复杂颤振运动的数值模拟

为了便于分析颤振运动的不同类型,带入表3中的数据参数进行数值模拟.并选择无量纲参数主轴速度Ω作为分岔参数,通过模拟系统的分岔图、相图、时域图和映射图来分析参数Ω对系统动力学行为的影响.

表3 除参数Ω外的系统参数Table 3 System parameters except parameter Ω

变量Ω的分岔图如图7所示,从图中可看出,随着分岔参数的增大,系统由周期一运动,倍周期分岔到周期二运动,随着Ω持续增大,再次倍周期分岔到周期四运动.在图7(b)局部放大图中观察更为明显.

图7 参数Ω的分岔图Fig.7 Bifurcation diagram of Ω

图8描述的是在Ω=0.7时的时域图,其中的收敛状态表示稳定的切削状态,并表明在相对较低的主轴速度下切削没有颤振运动产生.随着主轴速度的增大,将会产生hopf分岔.图9显示的是当Ω=2时,系统产生了一个极限环.图9是相平面(x1,y1)的相图.

图8 Ω=0.7处的时域图Fig.8 Time-domain figure when Ω=0.7

图9 Ω=2处的相图Fig.9 Phase portrait when Ω=2

当Ω增大到10时,系统到达了周期二运动状态.随着Ω的不断增大,系统将达到周期四运动,甚至变为周期六运动.

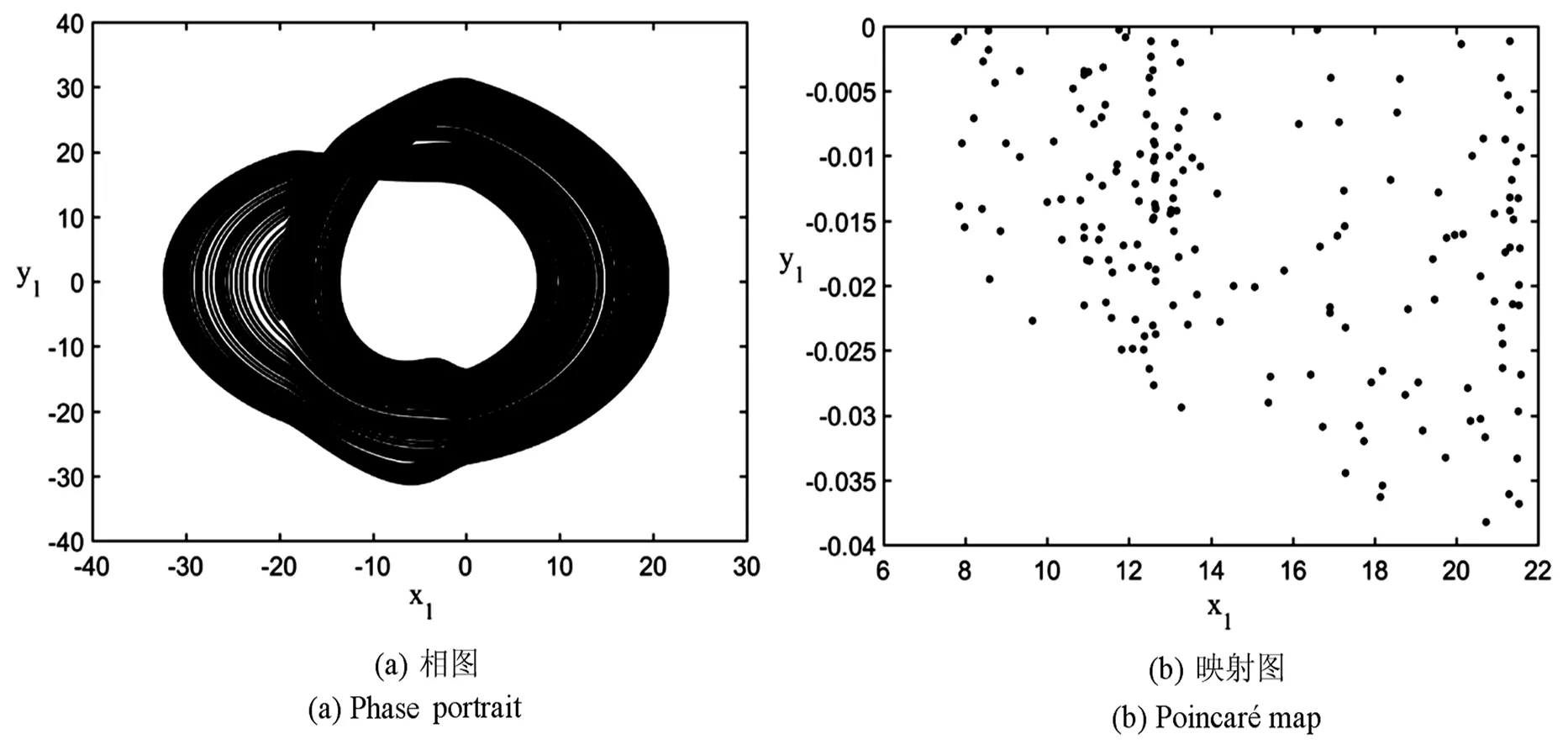
图10 Ω=16处的相图和映射图Fig.10 Phase portrait and Poincaré map when Ω=16

在图10当中的相图和映射图表示系统达到了混沌运动状态,此时,Ω增大到了16.由此可见,切削运动从平衡状态,到周期运动状态,经过倍周期分岔,最后通向了混沌的道路.

4 结论

本文分析了刀尖横向振动与工件扭转振动相耦合的二自由度模型在高速切削过程中的颤振运动,并得到了颤振发生的临界条件,通过数值模拟对临界条件进行了验证,验证结果证明了临界条件的合理性.虽然切削力中的许多参数对削切颤振会产生影响,文中主要研究了最可能的参数主轴速度对系统动力学行为的影响.当主轴速度较小时,系统可能保持稳定的切削状态；当主轴速度超过某个临界值时,系统将可能发生颤振现象.