一种基于正则化和改进GMRES技术的图像复原算法

丁伯伦，凌婷婷，刘树德,2

（1.安徽信息工程学院 基础教学部，安徽 芜湖 241000；2.安徽师范大学 数学学院，安徽 芜湖 241000）

图像在获取、传输、处理的过程中常常会引起图像质量下降问题（受噪声或者成像仪器等影响），这一现象称为图像的退化过程[1]。而图像的复原原理则是一个客观过程，需要利用退化现象的某种先验知识来复原被退化的图像，所以复原是一个针对退化模型，且采用相反的过程进行处理，尽可能复原出原图像的一项技术。

通常情况下，图像退化的一般模型可由下列线性模型来表示：

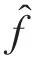
图1 模型流程图

1 基于正则化技术的改进GMRES算法

1.1 正则化技术

正则化方法可看成是一个约束最优化问题，即原始图像f的最优解f′可表示为[2]

这里‖Hf-g‖2为可反映复原后图像对原始图像逼近程度的逼近项；‖Cf‖2为具有约束性作用的正则项；C为正则化算子，常选用二维Laplace算子[3]；μ为具有稳定性作用的正则化参数，一般可根据相应的迭代过程计算出。对模型（2）进行二范数平方项变换[4]即可求出正则化解f′：

通过变型可转化为一个Euler方程：

可以将其看成一个一般形式下的代数方程：

其中A=HTH+μCTC,x=f′,b=HTg。由此就将（2）式利用正则化方法转化为一般的代数方程（3）。

1.2 改进的GMRES算法

基于大型稀疏且非对称的线性方程组：

Ax=b

最有效的求解方法是迭代法[5]，而GMRES算法就是一种迭代方法，并且在计算过程中其具有计算量小、内存占用量低等优势，在求解大型稀疏且为非对称线性方程组的问题时常常被使用[6]。具体方法是先采用Arnoldi正交化过程在krylov子空间上生成一组正交基，再利用QR分解过程解决一个上Hessenberg矩阵的最小二乘计算，来最小化对应残量的计算问题[7]。后来随着GMRES算法的广泛应用，算法也逐渐被改进和优化[8]。而本文提出的是一种改进的GMRES算法，是在最后残量范数计算上改变了‖rk‖的表达形式。

1.2.1 Arnoldi正交化

算法1

Step1：选定元素v1，使得‖v1‖=1；

Step2：对j=1,…,k有vj+1=Avj

对i=1,…,j有hi,j=(vj+1,vi),vj+1=Avj-hi,jvi；

Step3：hi,j=‖vj+ 1‖,vj+1=vj+1/hj+1,j。

1.2.2 改进的GMRES算法

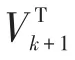
上式仍是一个最小二乘问题，与原GMRES算法相比，这里只是改变了残量范数的最终表达形式，因此可以根据最小二乘法求解出，即得到所需要的近似解，最后根据残量rk的结果决定迭代是否终止[10]。具体过程如下：

算法2

Step1：选定初始值x0，计算残量r0=b-Ax0；

Step2：利用算法1求出一组正交基Vk；

Step4：根据残量rk结果决定迭代是否结束；

Step5：若结果不满足，需令xk=x0,rk=r0，调入Step2重新开始迭代。

这里将改进的GMRES算法与正则化技术结合起来，即可求出方程组（3）的解，得到的结果即为复原出的原始图像。

2 数值实验

实验需要先对原始图像进行退化处理，这里选择依次对原始图像添加尺寸为5*5的均匀模糊，方差为0.001的高斯噪声[13]；相对位移为15像素、模糊方向为45°角的运动模糊加方差为0.01的高斯噪声；同样的运动模糊加噪声密度为0.1的椒盐噪声。针对这些退化图像，将本文的方法、原GMRES算法分别与正则化技术结合来进行复原，并在每一次的退化图像处理中，对比分析这两种方法所复原出的图像，检验最终的复原效果并给出可以甄别图像复原效果的峰值信噪比的比较。

图2是经过5*5的均匀模糊，加方差为0.001的高斯噪声产生的退化图像采用两种方法复原的结果。

图3是经过相对位移为15像素、模糊方向为45°角的运动模糊且添加高斯噪声产生的退化图像采用两种方法复原的结果。

图4是经过相对位移为15像素、模糊方向为45°角的运动模糊并添加噪声密度为0.1的椒盐噪声产生的退化图像采用两种方法复原的结果。

图2 均匀模糊加高斯噪声产生的退化图像复原效果图

图3 运动模糊加高斯噪声产生的退化图像复原效果图

图4 运动模糊加椒盐噪声产生的退化图像复原效果图

实验结果对比可看出，复原后的图像在视觉效果上与画质内容上均有很大提高，而且本文提出的改进GMRES算法要比原标准GMRES算法复原的视觉效果要略好一些。

实验后可以根据峰值信噪比（peak signalto noise ratio，PSNR）来反映算法对退化图像的复原效果，PSNR表示复原后的图像较于退化图像的改善效果[14]。

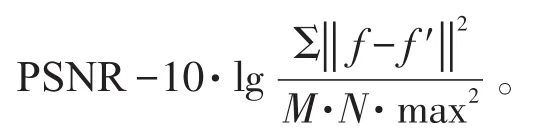
其中max是图像的最大像素值，M表示对应在图像行上的像素数量，N表示对应在图像列上的像素数量，f为原始图像，f′为复原后图像[15]。并将本文方法和原标准GMRES方法复原得到的PSNR值进行对比分析。

当峰值信噪比PSNR值越大，说明复原后图像的失真率越小，复原的效果越好。从表1中的数据可以看出，本文提出的一种改进的GMRES算法的峰值信噪比比原GMRES算法略大，说明在一些原因导致图像退化的情况下，本文的方法在复原效果上要比原GMRES算法更好一些。

表1 本文算法与原GMRES算法复原PSNR值比较

3 小结

GMRES算法结合正则化技术可以较好的复原退化的图像。而本文是将改进的GMRES算法与正则化技术结合起来应用于图像的复原，该方法能够解决一些病态问题，完成复原退化图像的目的。通过数值试验模拟，最后得到的复原图像在视觉效果上和用来评价图像复原性能的峰值信噪比（PSNR）上均说明了方法的有效性，并且比原GMRES算法的复原效果要好。