火箭滑橇的多体系统有限元动力学分析及仿真*

张建华，王 娟，祝 强

(1.长安大学 理学院，西安 710064；2.西安工业大学 机电工程学院，西安 710021)

火箭滑橇是将被试验件放置在滑橇上，以火箭发动机为动力源，对在特制轨道上固定的滑橇体进行高速推进，来模拟被测试件实飞过程中的大过载力学环境的装置.随着运行速度的提高，火箭滑橇面临严酷的气动、振动、烧蚀等多物理场耦合问题.由于设备的特殊性，加上没有现成的理论及方法可以参考，导致国内产品更新换代速度大大落后于美、俄等国.所以从低速起认识火箭滑橇沿轨道贴地面高速滑行的理论，并建立对应的仿真流程十分迫切.

以往火箭滑橇的设计仅凭经验，采用大安全系数来保证滑橇及其上搭载设备的安全性，不仅增加了发射成本(需要更大功率,更多个数的火箭发动机)，还增加了滑橇高速滑行中发生倾覆甚至脱轨的几率.文献[1]利用冲击响应谱分析原理对实测数据进行了动态路谱分析,通过多点测量数据的统计平均处理得到整个路段的不平顺，并且考虑了火箭橇与滑轨的耦合作用，可以作为火箭橇的随机激励条件.文献[2]根据火箭橇垂向冲击模型与轨道不平顺功率谱密度函数,建立了轨道不平顺波长、高差与火箭橇自然频率、速度几者之间的关系式.但是均未给出如何加载及激励模拟的方法.文献[3]从计算流体力学的角度分析了单轨火箭滑橇超音速近地飞行时的气动特性，但是没有考虑轨道及滑靴对系统整体的影响.目前，尚没有将多体系统及有限元相结合的方法应用于火箭滑橇研究的相关文献.

本文在吸收以上研究方法的基础上，建立了多体系统有限元理论，以火箭滑橇为样机原型，用联合仿真的方法验证此理论的可行性；其后处理结果与实物试验所测的数据进行比对，证明了理论及仿真模拟过程的合理性，为更高速度火箭滑橇的设计提供理论和方法上的支持.

1 多体系统的有限单元法

参照弹性力学的相关理论，对连续体做线弹性和小变形的假设，用有限单元法对此连续体分网[4].连续体在t+τ时刻的瞬态动力学方程为

(1)

式(1)还可以简写为：

(2)

式中：Mi、Ci、Ki分别为质量矩阵、阻尼矩阵和刚度矩阵；λi为作用在连续体上的耦合载荷向量.

(3)

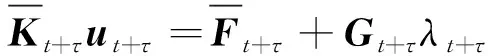
(4)

(5)

对式(5)可以构造如下泛函：

(6)

变换式(5)，可得：

(7)

代入式(6) 可得：

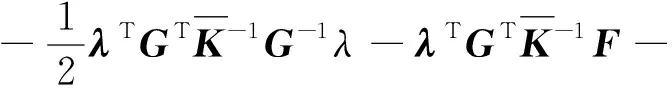
(8)

对式(8)求极值，整理可得：

Kλλ=Fλ

(9)

多体系统有限单元法即对以下的联立方程组进行求解：

(10)

多体系统动力学的研究对象是多柔体和多个刚体所组成的系统，并且各个体之间须有相对运动[5-7].而火箭滑橇各个体之间基本没有大的相对运动，表面看研究对象不适合多体系统理论，但基于两个原因使本研究采用多体系统动力学的方法，一是火箭滑橇各个组成体之间虽没有大的相对运动，但是在某一工况下，仍然会出现微小的相对运动；二是滑靴与导轨之间的相互作用是火箭滑橇的运行安全与否的关键因素，而滑靴与轨道之间有大幅度相对运动存在.

要提高火箭滑橇运行状况的计算机模拟精度，必须考虑一些关键部件(如滑靴)的柔性体特征对整个系统的影响.这在本质上需要多体系统有限元理论来解决此问题，将多体动力学与有限元法无缝衔接，如图1所示.

图1 联合仿真流程

在ANSYS中建立要重点考虑零件的有限元模型，利用专用接口将所需的模态中性文件(.mnf)导入ADAMS中，包含所研究零件的所有柔性数据，刷新ADAMS后可在界面中显示该柔性体零件的模型.添加必要的运动副以便与先前导入的模型连结组成刚柔耦合多体系统模型，然后根据火箭滑橇的具体工况定义相应的外载荷后即可对此试验平台进行动力学仿真.

2 构建火箭滑橇多体系统有限元模型

火箭滑橇的多体模型的建立，需注意其物理及几何简化，物理简化是抽象成物理模型，而几何简化是提高分析成功的几率；在理解各个零件的链接关系的基础上，定义运动连接副，校验总自由度；抽象火箭滑橇在各种复杂工况下所受载荷，对动力学模型进行加载；校核加载后的动力学模型，与实物试验进行比对，调整其精度以符合误差要求；将仿真结果与实物试验所得的结果进行比对，进一步校核模型.

2.1 简化模型

建立火箭滑橇多体动力学模型时做了如下假设和简化：火箭滑橇沿轨道作直线滑行，车身相对于地面水平移动；滑橇结构为左右对称；除要重点考察的零部件外，其余零件均假设是刚体，在整个模拟分析过程不考虑其变形；三维实体建模时，要注意适当的简化模型，删除小倒角及倒圆，去掉小孔及小沟槽等不影响计算精度的小结构，防止加载计算时出现奇异或计算量过大而导致计算失败.

2.2 总体坐标系的建立

在建立刚柔耦合多体模型时，适当坐标系的选择对求解方程的难易程度及多体系统模型的复杂程度至关重要.这里采用了ISO坐标制.以火箭滑橇的图纸参考系为标准笛卡尔坐标(Creo的全局直角坐标系)，坐标原点为后面两个滑靴连线的中点(X轴指向滑橇航向，Y轴指向滑橇横向，Z轴指向滑橇纵向).

2.3 滑橇三维实体模型的建立

用Creo作为火箭滑橇的三维实体建模工具，是由于Creo支持抛物面格式(Parasolid)，而ADAMS正是基于Parasolid格式的仿真软件，在将三维模型导入时不会破坏模型拓扑结构.在ADAMS中建立典型约束、力等力学模型，将实际铰链抽象为初级约束与普通约束，来模拟滑橇各个部分之间的装配和连接.

实体模型分为两部分，即提供动力的火箭引擎车及搭载导引头的试验转台车，主体结构都为某型号角钢焊接成的钢架结构，通过滑靴固定在滑轨上.为防止滑橇脱轨，滑靴做成半包围结构抱住滑轨，滑靴和导轨之间需保留一定的间隙，保证在火箭发动机点火时橇体能顺利启动，间隙亦不能太大，防止滑橇初始运行阶段的跳动；车体与滑靴用某型号销轴连接，滑靴同钢轨以接触摩擦副固定.火箭引擎车上搭载火箭发动机，而试验转台车上搭载三维数控转台来模拟导引头飞行时的姿态(即测试件设备，如图2所示)，两个车体之间通过搭配适当数量的某型号减震器而接触.

图2 火箭滑橇实体模型及多体模型Fig.2 Multibody & entity model of rocket sled

2.4 火箭滑橇的虚拟装配

虽然在Creo中，在设计好各个零件以后，已经对所有零件进行了装配，建立了火箭滑橇的整体三维实体模型(如图2(b)所示)，但是此实体模型并没有添加机械运动学分析中的链接关系，即运动链接副或铰.所以，在ADAMS中必须重新进行装配，即不但要确定各个零件的空间位置，还要用合适的链接副模型去定义它们之间的接触关系.

2.5 火箭引擎车和试验转台车的虚拟样机装配

按照实体建模的先后顺序，在多体系统建模时分别建立提供动力的火箭引擎车及搭载试验设备的试验转台车包含运动链接副的装配模型.为提高计算精度，在不影响分析精度的前提下，只建立主要的链接副.

表1为相关链接副的类型定义，其中Engine_Sled表示火箭引擎车，Turntable_Sled代表试验转台车，Damping _Spring代表两橇车之间的弹簧减振器.

Rocketsled为多体系统模型的名字，软件中的每个零件均有Rocketsled前缀，说明它们的隶属关系.火箭引擎车(Engine_Sled)和试验转台车(Turntable_Sled)通过销轴(Pin)和滑靴(Slider)保持链接，而滑靴与钢轨之间通过滑移摩擦副保持连接，并且只定义一个航向自由度.引擎车和销轴以转动副保持连接，共有四组链接；转台车也有四组转动副同四个滑靴保持链接.这样共有8个滑靴靠它们之间的几何形状约束及滑移接触副与两条钢轨相连.转台车和引擎车靠左右两组接触副连接在一起，引擎车和其上装载的火箭发动机以固定副连接，转台车和其上的三维数控转台底座由固定副连接在一起.T代表三维数控转台(Turntable)，S代表滑靴，将每个橇车上的4个滑靴位置定义为:FL 代表左前位置，BL代表左后位置，FR代表右前位置，BR代表右后位置，限于篇幅，具体的链接副省略.

表1 滑橇多体动力学模型中的运动链接副类型Tab.1 Types of Motion Pair in the Rocket Sled

3 滑橇多体系统有限元模型的边界条件

3.1 火箭滑橇运行过程中风载荷的计算

将火箭滑橇在运行过程中的风压根据伯努利原理等效为风载荷的作用[8]：假如火箭滑橇以300 m·s-1的速度高速飞行，可以等效为火箭滑橇静止，风以300m·s-1的速度作用在滑橇上.

风的强度通常用风压表示，风速和风压的关系表示为

式中：ρ为空气密度(t·m-3)；v为风速(m·s-1).

在标准大气压下，1/2(r/g)约为1/1 630，各地风压情况不同，数值也不同，依据我国风压的相关规范，统一取为1/1 600.所以火箭滑橇在300 m·s-1时的风压为56.25 kN.在实际的动力学仿真和有限元模拟中即可将计算所得的风压作为面力运用到实际计算中.

3.2 轨道定义

试验转台车在火箭引擎车的推动下沿轨道做高速滑行，以通断靶系统测量它们运行到钢轨某一位置的时间.火箭滑橇专用钢轨横截面与一般铁路钢轨一样，但要具有比较高的直线度和平整度，并在每次试验前均要予以校正.尽管如此，不平度仍不可避免，本文以某种实测的铁路轨道表面谱[1-2]来模拟滑橇轨道不平度.轨道表面谱在ADAMS的输入可以采用以下的方法：在轨道表面谱上采集约20个采样点，然后在ADAMS的函数工具箱里(Fuction Builder)用样条曲线进行拟合，用驱动(Motion)来模拟.

3.3 火箭引擎的脉动推力的输入

火箭引擎的推力用样条函数来模拟.在ADAMS中的函数库中选取AKISPL()函数来定义火箭引擎的脉动推力：

AKISPL (Time,.Rocket Sled.Driver_time,

Rocketsled.Spline_i,0)

其中Time为火箭滑橇高速滑行时在轨道上的时间点，由通断靶来提供；.Rocketsled.Driver_time 为火箭引擎的点火时间；.Rocketsled.Spline_i为第i个火箭引擎的出厂推力曲线(这是根据一组实测数据由火箭引擎制造厂家绘制的一条推力曲线，在ADAMS中用Spline函数拟合成一条样条曲线)，由于只有一个火箭引擎参与工作，在此试验中i为1.火箭滑车多刚体动力学模型示意图如图3所示.

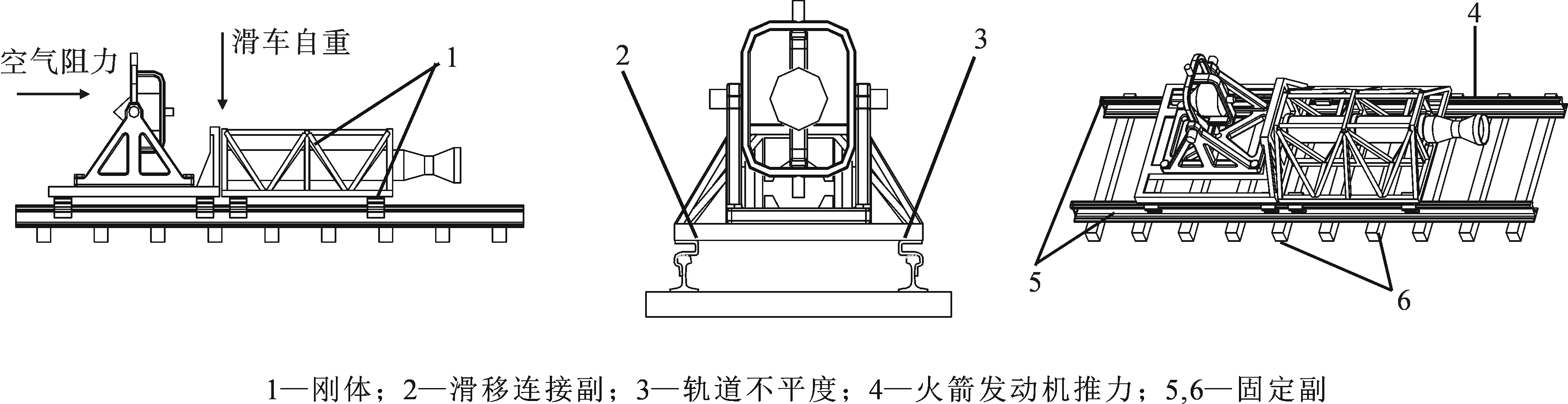
图3 火箭滑车多刚体动力学模型示意图

3.4 施加轨道不平度激励

通过选择火箭滑橇系统和大地的移动副约束，创建直线位移驱动，施加由轨道不平度位移谱图中取的20个位移点值.根据钢轨表面不平度的频率计算时间间隔为0.257 s，把20个位移点作为输入数据，代入特定的函数中，定义位移驱动约束函数.选取20个数据点即前后4个滑靴的轨道模拟数据(前、后滑靴的时间滞后值由于滑橇的运行速度太快而忽略)，分别建立前、后四个滑靴数据输入文件.每个文件有两列数据，第一列是时间，第二列是位移，这样将轨道不平度的模拟数据以函数的形式输入到ADAMS/View中.

本文使用的函数跟火箭滑橇发动机推力模拟函数一样的样条函数，以此样条函数将轨道不平度的模拟数据迭代施加到了滑靴上，再由滑靴传到滑橇体.然后进行多体系统分析处理计算，选择分析结束时间为5 s，步长为50.

3.5 施加火箭发动机推力

火箭引擎车受到固定其上火箭发动机的推力，火箭推力函数由函数库中的AKISPL(Time,.Roc ketsled.Driver_time,.Rocketsled.Spline_n,0) 来模拟，给定时间，滑橇加速前进，经过一段时间之后，运动达到三维数控转台需要的速度280 m·s-1，甚至更高.因在实物试验时轨道涂过润滑油，所以将静摩擦系数定为0.46，动摩擦系数为0.28.

3.6 施加空气阻力

由前文可知，在300 m·s-1时空气阻力为56.25 kN，将其作为sforce施加上火箭滑橇车体、滑靴、鞘轴等merge成的刚体上.

4 仿真结果及分析

4.1 三向过载结果

通过计算得到火箭滑橇三个方向上去噪后的加速度曲线，如图4所示.

从图4可看出，上下方向过载约为16 g、左右过载约为12 g，航向过载约为8 g.而根据某靶场的实飞试验，用加速度计测得滑橇在纵向过载为14 g，横向为10 g，振动频率约5 kHz，振幅不明.可见与实际试验相比较，差距在许可的范围内，说明前述理论、仿真模型及边界条件模拟方法合理.

4.2 柔性体滑靴的有限元分析

由于火箭滑橇与导轨接触的滑靴的强度关系到滑橇高速运行安全性的关键部件，所以需对其受力及疲劳强度做重点跟踪.进入ANSYS程序主界面，通过Creo与ANSYS的专用接口将滑靴实体模型导入到ANSYS软件环境中，在ANSYS中建立滑靴的实体模型，并选择Solid45单元来划分网格.如前文所述，此处需注意在滑靴的转动中心(与销轴的联接处)必须有节点存在，即一定要有外部节点，但是在联接处滑靴为销孔，没有材料，故需在此处创建一硬点，以此硬点作为外部节点.具体的滑靴有限元模型如图5所示.

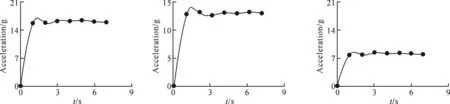
图4 火箭滑车三向过载曲线图

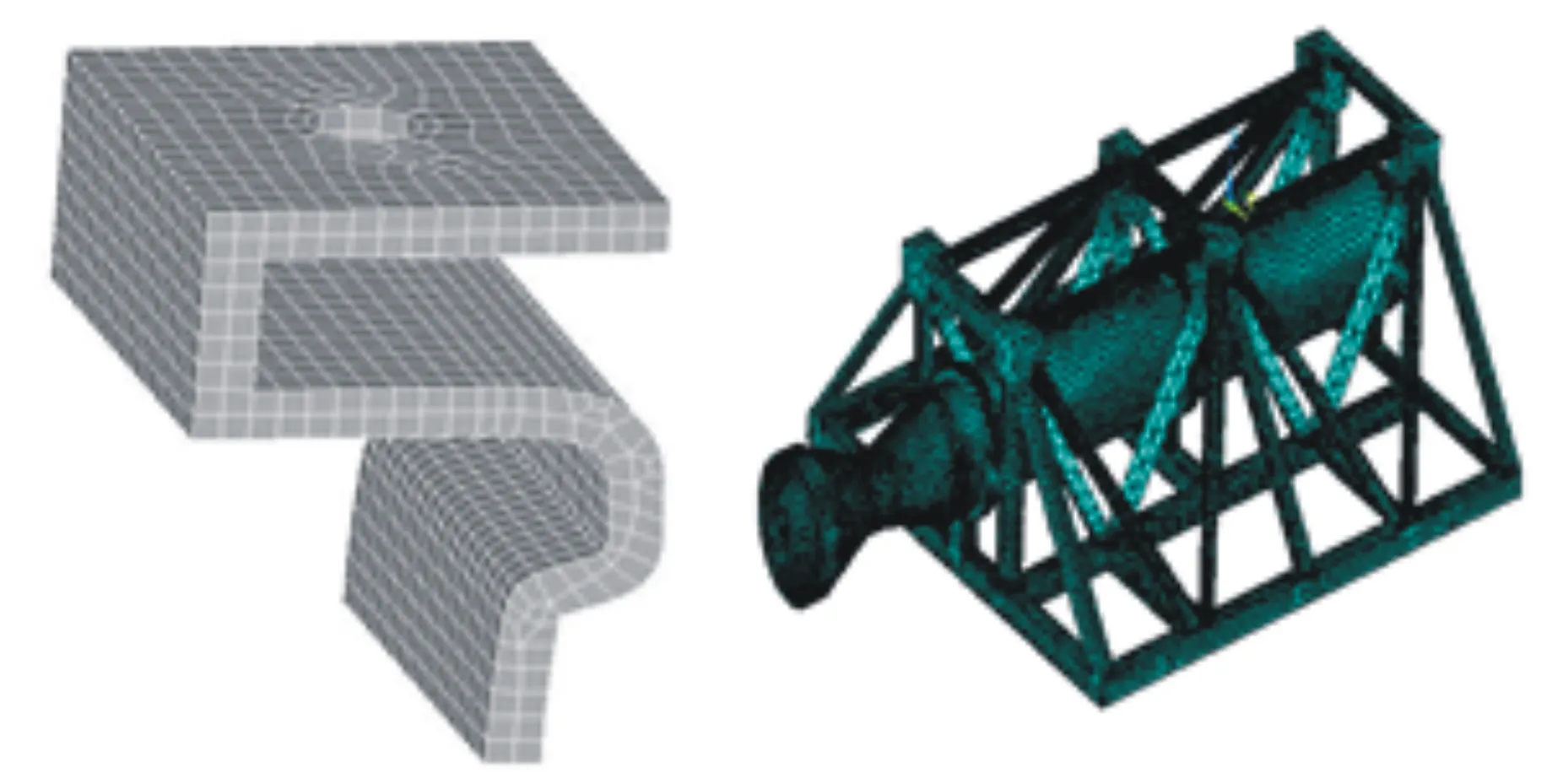
图5滑车体及滑靴的有限元模型
Fig.5 Finite Element Model of Slider and Sled

将滑靴进行模态分析，导出模态中性文件到ADAMS中，进行多体系统动力学分析，输出仿真结果.这里共划分为59 163个单元，20 587个节点.

4.3 输入ADAMS得到的载荷文件

建立滑橇系统的刚性部件，再以引擎车为柔性体，读入滑靴的模态中性文件.mnf以建立柔性体的模型，指定柔性体与刚性体的连结方式，按实际情况定义载荷和边界条件.在分析完成后将载荷文件输入ANSYS.载荷文件包含对应运动过程中不同时刻点柔性体的运动状态和所承受的载荷等数据(例如力，加速度).由于滑靴所受到的载荷通过鞘轴传到滑橇体上，所以可以将载荷间接的加到滑橇体上，分4个时间段，得到滑橇体的变形如图6所示.

图6 滑车引擎车车体变形图

4.4 提高速度重新计算

将滑橇运行速度增加到500 m·s-1以上时，用相同的模拟方法，得到仿真结果.通过后处理发现，三向过载分别达到了纵向30 g，横向25 g，航向15 g左右，可以看出滑橇的三向过载增大显著，运动过程变得更为恶劣.500 m·s-1的速度下，再以另一种轨道功率谱作为边条输入，加大轨道的不平度，重新加载计算，三向过载高达38 g、29 g、17 g.

5 结 论

1) 滑橇的刚度完全满足要求，为保证一定的安全系数，可以适当的加横梁和纵梁以增加滑橇的刚度，滑靴对滑橇的约束作用也可以限制一部分滑橇的变形.

2) 在加大滑橇运行速度到500 m·s-1以上时，滑橇的三向过载显著增大，滑橇及其上三维数控转台的运动变得极为复杂，不能满足搭载导引头进行试验的要求，所以初步得出火箭滑橇载三维数控转台试验方式在500 m·s-1不可行.

3) 在后续的研究中，要考虑滑橇的气动外形，对滑橇跨音速及超音速的情况做流固耦合分析，还应考虑地面效应及滑靴摩擦热的影响.