也谈不等式p或不等式q恒成立问题*
●
(楚水实验学校高中部,江苏 兴化 225700)
不等式p或不等式q恒成立问题一直是高中数学学习的难点.“不等式p或不等式q恒成立”为什么不等价于“不等式p恒成立或不等式q恒成立”;如何求解“不等式p或不等式q恒成立问题”中的参数范围?文献[1-4]中几位教师进行了研究,笔者收获颇多,同时有意犹未尽之感.能否把这个问题论述得更清晰些,同时给出解决这类问题的一般方法?笔者从数形结合角度进行了尝试.
1 引例呈现
例1[1]已知a
2 典型错解
错解已知a
a<(x+1)min或a>(3x-1)max,
从而
a<1或a>5.
3 图形释疑
显然由a
作直线y=a与线段y=x+1(其中x∈[0,2]),y=3x-1(其中x∈[0,2]).
1)当1

图1 图2 图3
2)当2
3)当3
4)当a=1时,显然可得a
5)当a=2,3,5时,显然可得a
因此,引例的解应为a<2或a>5.
4 小结提炼
至此,我们发现:
1)“不等式p或不等式q恒成立”一般不等价于“不等式p恒成立或不等式q恒成立”.
2)由于图像的直观易懂,数形结合应该是首选办法.
3)把刚才的解答过程一般化,可以提炼出解决这类问题的通法:在形如“a为参数,不等式p或不等式q对x∈D恒成立,求实数a的取值范围”的一般题型中,取定某个参数a,从图像上观察得出不等式p的解集E、不等式q的解集F.若D⊆E∪F,则a符合题意;若DE∪F,则a不符合题意.
5 实战检验
由于引例的问题背景为直线,因此直线型不再举例赘述.为了体现方法的有效性,以下就曲线型、离散型作检验.

解原式整理得




图4



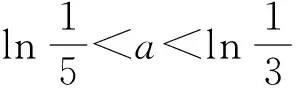


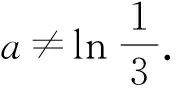
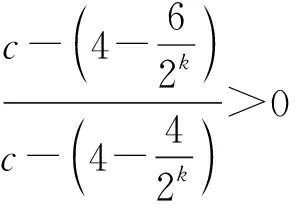
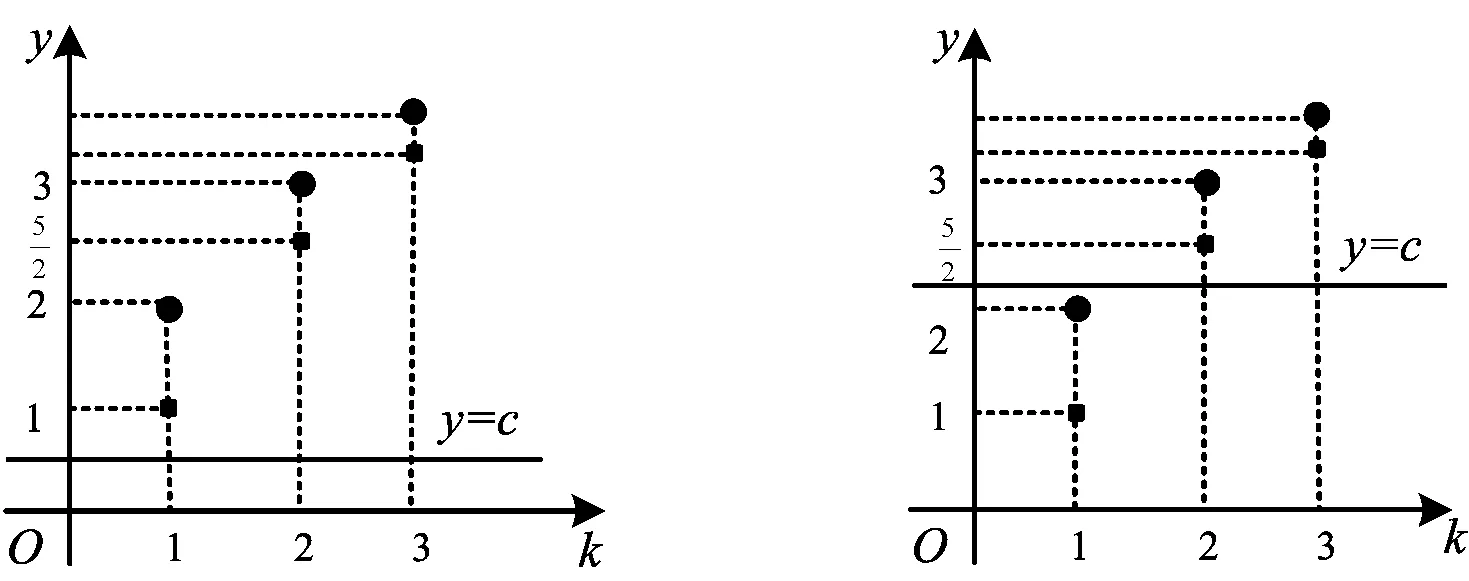
图5 图6




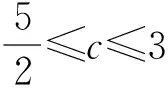

6 一点说明
文中几个例题均通过分离变量转化为简单的函数图像与直线的位置关系进行处理.笔者查阅了相关资料,刊载的“不等式p或不等式q恒成立问题”都可以这样处理.对于不能分离变量的该类问题,公开刊物上目前还没有出现.笔者自编了几个这样的例题,发现要么很简单,要么太难,但处理策略均可归结为通法,即从图像上得出E,F,然后判断D与E∪F的关系.限于篇幅,不作一一演练.

