看似寻常最奇崛 成如容易却艰辛*
——以一道高考模拟题的解题为例
●
(宿城第一中学,安徽 宿州 234000)
宋代王安石在《题张司业诗》中用“看似寻常最奇崛,成如容易却艰辛”来形容张籍作诗看起来很容易,但实际上都是经过艰苦构思才完成的.数学的解题也是如此,一种看似简单的解答,其“背后”可能是解题人的困心衡虑.罗增儒教授在《数学解题学引论》中说:“人们寻找习题解答的活动叫做解题过程,它通常包括从拿到题目到完全解出的所有环节或每一个步骤.每一道习题都有自己的解题过程,每一个过程都可以分成一些循序渐进的阶段.解题过程是运用数学知识、调动数学能力、不断提出问题又不断解决问题的思维过程.”数学的解题是一个充满挑战、蕴含无限魅力的思维过程.笔者以一道导数高考模拟题为例谈谈解题的历程及对高三解题教学的感悟,不当之处,请批评指正.
1 题目再现,解法探究
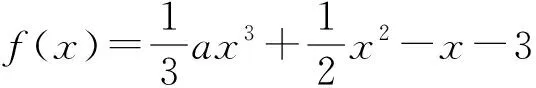
1)当y=f(x)与y=-3相切于点A(x0,f(x0)),求a,x0的值;
2)设F(x)=f′(x)·ex,如果F(x)>-1在(0,+∞)上恒成立,求a的范围.
说明本题是湖南、江西省2018届高三3月份十四校数学联考文科试题的导数压轴题.该试题的命制严格遵循了《2018年普通高等学校招生全国统一考试大纲》和《2018年普通高等学校招生全国统一考试大纲的说明》(以下分别简称为《考试大纲》和《考试说明》)的要求,在考查基础知识的基础上注重对数学思想方法和数学能力的考查,以能力立意,以导数知识为载体,从问题出发,考查思维品质的深度与广度.第1)小题主要考查导数与切线的相关知识,根据切点和斜率列出方程组,解出a,x0的值;第2)小题以恒成立问题出发,考查学生对导数概念的灵活运用,考查利用导数讨论函数的极值(最值)问题,考查学生运算求解能力、逻辑推理能力以及转化与化归的思想.笔者选用了这道题作为学生的练习题,通过对学生作业的批改、统计分析,师生的思维(思想)得到了碰撞(交流),各种解题思路不断涌现.笔者通过和部分学生的交流(对话),各种解法也日臻完善,最终本题出现了精彩纷呈的一题多解.下面仅对第2)小题进行分析.
1.1 试题讲解
解法1(参考答案)因为f′(x)=ax2+x-1,所以
F(x)=(ax2+x-1)ex,
从而
F′(x)=[ax2+(2a+1)x]ex,
且
F(0)=-1.
①当a=0时,F′(x)=xex,可知F(x)在(0,+∞)上单调递增,此时F(x)>-1成立.


不符合条件.


可知F(x)在(0,+∞)上单调递减,此时F(x)<-1,不符合条件.
⑤当a>0时,
可知F(x)在(0,+∞)上单调递增,此时F(x)>-1成立.
综上所述:a≥0.

1.2 学生解答
解法1是不是自然解法?是不是学生想要的解法?学生在作业中给出了回答:不是,近一半的学生首先想到的是分离参数.
解法2(分离参数)因为F(x)=f′(x)·ex>-1,所以
(ax2+x-1)ex>-1,

再记h(x)=(x+2)e-x+x-2,则
又记φ(x)=ex-(x+1),则
φ′(x)=ex-1>0,
从而φ(x)在(0,+∞)上单调递增,即
φ(x)>φ(0)=0,h′(x)>0,
于是h(x)在(0,+∞)上单调递增,即
h(x)>h(0)=0,g′(x)>0,
进而g(x)在(0,+∞)上单调递增.根据洛必达法则
故a≥0.
点评什么是自然解法?不同的人会给出不同的回答,但是笔者认为只有解题人自然(首先)想到的才是最自然的.解法2在最后的处理中用到了洛必达法则,属于超前知识,高考解主观题时能不用则尽量不用,但总体来说该解法瑕不掩瑜.
1.3 类比升华
类比含lnx的函数处理方法,考虑分离ex.因为F(x)=f′(x)·ex>-1,所以
ax2+x-1>-e-x.
设g(x)=ax2+x-1+e-x,从而
g′(x)=2ax+1-e-x,
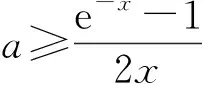

g(x)>g(0)=0,
故ax2+x-1>-e-x成立.
②当a<0时,设h(x)=2ax+1-e-x,则
h′(x)=2a+e-x.

h′(x)=2a+e-x<0,
于是h(x)在(0,+∞)上单调递减,又h(0)=0,进而h(x)<0,即g′(x)<0,故g(x) 综上所述:a≥0. 解法4因为F(x)=f′(x)·ex>-1,所以 ax2+x-1>-e-x. 设g(x)=ax2+x-1+e-x,求导得 g′(x)=2ax+1-e-x. 综上所述:a≥0. 解法5因为F(x)=f′(x)·ex>-1,所以 ax2+x-1>-e-x. 设g(x)=ax2+x-1,h(x)=-e-x,则 h′(x)=e-x. 由h′(0)=1,可得h(x)在x=0处的切线方程为 y=x-1. ①当a=0时,不难证得x-1≥-e-x(如图1). ②当a>0时,ax2+x-1≥x-1,从而ax2+x-1≥-e-x成立,当且仅当x=0时取到等号(如图1). ③当a<0时,x→+∞时,g(x)→-∞,h(x)→0(如图2),此时必存在x1>0,当x∈(x1,+∞)时,ax2+x-1<-e-x,不满足条件. 综上所述:a≥0. 点评对于函数g(x)=ax2+x-1,当a>0时,其图像为开口向上的抛物线,与y=x-1相切于点(0,-1);当a=0时,g(x)退化为一次函数y=x-1;当a<0时,其图像为开口向下的抛物线,且与y=x-1相切于点(0,-1).图1和图2直观地呈现了两个函数图像的位置关系,学生容易想象随着a从大到小的变化g(x)图像的动态变化过程.由此揭示了问题的本质,笔者相信这也是试题命制者的初衷. 含参数的导数恒成立问题是高考重点考查的内容之一,一直倍受命题专家的青睐.此类问题的解题切入点很多,体现了灵活运用转化与化归、分类讨论、数形结合、函数与方程等思想方法解题的能力.解决此类问题时,通常有以下4种思路:1)分离参数,转化成一个确定(不含参数)的函数求最值问题,但有时需用到洛必达法则,如解法2;2)直接带参求导,如解法1,该解法需要对参数进行分类讨论,对学生分析问题的能力要求较高,解题时学生容易出现参数分类不完整、分类标准不明确的情况;3)变形后带参求导,对函数进行适当的等价转化,变形后再求导,如解法3,此类问题有着固定的“套路”,如含lnx的函数解题时常分离lnx;4)数形结合,把恒成立问题转化成两个基本初等函数(或容易画出图像的函数)的图像问题,借助图像的几何直观性来阐明函数之间的关系,如解法5. 通过本题的求解历程,笔者对高三复习时的选题、解题及讲题有了些许感悟.高三复习课是高中数学的重要课型,而解题教学是复习课的常见形式,“能否上好解题教学课,让学生从题海战术中走出来,提高学习效率”是高三一线教师必须要深入研究的问题. 高三学生的时间短暂而宝贵,因此高三复习更应惜时如金.若教师不加甄别地随便把一道题目(一张试卷)交给学生去做,学生可能不断重复做着自己会的题目,与此同时不会做的仍然不会做.长此以往,学生便不再思考,只会对数学失去兴趣,亦或是在高三复习时早早地就放弃某些题型(如导数压轴题).波利亚说过:“一个专心的认真备课的老师能够拿出一个有意义的但又不太复杂的题目,去帮助学生挖掘问题的各个方面,使得通过这道题,就像通过一道门户,把学生引入一个完整的理论领域.”因此,教师在选题时要注重精炼且有针对性,同时题目的选择要具有启发性(引导性),能够引导学生去思考,这样才能提高学生的学习效率,提高解题的能力. 解题就像一场思维的旅行,在乎的不是目的地(结果),而是沿途的风景(解题过程)及看风景的心情(思维).但现在有很多师生太注重结果,只要结果对就不考虑解题过程,或者只要结果不对就全盘否定解题过程,这都是以偏概全的.波利亚说过:“中学数学教学首要的任务就是加强解题训练,解题的价值不是答案本身,而是在于弄清怎样想到这个解法的,是什么促使你这样想、这样做的,掌握数学就是意味着善于解题.”在高三,师生在解题时更应做个“明白人”,更应注重解题过程.从解题源头开始,多关心“怎么想到的,又怎样去解的”,按照“怎样解题表”去分析问题、解决问题.只有注重解题的过程,才能养成良好的思维习惯和品质,才能从纷繁芜杂的高三题海中找到解题共性和规律,从而跳出题海. 2014年《教育部关于全面深化课程改革,落实立德树人根本任务的意见》颁布后,中国学生发展核心素养的培养成为数学教育的一项基本任务.高三解题教学不仅要重视落实《普通高中数学课程标准(2017年版)》和《考试大纲》的要求,把握方向,做到有的放矢,还要重视核心素养的培养,通过讲题落实文化基础、自主发展、社会参与等核心素养的要求.如在讲题时多归纳总结,促使学生勤于反思;多审视(重视)学生的错误解法,树立学生的自信心,形成良好的心理品质及抗挫折能力;解题时传统解题教学与信息技术融合,促使学生适应信息化发展趋势.在解题教学中落实核心素养的培养,有利于提升学生的综合素质,促使学生内外兼修、全面发展.


1.4 借助放缩
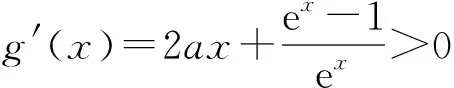


1.5 追本溯源
2 解题感悟
2.1 选题重精炼,注重引导学生思考
2.2 解题重过程,注重学生思维养成
2.3 讲题重落实,注重核心素养提升

