用特解组合法构造两端铰支梁的格林函数

王其申，章礼华，何海敏

（安庆师范大学物理与电气工程学院，安徽安庆246133）

格林函数和格林函数法是数学物理方法教学中的一个重要内容，它们不仅在物理学，而且在工程科学中都有着广泛应用[1-5]。因此，在数学上如何构造所需格林函数，就是一个必须解决的问题。针对不同的定解问题，有多种构造格林函数的方法，其中之一，就是本文将要讨论的特解组合法。历史上，文献中出现了使用特解组合法构造工程构件变截面的杆和固定-自由梁的格林函数的记载[6]。然而，对于同为工程上的重要构件之一的两端铰支梁，能否使用特解组合法构造出它的格林函数，一直没有见诸文献。笔者多次试图完成这项工作，几次无疾而终。在认真总结以往失败的原因之后，本文采用特解组合法，成功构造了变截面的两端铰支梁的格林函数。这一结果表明，在各种构造格林函数的方法中，特解组合法是一种比较简单而又普遍行之有效的方法。

1 特解组合法

特解组合法是一种构造格林函数的方法，现以构造两端弹性支承杆的格林函数为例加以说明。

两端弹性支承杆的平衡方程及其边界条件是

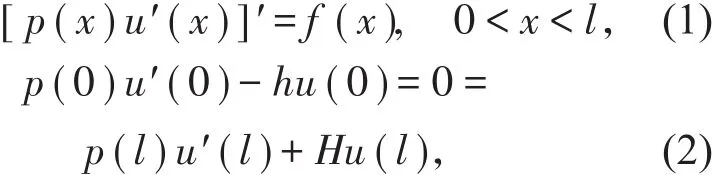
式中，p(x)=EA(x)，E为材料的杨氏模量，A(x)为杆件的横截面积，p(x)＞0是[0,l]上的连续或分段连续函数，它和f(x)都是已知函数，而u(x)是待求区间[0,l]上的位移函数，h和H是杆件与左右两端基础相连的线弹簧常数，它们均为非负常数，此处满足h+H＞0。相应的格林函数G(x,s)的定义则是

式中撇号表示相应函数对变量x求微商（以下均如此表示）。δ(x-s)表示位于x=s处的单位点源密度的δ函数。以上两式的数学含义是：

(1)除x=s外，Green函数满足齐次方程:[p(x)G′(x,s)]′=0，

(2)在x=s处，Green函数的微商满足：

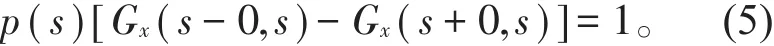
(3)在端点处，Green函数必须满足两端弹性支承杆原有的边条件(2)。

为了构造满足方程(3)和(4)的格林函数G(x,s)，我们先分别求解下列两个定解问题：

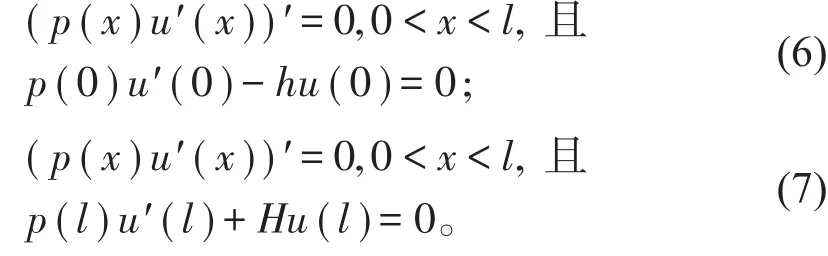
设问题(6)的非平凡解是ϕ(x)，问题(7)的非平凡解是ψ(x)，则两端弹性支承杆的Green函数可以表示为

其中，x,s∈[0,l]。这样确定的G(x,s)显然满足G(x,s)的数学含义中的条件(1)和(3)；通过适当选取常系数k，即可满足条件(2)，即(5)式。

这就是本文所称的特解组合法。

2 两端铰支梁的格林函数的构造

对于变截面的两端铰支梁，它的平衡方程和边条件是

其中，r(x)=EJ(x)是[0,l]上的连续或分段连续函数，且r(x)＞0，它和f(x)都是已知函数，E为材料的杨氏模量，J(x)为梁的横截面对其中性轴的二次矩，而u(x)是待求的区间[0,l]上的位移函数。

相应的格林函数G(x,s)的定义则是

以上两式的数学含义是：

(1)除x=s外，Green函数满足齐次方程:

(2)在x=s处，Green函数的三阶微商（力学上称为剪力）应满足：

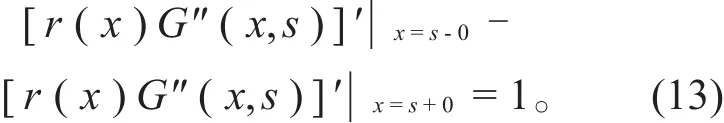
(3)在端点处，Green函数必须满足两端铰支梁原有的边条件(10)式。

由于这里的微分算子是4阶算子，按照上节介绍的特解组合法，设ϕ(x)，ψ(x)是下列问题

的两个线性无关解。χ(x)，η(x)是下列问题

的两个线性无关解。把(14)式中的方程积分两次，得到

式中，C1和C2为积分常数。由(14)式中的第二个边条件，可以得出C2=0。方程两边同除以r(x)后，再积分两次，得到

利用(14)式中的第一个边条件，可以定出C4=0。把上式右端的第一项分部积分一次，最终得到

因此，可取

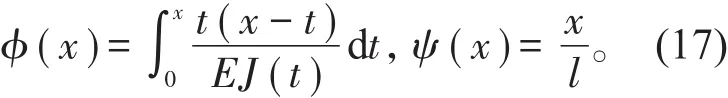
同理，把(15)式中的方程积分两次后，先应用(15)式中的第二个边条件，再把方程两边同除以r(x)后，继续积分两次，得到

最后，利用(15)式中的第一个边条件，有

由此，解得

代入(18)式得

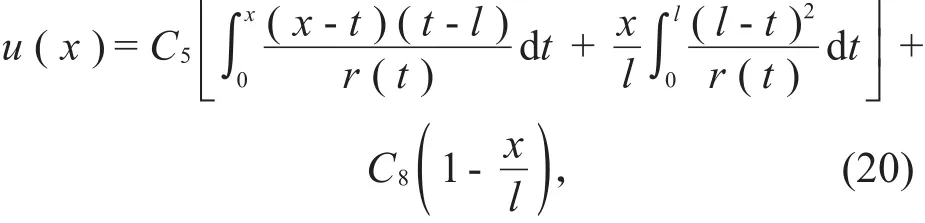
于是，可取

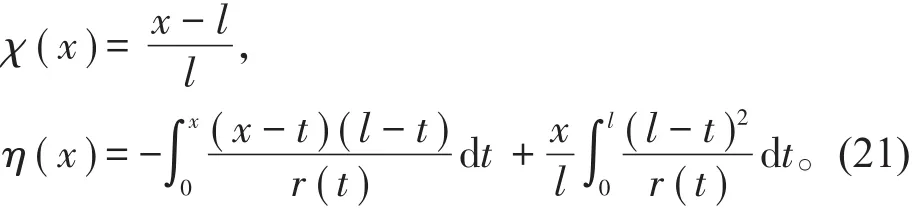
这样，两端铰支梁的Green函数可以表示为

其中，x,s∈(0,l)。这与其他文献的结果完全一致。

3 讨论

从以上求解过程来看，特解组合法是简单的，但在如何选取梁方程在左右端边条件下的线性无关解，亦即如何确定ϕ(x)，ψ(x)和χ (x)，η(x)是需要经验和细心的。

首先，按照(16)式，应取ψ(x)=x，然而在(17)式中，选取ψ(x)=x/l，虽然这没有什么矛盾，但选后者的理由何在？这是因为在(21)式中，我们选取了χ(x)=(x-l)/l，二者量纲必须保持一致。当然，也可以这样选择：

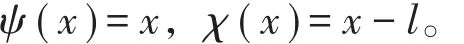
但检验发现，这样选择的结果，(13)式不被满足。于是，为了满足(13)式，格林函数的通式应该改写成

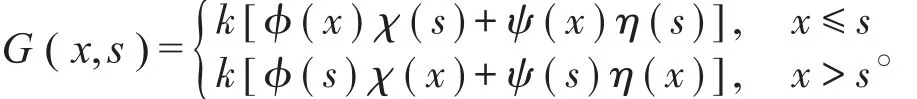
通式中包含一个常数是不难理解的，这样一来，就可以根据(13)式，导出k=1/l，从而获得同样的结果。

其次，以往未能成功构造两端铰支梁的格林函数的主要原因，在于对(19)式的处理。由(19)式，一种很自然的处理方法是

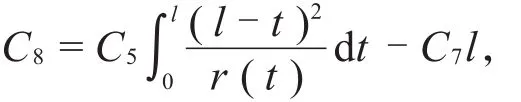
于是(20)式变成

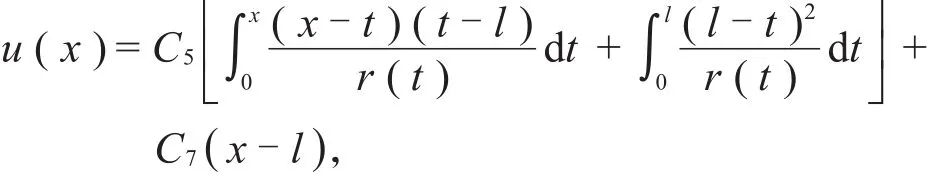
相应的，

就解题过程而言，这样处理毫无错误。这时，注意到η(x)的表达式中第二个积分项的差别，即使选取ψ(x)=x/l，χ (x)=(x-l)/l，仍然不能获得正确的答案。可见，经验和细心在应用特解组合法时多么重要！