空间目标多星多角度实时近距离三维详查研究
许丹丹,张庆展,张 进,罗亚中
(1.国防科技大学 空天科学学院,长沙 410073; 2.上海宇航系统工程研究所,上海 201109)
0 引言
随着航天技术的发展,各航天大国对大中型空间目标在轨补给、维护维修,以及空间失效目标抓捕俘获、拖曳移除等在轨近距离操作方面正开展研究。如:日本早在1997年就实施了ETS-VII计划,开展了自主交会对接、目标星监测、燃料补给等试验[1];俄罗斯于2014年、2015年通过发射宇宙2499卫星、宇宙2504卫星、Olymp高轨卫星对抵近侦查、近距拍照、伴飞监视等空间自主机动技术进行了验证;美国通过实施轨道快车、试验卫星等项目验证了多项在轨近距离操作技术[2-3]。
利用星载传感器获取空间目标的详细信息是成功实现在轨近距离操作的前提。目前,美国已初步具备了体系化的空间目标监测能力,如:MiTEx卫星可协同进行轨道机动及对在轨目标成像监测,以掌握高轨空间态势[4];GSSAP卫星采取双星组网,通过变轨机动对地球同步轨道的空间目标持续开展近距离成像侦察,为美国开展太空活动提供更详细的信息[5]。空间目标监测是掌握和评估空间活动态势的重要保障,对空间目标进行三维观测,获取在轨操作所需信息,并在操作过程中实时监视与评估操作效果,具有重要意义。
ETS-VII计划、轨道快车、试验卫星、MiTEx卫星、GSSAP卫星等项目[1-5]主要集中在单颗卫星的近距离操作方面,而卫星近距离观测研究主要集中在绕飞轨道设计、图像解算等方面,国内外鲜有这方面的研究报道。
单颗观测卫星由于受传感器视场和相对轨道构型等限制,难以快速、准确地完成对空间目标的详查任务,而多星协同工作可携带多种测量设备对目标进行三维观测,获取目标多种频谱特性,具有快速灵活、可靠性高等优点,可弥补观测时空间隙,克服单星对于分散空间目标可能无法连续观测的缺点。
本文针对多颗观测卫星协同近距离绕飞详查任务,综合卫星编队相对轨道运动与观测任务的特点,采用网格统计法分析单/多颗观测卫星对空间目标观测过程中的详查覆盖率、详查最短时间等性能指标,比较不同绕飞距离对观测效果的影响;以绕飞椭圆半长轴、观测卫星相对轨道倾角、相对相位差等为整体设计变量,将观测卫星视场范围、安全性等为约束条件,综合考虑任务要求、任务时间等目标,设计了多颗观测卫星协同工作的策略,并比较了不同编队对任务特性的影响,以实现实时、全覆盖观测。
1 空间观测约束条件
1.1 目标几何模型
简化后的空间目标由1个长方体本体及2个平面板太阳翼近似表征,如图1所示。空间目标本体的坐标系定义为:长方体的几何中心点为坐标原点O,沿着长方体的长、宽、高的方向分别为x、y、z轴,长度方向的单位矢量为dl,宽度方向的单位矢量为dw,高度方向的单位矢量dh=dl×dw。在本体坐标系下可描述长方体、平面板的大小与姿态,确定空间目标的状态。

图1 目标几何模型Fig.1 Target geometric model
假设目标的长方体本体对地定向,则在相对轨道坐标系下,长方体保持静止状态;平面板与z轴方向的夹角为γ,以角速度ω0绕y轴旋转,且ω0与太阳在相对坐标系下的平均轨道角速度相同,γ=γ0+ω0t。旋转平面板的位置坐标类似旋转长方体,任意点P的位置坐标在以原点O为中心的旋转坐标系下可表示为
[x′y′z′]T=TR·[xyz]T
(1)
点P的坐标与自旋轴OM的位置、转动角速度ω有关,自旋轴OM在轨道坐标系下的方向余弦分别为c1、c2、c3,则点P绕OM轴转动λ到达点P′的变换矩阵[6-7]为
(2)
式中:λ=ω(t-t0)。t0时刻,卫星的本体坐标系与相对轨道坐标系重合。
1.2 三维观测约束条件
三维观测采用自然绕飞式编队构型方案,观测卫星对空间目标进行光学观测需满足以下要求。
1.2.1 阳照区
空间目标只有在阳照区才能被观测卫星的可见光传感器所观测,该要求可表示为[8]
(3)

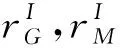
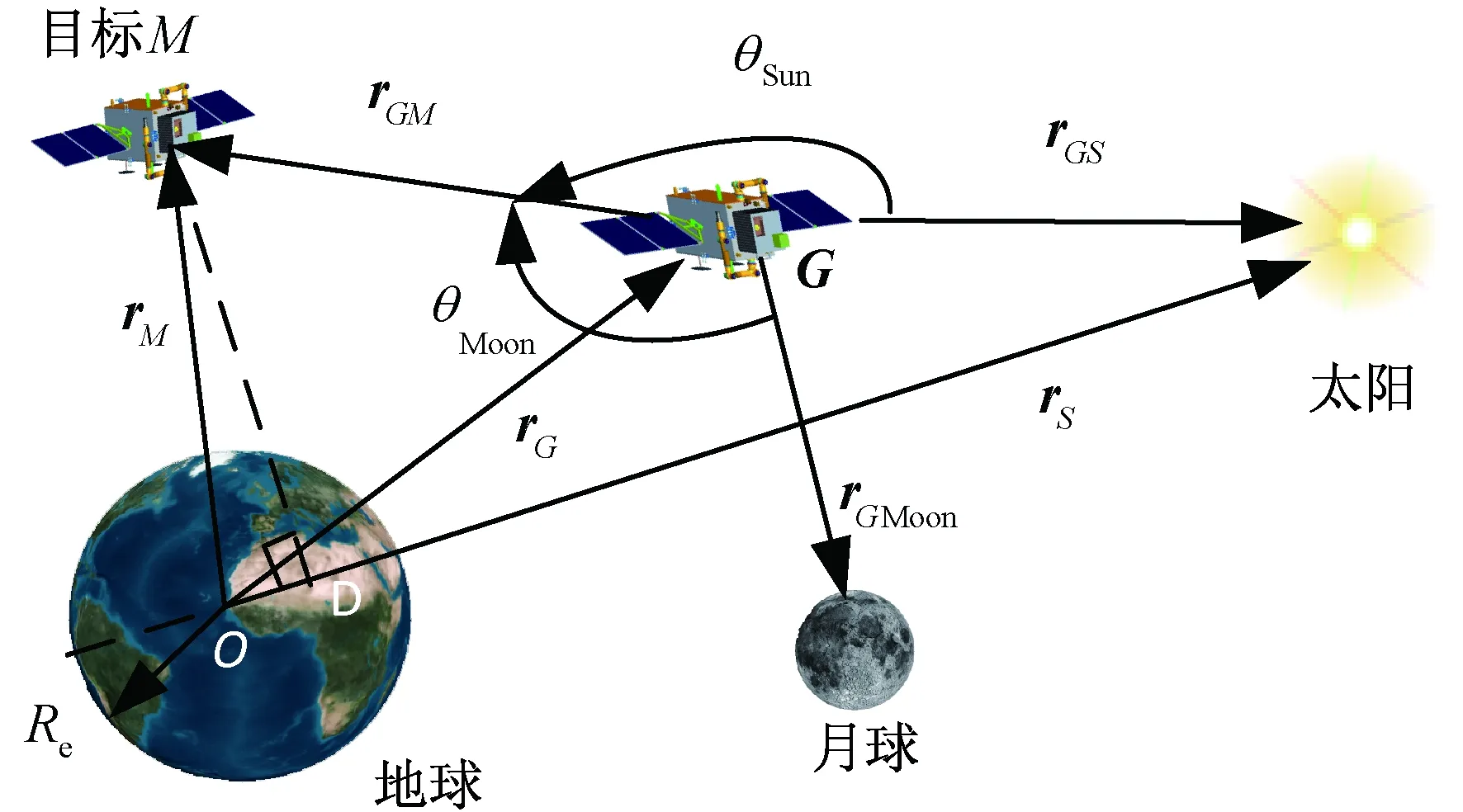
图2 光学可见性约束Fig.2 Optical visibility constraints
1.2.2 视场无强光干扰
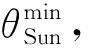
(4)
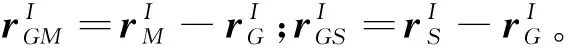

(5)
1.2.3 相对角速度
空间目标与观测卫星的相对角速度为
(6)
1.2.4 观测视场角
观测点与目标的空间几何关系如图3所示。每颗观测卫星均安装视场半锥角为Δg的星载敏感器,敏感器视场中心始终指向目标几何中心。图中:dir0为观测点指向空间目标中心的方向向量;dir1为某成像点指向观测点的方向向量;dir2为空间目标某表面几何中心指向该观测点的方向向量。假设成像点视线方向相对敏感器视场中心方向的夹角为θ、平面正法向量n与观测点方向dir2的夹角为α,则
θ=arccos(-dir1·dir0),α=arccos(n·dir2)
(7)

图3 观测点与空间目标的空间几何关系Fig.3 Space geometric relationship between observation point and target satellite
对长方体表面成像点的可观测性进行分析,判断长方体的某表面是否在观测卫星可观测范围内。若0≤α<π/2,则表示此表面可观测,继续判断表面内部成像点能否被观测:若θ<Δg,则表示成像点在视场内部且未被目标自身遮挡,可观测;若θ≥Δg,则表示成像点不可观测。
2 近距离三维详查任务设计
观测卫星在某一时刻只能观测空间目标表面的一块区域。观测卫星对空间目标进行绕飞相对运动,其相对位置速度不断变化,已观测的区域逐渐增大并连成一片。如果单颗观测卫星绕飞1圈,则只能观测一部分区域,因此,设计不同的绕飞轨道与卫星数量,可以提高观测覆盖率,减少全覆盖详查的最短时间。
2.1 多星绕飞任务相对运动
采用VVLH(当地轨道坐标系)描述观测卫星相对空间目标的运动,其定义为:坐标原点在观测目标几何中心;z′轴指向地心;x′轴沿观测卫星轨道速度方向,处于轨道面内,与z′轴垂直;y′轴由右手法则确定。从运动学角度建立相对运动方程,一阶近似简化后,以轨道根数为参数,将绕飞相对运动描述为
(8)
式中:a,e,λ,Ω,ωc分别为半长轴、偏心率、轨道倾角、升交点赤经、近地点幅角;ωn为轨道平均角速度。
将式(8)简化,相对空间目标的椭圆绕飞轨道运动可表示为[8]
(9)
式中:A为绕飞半径;φ为观测卫星在绕飞轨道上的位置;k为1个无量纲的正数,表示y轴方向上的振动幅值;φ为y轴方向上的振动相位。A,φ,k,φ与运动学参数a,e,ΔΩ,Δλ,ωc的关系为[9]

(10)
采用式(9)表示绕飞相对运动,分离了描述观测卫星在绕飞轨道上具体位置的参数φ,并且描述绕飞轨道的其他3个参数意义明确,便于设计不同的多星绕飞轨道构型。
随着参数A、k、φ、φ的变化,绕飞轨道的形状和空间指向都发生了变化。观测卫星的位置变化对观测目标的覆盖特性有一定的影响。如果配置多颗观测卫星,使它们有不同的A、k、φ、φ,构成不同的绕飞编队队形,则覆盖特性也不同。如果同绕飞轨道的2颗观测卫星对非旋转目标进行观测,观测区域相同,则最大覆盖率没有变化,但达到最大覆盖所需观测时间会缩短。不同轨道观测卫星的轨迹不同,观测条带不同,由多颗卫星对空间目标观测,可提高覆盖率,缩短观测时间,提高任务成功率。
2.2 近距离三维详查的任务设计
2.2.1 单星观测
单星观测分为两种情况:一是假设观测卫星的观测光轴(视线中心方向)始终指向空间目标主体中心;二是假设观测光轴随时间转移,光轴在1个周期内沿y轴方向从空间目标左帆板的最左端匀速转到右帆板的最右端。
2.2.2 3星3轨道观测
设计位于3个轨道面的3颗观测卫星对空间目标进行分区域观测,3个轨道面的倾角间隔为60°,如图4所示。图中:观测卫星a光轴对准空间目标左帆板的几何中心,观测卫星b光轴对准空间目标的几何中心,观测卫星c光轴对准空间目标右帆板的几何中心。
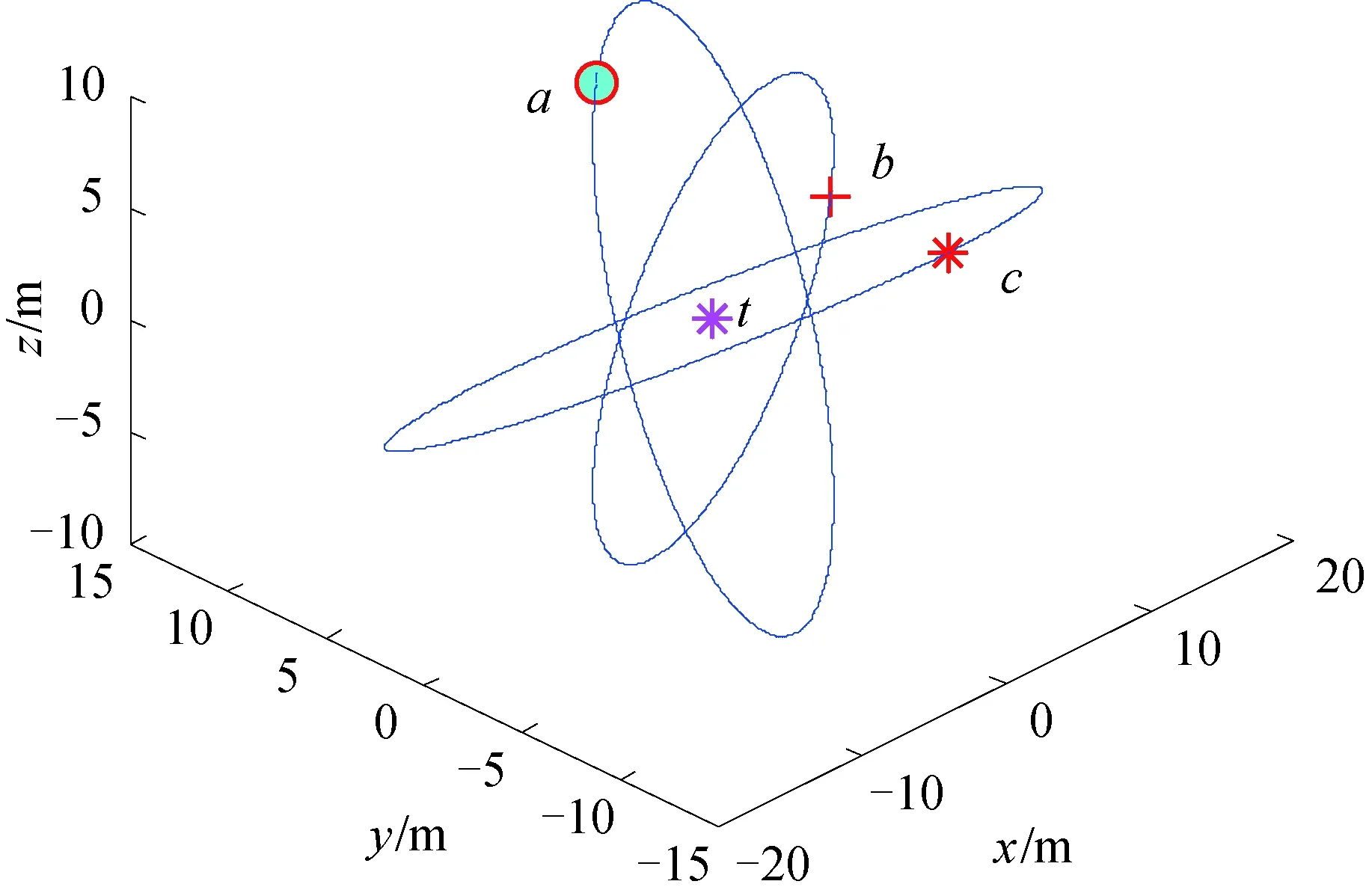
图4 3颗观测卫星3轨道运动轨迹Fig.4 Movements of three observation satellites in three orbits
2.2.3 6星3轨道观测
为满足实时、全覆盖观测的要求,设计位于3个轨道面的6颗卫星进行观测,同轨道2颗观测卫星间隔为180°,3个轨道面倾角间隔为45°(见图5)。图中:2颗观测卫星a的观测光轴对准空间目标左帆板的几何中心,2颗观测卫星b的观测光轴对准空间目标的几何中心,2颗观测卫星c的观测光轴对准空间目标t右帆板的几何中心。

图5 6颗观测卫星3轨道运动轨迹Fig.5 Movements of six observation satellites in three orbits
3 基于网格统计的详查任务分析
近距离绕飞详查的目的是获取空间目标尽可能多的图像信息,以构建空间目标精确的三维模型,从而支持后续的在轨操作任务。观测卫星在某一时刻只能观测空间目标表面的部分区域;经过一段时间观测后,覆盖率的计算依赖于对已观测区域的标识;而对空间目标表面实现最大覆盖详查的最短时间又依赖于覆盖率的计算。因此,需对绕飞详查过程中的覆盖区域进行统计。
点覆盖数值仿真是一种统计多颗观测卫星对观测区域覆盖特性的方法[10-11],其优点是考虑了各种轨道及摄动影响,缺点是计算量大。将点覆盖数值仿真应用于在轨近距离详查任务分析,对空间目标的表面进行网格离散,由各颗观测卫星在不同时刻、状态下对空间目标表面区域内的网格进行标识与统计,分析三维观测绕飞详查任务的覆盖率变化。
3.1 区域网格空间划分
根据任意区域的目标R各顶点的最小值、最大值(Xmin,Xmax,Ymin,Ymax),定义1个矩形区域,目标区域位于矩形区域的内部,将该目标区域在X,Y轴方向上分割成连续的相邻网格,如图6所示。
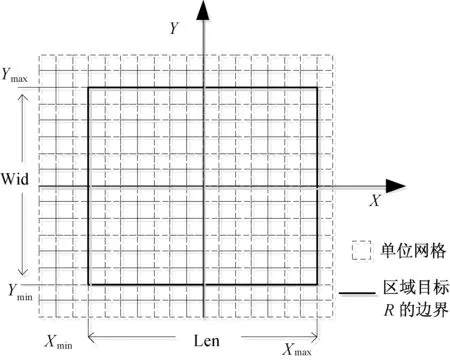
图6 网格统计法示意图Fig.6 Schematic diagram of grid statistics
图6中网格组成的集合为网格空间,记为
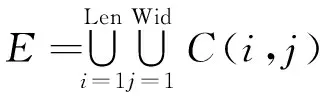
(11)
式中:Len,Wid分别为X,Y轴方向上的网格数;i,j分别为X,Y轴方向上的网格编号;C(i,j)为单位网格。
对于长方体目标,本文将6个表面分为6个矩形区域,分别对每个区域进行网格划分,且网格中心点的位置坐标选用空间三维坐标值表征。当网格划分足够精细时,可用单位网格的中心点来表征整个单位网格的观测情况。
对于点目标,本文将其单独构成1个不存在面积的单位网格,具体表示为
C(i,j)={N(i,j);P(i,j);S(i,j)}
(12)
式中:i≤Len;j≤Wid;N(i,j)为网格编号;P(i,j)为点坐标;S(i,j)为网格覆盖状态,其表达式为

(13)
3.2 基于网格统计的分析
假设目标区域内的每个网格只需被观测1次,则当所有网格均观测至少1次便实现了全覆盖。对于任意网格C(i,j)∈Er且网格覆盖状态值S(i,j)=0,当目标区域首次被观测时,S(i,j)变为1。每项观测任务执行完毕后,网格空间进行更新,被观测后S(i,j)为1的网格相当于待观测区域“外”部分。因此,下一步观测是对更新后未观测的网格空间进行分析,从而避免重复统计,提高观测计算效率。
基于上述规则,将已观测的目标区域覆盖率表示为
R=E/V
(14)
式中:V为目标区域内划分网格点的总数,V=Len×Wid;E为目标区域内覆盖状态为1的网格点数量。
在相对坐标系下,对空间目标表面进行区域网格划分预处理,以观测卫星运动状态为观测基点,对空间目标表面进行判断,统计覆盖特性。具体流程如图7所示。

图7 覆盖特性计算流程Fig.7 Calculation flowchart of coverage characteristics
3.3 近距离三维详查任务分析
根据2.2节中设计的观测任务,通过实施不同观测策略对简化的空间目标进行详查,统计观测结果,分析最大覆盖率、最大覆盖时的最短绕飞时间等覆盖特性。
当观测卫星对空间目标主体(非旋转目标)观测时,随着绕飞距离的增大,观测视场变大,可观测区域放大;同时,可观测部分在1个绕飞周期后重复。对于不同绕飞距离,计算绕飞1个周期内的最大覆盖率;对统计过程中覆盖率达到1的情况,计算达到最大覆盖的最短绕飞时间。
当观测卫星对空间目标太阳帆板(旋转目标)观测时,可观测部分随时间变化,如果可对旋转目标全覆盖观测,则计算最大观测的最短绕飞时间;如果不能对旋转目标全覆盖观测,则计算绕飞2个周期时的最大覆盖率。
4 算例分析
4.1 参数设置
空间目标主体和太阳能帆板的尺寸见表1。在相对坐标系下,单颗观测卫星的初始位置参数为:绕飞半径A=1 m,k=1.5,φ=0°,φ=0°,ωn=9.918×10-4rad/s,绕飞周期T=6 335 s,星载遥感器视场半锥角Δg=5°。当A以0.5 m的步长从1 m增加到20 m时,分析覆盖率R及最大覆盖时的最短绕飞时间tk的变化规律。
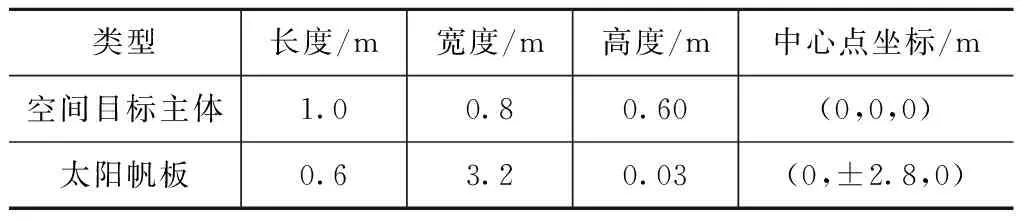
表1 模拟空间目标尺寸
4.2 仿真结果
4.2.1 单卫星观测
单颗观测卫星观测时绕飞距离与覆盖特性的关系如图8所示。图8(a)为观测光轴固定的情况,由图可见:随着绕飞半径的增大,覆盖率呈近直线增加,直到全覆盖(覆盖率为1),之后覆盖率不变;最大覆盖最短绕飞时间随着绕飞半径距离的增大而减小,绕飞半径达到一定距离后,最大覆盖的最短绕飞时间不再变化。图8(b)为光轴匀速转动的情况,达到最大覆盖的最短绕飞时间更短,最小绕飞半径更小。考虑到观测光轴固定,太阳帆板静止不动情况,实现全覆盖观测的绕飞半径需大于24.5 m,约为旋转太阳帆板刚达到全覆盖时绕飞半径的2倍,且其最大覆盖时的最短绕飞时间约为旋转太阳帆板的3倍,综合空间内实际的工作卫星,本文主要分析太阳帆板旋转条件下的观测情况。
4.2.2 3轨道3卫星观测
3轨道3颗观测卫星的观测分析结果如图9所示。由图可见:多颗卫星观测时覆盖率明显提高,最大覆盖的最短绕飞时间缩短。对空间目标主体最大覆盖时的最短绕飞时间从绕飞半径大于5 m后几乎不变,对空间目标太阳帆板最大覆盖时的最短时间从绕飞半径大于10 m后保持不变。分析空间目标主体、太阳帆板的特点,瞬时状态下单颗卫星单独观测不能全覆盖观测目标,空间目标主体的结构原因导致单颗卫星观测长方体需要有一定的最短绕飞时间,空间目标太阳帆板的最短绕飞时间很短是由于帆板很薄且帆板自身的转动加快了观测卫星的实际相对角速度。

图8 单星绕飞距离与覆盖特性的关系Fig.8 Relationship between fly-around distance and coverage characteristics of single observation satellite
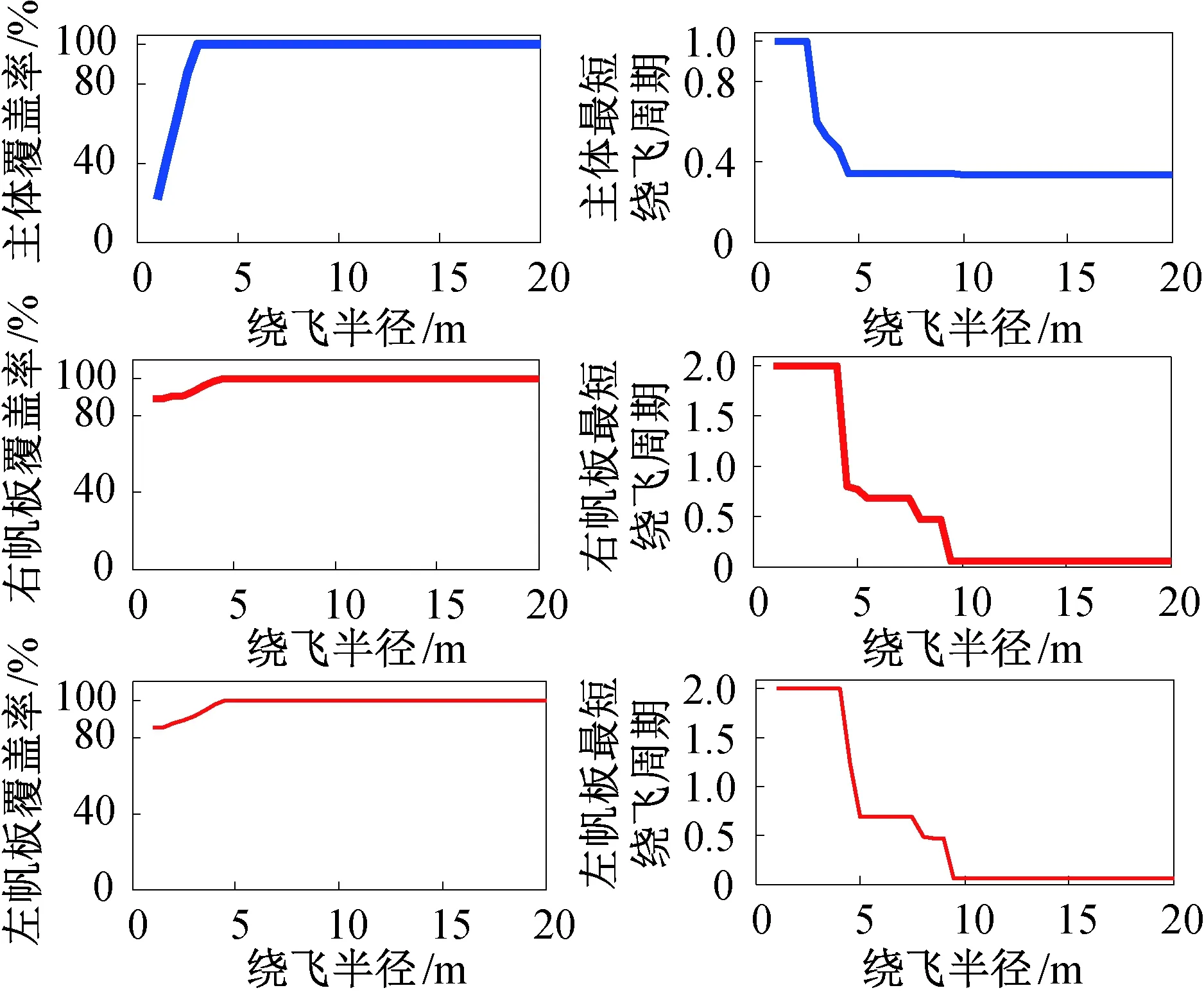
图9 3星绕飞距离与覆盖特性的关系Fig.9 Relationship between fly-around distance and coverage characteristics of three observation satellites
4.2.3 3轨道6卫星观测
3轨道6颗卫星的观测分析结果如图10所示。由图可见:当绕飞距离大于10 m时,卫星可在某时刻达到全覆盖观测,实现全方位、实时观测。实际任务中,绕飞半径小有利于获得高分辨率图像,但目标本身具有一定尺寸,绕飞半径小过小容易造成碰撞事故,因此需根据实际情况确定绕飞半径。

图10 6星绕飞距离与覆盖特性的关系Fig.10 Relationship between fly-around distance and coverage characteristics of six observation satellites
4.3 比较分析
由图8(b)可见:当单颗观测卫星光轴转动观测太阳帆板结构时,在观测卫星绕飞半径大于6 m后实现对目标的全覆盖观测。由图9可见:多颗观测卫星同时观测目标主体,当观测卫星绕飞半径大于3 m时,可实现对空间目标的全覆盖观测;由图10可见:当观测卫星绕飞半径大于4.5 m时,可实现瞬时全覆盖观测。
本文将目标结构、卫星资源、安全性等条件,与实时、全覆盖观测的任务要求相结合,减少观测卫星数量以节约资源。空间目标主体为长方体结构,功能多样。为满足实时全方位覆盖的任务要求,应配置至少由3颗观测卫星进行实时观测,绕飞半径至少为8 m。由于空间目标的太阳能帆板结构简单,设计1颗绕飞半径为10 m的观测卫星b对其进行观测,观测光轴随时间变化而转动,且1个周期内沿y轴从空间目标左帆板的最左端匀速转移到右帆板的最右端。
仿真验证本文所设计的4颗卫星、4个轨道面的编队(见图11),可使空间目标主体在某时刻被全覆盖观测,且满足空间目标太阳能帆板在1个周期内被全覆盖观测的任务要求。

图11 4轨道4颗观测卫星运动轨迹Fig.11 Movements of four observation satellites in four orbits
5 结束语
本文采用网格点仿真方法,对多颗观测卫星近距离详查空间目标的任务进行设计和分析,结果表明:最大覆盖的最短绕飞时间随着绕飞距离增大呈阶段性减小;采用观测光轴转动策略与多颗观测卫星编队观测策略均可实现全覆盖观测。在相同绕飞半径条件下,多颗卫星编队协同观测的任务特性明显优于单颗卫星单独观测,因此,设计合理的编队构型,如4颗卫星4个轨道面的绕飞编队构型,可获得详细完整的目标信息,实现全方位、实时观测,既可节约资源,又能提升经济效益,提高任务成功率。
本文假设空间目标为简单的长方体与平面板结构相结合,但实际空间目标主体的构型更为复杂,需考虑目标整体形貌,以及帆板、杆系、喷管、天线等局部特征的识别等,因此将对更复杂构型空间目标的三维详查任务进行研究。本文假设观测卫星为质点,实际情况下如果观测卫星绕飞半径太小,存在观测卫星与空间目标、观测卫星与观测卫星之间碰撞的风险,因此将深入研究多颗观测卫星近距离操作碰撞规避的问题。

