五棱锥SGCMGs失效时奇异构型几何分析及操纵律设计

王焕杰，刘 禹，张召弟

(1.上海航天控制技术研究所，上海 201109； 2.上海市空间智能控制技术重点实验室，上海 201109)

0 引言

单框架控制力矩陀螺(SGCMG)作为一种角动量交换装置，凭借其大力矩输出特性，在航天器姿态控制领域被广泛应用[1]。SGCMG在进行三维力矩输出时，多以3个或3个以上成簇组成一定构型。根据所选SGCMG个数及其安装方式不同将其分为平行构型和独立构型。常见的独立构型有双平行构型、三平行构型；独立构型有金字塔构型、五棱锥构型等。文献[2]介绍了各类构型的分类。文献[3]分析了SGCMGs构型的几何特性，并给出了各SGCMGs构型奇异点的理论推导。

基于不同的SGCMGs构型，学者们设计了不同的操纵律，当前操纵律的设计问题主要集中在对雅克比矩阵求逆上。其中最简单的是伪逆操纵律[4]，此操纵律虽然能得到精确解，但却无奇异规避能力。带零运动的伪逆操纵律[5]和鲁棒伪逆操纵律[6]是对伪逆操纵律的改进，都在不同程度上实现了对奇异状态的回避。带零运动的伪逆操纵律能有效避免构型的内部隐奇异点，但无法解决内部显奇异问题；鲁棒伪逆操纵律在进行奇异规避的同时会引入误差项，降低控制精度。以上提到的操纵律都是针对某类构型而言，不具备研究的一般化特性。

五棱锥构型由于其内部显奇异点靠近包络，已成功应用于“和平号”空间站[7]，但其所采用的带有零运动的伪逆操纵律具有较强的针对性，对内部奇异复杂的构型并不适用。五棱锥SGCMGs单只失效后，内部奇异点分布情况复杂，具备研究的一般化特性。针对此类奇异点的复杂构型，多采用引入扰动的方法进行奇异规避。文献[8]采用一种变系数的鲁棒伪逆操纵律，文献[9-10]采用一种引入附加框架加速度的方法，都实现了对奇异的规避，但均未对构型内部的显奇异点和隐奇异点加以区分。如何在有效规避奇异的基础上尽量实现指令力矩的精确输出，是SGCMGs使用研究的重点。从工程应用的角度出发，往往通过引入一定的摄动来保证SGCMGs的有效规避，这就意味着SGCMGs输出了指令力矩之外的干扰力矩。随着航天器高精度姿态控制要求的提高，这些干扰力矩需要尽量减小甚至避免。

本文以五棱锥构型为例进行构型分析，对单只陀螺完全失效后构型的内部奇异情况进行了研究，重点对失效前后显奇异点、隐奇异点的分布进行了分析及量化对比。同时针对单只陀螺失效后，构型具备的一般化奇异特性，综合零运动规避隐奇异和鲁棒伪逆规避显奇异的优点进行了操纵律设计，在保证奇异规避的基础上有效减小了干扰力矩。最后，采用单只陀螺失效后的五棱锥SGCMGs构型，以三轴姿态机动任务为例，对所设计的操纵律和传统的鲁棒伪逆操纵律进行了仿真。

1 构型分析

五棱锥构型[11]采用6个SGCMG进行独立型方式安装，其中5个被分别安装在正五棱锥体相邻的5个侧面，另一个沿五棱锥的中轴线方向安装，任意相邻两面的夹角为116.51°。各陀螺的框架轴对称分布，分别垂直于其所在侧面，锥面与地面夹角为β=63.4°。系统构型如图1所示。

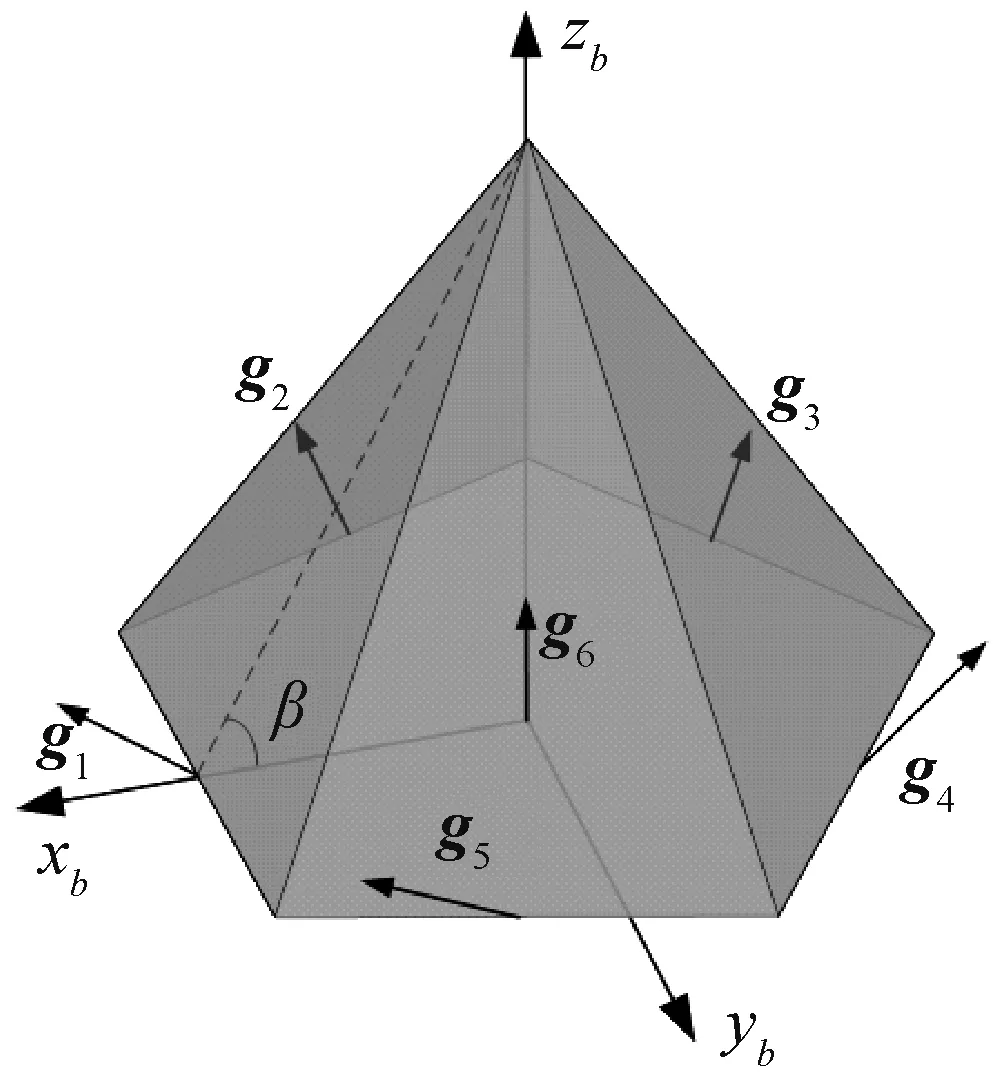
图1 五棱锥构型示意图Fig.1 FPC configuration diagram

各框架轴的安装方向分别为

(1)

根据SGCMG单元的力矩输出特性，其角动量hi、输出力矩ci与框架轴安装方向gi两两垂直。在确定框架轴安装方向后，对应不同的SGCMG框架转角可求得每个SGCMG的角动量，进而可求得SGCMGs构型的角动量

(2)

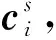
(3)

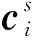
(4)

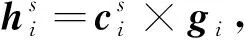
(5)

总的奇异角动量

(6)

由此可得构型的角动量奇异面，如图2所示。该奇异面包含显奇异点和隐奇异点，针对每个奇异点，判断其有无零运动存在[12]。1个奇异点若存在零运动，为隐奇异点，如图3所示；反之则为显奇异点，如图4所示。图中的Hx、Hy、Hz分别表示角动量在x、y、z轴的分量。

图2 五棱锥构型奇异面Fig.2 FPC singular surface

图3 五棱锥构型隐奇异面Fig.3 FPC passable singular surface

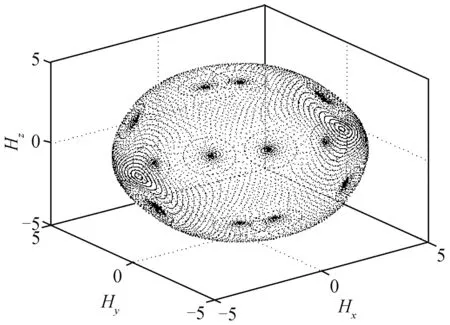
图4 五棱锥构型显奇异面Fig.4 FPC impassable singular surface

考虑到五棱锥构型的强对称性，单只陀螺失效情况以CMG1和CMG6失效为例进行分析，本文只对CMG1失效后构型的奇异面、隐奇异面、显奇异面进行超曲面输出，如图5～7所示。

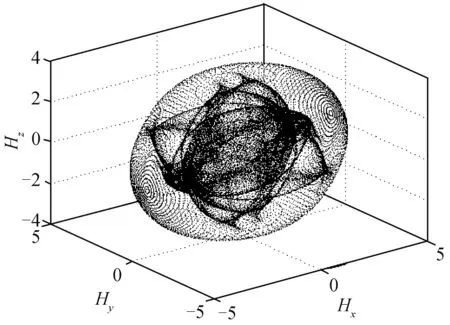
图5 CMG1失效后奇异面Fig.5 Singular surface after CMG1 is invalid

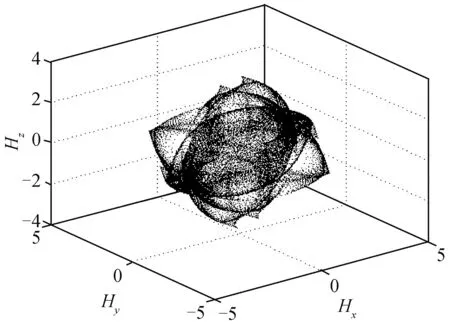
图6 CMG1失效后隐奇异面Fig.6 Passable singular surface after CMG1 is invalid

图7 CMG1失效后显奇异面Fig.7 Impassable singular surface after CMG1 is invalid

通过比较得到单只陀螺失效前后构型奇异面的几何特性，见表1。

表1 失效前后构型角动量情况

用文献[13]中的4个性能参数表示构型特性，如下所示：

1) 构型效益。SGCMGs角动量包络面上的最小值与SGCMGs角动量代数和之比，表征了单个SGCMG对整个构型贡献的大小。值越大表明单个SGCMG发挥的作用越大。

2) 构型效率。角动量体包络面上的最小值与最大值之比，值越大表明构型的角动量体越接近球状，构型在各方向能够提供的力矩输出能力越均衡，对工作环境的适应能力也越强。

3) 可控效益。SGCMGs构型最小显奇异点角动量与SGCMGs角动量的代数和之比。以最小显奇异点为半径的开球所表示的角动量体内不会遭遇显奇异问题，而隐奇异可通过零运动脱离，所以值越大表明系统规避奇异的能力越强，控制能力越强。

4) 奇异点损失率。构型效益与可控效益的差值，值越小表明构型显奇异点越接近包络面附近，构型的可控角动量球也就越大。

失效前后构型性能参数汇总见表2。

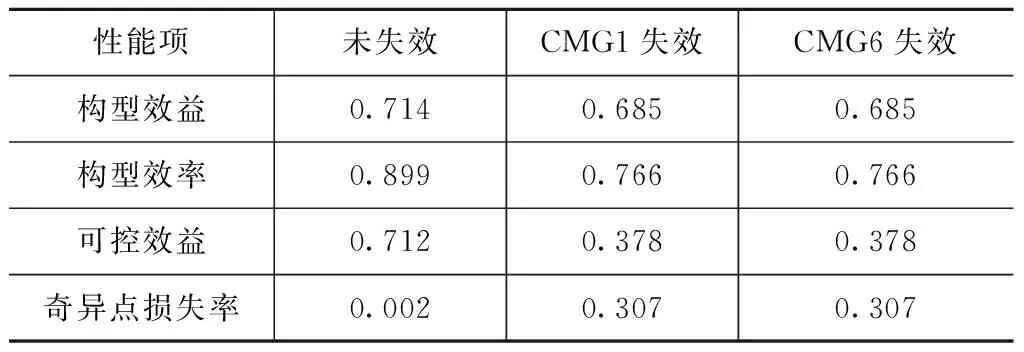
表2 失效前后构型性能参数

通过比较发现，CMG1和CMG6失效后构型变化情况相同，如下所示：

1) 构型角动量体包络减小，构型效益下降，表明角动量体减小，最大输出能力下降。

2) 包络最大角动量与包络最小角动量相差增大，构型效率下降，表明角动量体偏离球形，构型在三轴方向的力矩输出能力均衡度变差。

3) 最小显奇异点远离包络，可控效益大幅下降，奇异点损失率大幅上升，表明显奇异点内切球(球内无显奇异点)半径大幅减小，可适用零运动的角动量球缩小。

2 操纵律设

五棱锥构型中，半径为4.27h0的角动量球内只有隐奇异点存在。针对隐奇异点可通过零运动规避的特性，文献[11]采用“伪逆+零运动”操纵律，这一操纵律对此类显奇异点内切球较大的构型具有明显的适用性，具体描述如下：

(7)

单只陀螺失效后带来的最明显变化是五棱锥构型内部奇异点组成的复杂化，失效后该半径迅速下降至1.889h0。若仍旧采用“伪逆+零运动”操纵律，则将工作空间限制在该内切球内，一旦超出该球范围极有可能遭遇显奇异点，而“伪逆+零运动”显然不具备规避显奇异点的能力。对于这类显奇异点深入角动量体内部的构型，文献[6]设计了摄动鲁棒伪逆操纵律，如下所示：

(8)

式中：λ为正误差项系数；I3×3为单位阵；E3×3为摄动矩阵,其中

(9)

式中：εj为适当选取的小量，εj=0.01sin(0.5πt+φj)(j=1，2，3)。相位差分别为φ1=0，φ2=0.5π，φ3=π。

该操纵律通过引入误差摄动项进行奇异规避，对显、隐奇异点均适用，但由于引入误差项会带来额外的误差力矩输出，不利于高精度的姿态控制。

基于以上2种操纵律的优缺点，本文设计了一种带零运动的鲁棒伪逆操纵律。设计的基本思路为：在角动量向奇异点逼近的过程中，优先将此奇异点作为隐奇异点处理，引入零运动进行规避，若奇异状态未恶化至阈值状态(σ≥σ1)时，仍将此点作为隐奇异点处理；当奇异情况进一步恶化，奇异值低于阈值(σ<σ1)时，表明零运动效果不佳，此时将奇异点作为显奇异点处理，引入摄动项进行规避。具体形式为

(10)

系数λ，α选取规则为

(11)

当构型大于奇异度量阈值σ1时，优先对内部隐奇异点进行规避，此时求解准确，不引入误差项；当构型奇异度量小于σ1时，表明零运动作用不大，此时引入摄动项，为避免指令框架角速度过大，将零运动项置零。这样能在充分利用内部隐奇异点的基础上实现对显奇异点的规避。选取阈值σ1时不宜过大，阈值越大表明零运动作用的区间越小，摄动工作区间越大。阈值选取原则为：在尽量扩大零运动作用区间的同时，保证摄动能及时规避显奇异点。

3 平台动力学建模

为验证操纵律的控制效果，建立以SGCMGs为执行机构的卫星姿态动力学模型，有

(12)

式中：J为包含SGCMGs在内的整星惯量阵，J=Jb+JCMG；h为SGCMGs构型角动量；ω为卫星本体相对惯性系的角速度；Tc为SGCMGs输出力矩；Te为外部力矩[14]。

采用四元数描述卫星的运动学方程，有

(13)

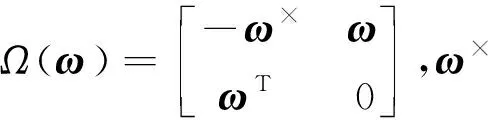
4 仿真分析

设飞行器相对质心坐标系的惯量为

Jb=diag(4 000 3 000 3 000)kg·m2

单个SGCMG的角动量h0=25 N·m·s，最大力矩输出为10 N·m。卫星初始三轴惯性姿态角均为1°，三轴角速度均为0.1 (°)/s，三轴外部干扰力矩为1 mN·m。采用5次多项式法设计一种三轴姿态机动标准轨迹，轨迹时长80 s，机动角度0°。喷气卸载触发条件为

(14)

以CMG1失效为例，分别采用鲁棒伪逆操纵律和带零运动的鲁棒伪逆操纵律进行仿真。

图8～10分别为三轴跟踪标准轨迹进行姿态机动的姿态角曲线，可以发现在40 s左右采用鲁棒伪逆操纵律得到的三轴机动曲线明显偏离标准轨迹，偏差为2°以上。结合图11可知，这是由于喷气卸载干扰造成的，卸载结束后，曲线逐渐收敛。而采用带有零运动的鲁棒伪逆操纵律机动效果明显优于前者，实时跟踪精度能达到0.01°以上。

图8 滚动角机动曲线Fig.8 Roll angle maneuvering trajectory

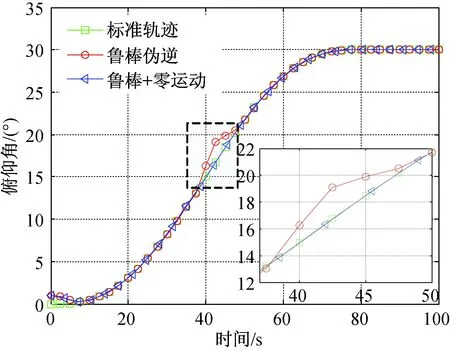
图9 俯仰角机动曲线Fig.9 Pitch angle maneuvering trajectory

图10 偏航角机动曲线Fig.10 Yaw angle maneuvering trajectory

图11 喷气卸载力矩Fig.11 Jet unloading torque

结合喷气卸载力矩、构型角动量及构型奇异度量，可以得出：采用鲁棒伪逆操纵律在机动过程中虽然避免了内部的奇异状况，但由于摄动的影响造成额外的力矩输出，在40 s前后角动量约为80 N·m·s，且奇异度量在接近0.2时触发喷气卸载，造成跟踪误差增大。而采用带有零运动的鲁棒伪逆操纵律充分利用了角动量体内部的隐奇异点，奇异度量始终保持在0.5以上，表明构型始终远离奇异状态。

图12 构型角动量曲线Fig.12 Configuration angular momentum curve

图13 构型奇异度量曲线Fig.13 Singularity index curve

5 结束语

本文针对五棱锥SGCMGs构型及单只陀螺失效情况下的内部奇异状况进行了几何分析，并计算得到了一系列的性能参数。基于单只陀螺失效后内部奇异的复杂情况，在前人研究的基础上设计了一种适用于显奇异点深入角动量体SGCMGs构型的综合操纵律，在规避显奇异点的基础上充分利用内部的隐奇异点。通过仿真比较发现，本文设计的综合操纵律控制效果优于传统的鲁棒伪逆操纵律。该设计的操纵律结合了鲁棒伪逆和带零运动的伪逆操纵律的优点，对于内部显奇异点进行摄动规避，隐奇异点进行零运动规避，在规避奇异方面具有一定通用性，同样适用于金字塔型、双平型等多种SGCMGs构型，在工程上具有一定的实用性。

本文通过阈值的选取将角动量工作空间划分两部分(σ<σ1和σ≥σ1)，未考虑两者间的过渡区域。后续可在考虑SGCMG最大框架角速度的前提下，增加σ1的过渡部分，通过优化参数配置实现零运动的伪逆操纵律向鲁棒伪逆操纵律的小扰动过渡。