一种基于机动辨识预测的空空导弹导引律

常立凡，任高峰，胥 彪，李 爽

(1.南京航空航天大学 航天学院，江苏 南京 210016； 2.中国空空导弹研究院，河南 洛阳 471009)

0 引言

目前各国空空导弹大多采用比例导引律，其结构简单，对低机动目标打击效果较好[1-3]。考虑到新一代目标的机动能力更强[1-3]，国内外学者提出了一些修正形式的比例导引律[4-5]。如：侯明善等[6]设计了一种非线性状态估计器，其利用导引头信息估算出弹目视线角，并对比例导引系统进行补偿，与传统比例导引率相比，指令加速度更小，弹道特性更好；GURFIL[7]针对大机动目标提出一种基于零脱靶量修正的比例导引律，其零脱靶量是基于随机过程建立的目标机动模型，制导精度取决于目标实际机动情况与模型的匹配度；周华等[8]提出了一种针对机动目标时间可控的协同制导律，其由时间误差反馈、引入目标机动补偿的扩展比例导引结合推导得出，结构简单，易于实现。

目标模型是目标估计算法的基础，目前典型模型有Singer、Jerk、“当前”统计(CS)等。其中，CS模型最为常用[9],该模型认为当目标以某一加速度机动时，下一时刻的加速度取值有限，且只能在当前加速度范围内。CS模型本质上是一种时间相关模型，机动目标“当前”加速度的预测值即为均值[10]。白亚腾等[11]在CS模型和扩展卡尔曼滤波(EKF)算法基础上提出一种基于状态噪声方差自适应(SNVA)的机动目标状态估计方法，利用位置预测值与位置估计值之间的偏差对加速度方差进行自适应调节，采用SNVA对目标加速度噪声方差进行自适应调整，并通过EKF算法估计目标速度和加速度，所得精度较高；戚靖等[12]对CS模型机动频率进行了自适应调整，提出了一种改进的匀速运动(CV)模型，弥补了CS模型在弱机动情况下跟踪精度不高的缺点；CHEN等[13]针对抗大机动目标的制导问题提出了一种基于模型的方法，该方法对目标套用1个振幅和频率未定的三角函数模型，包括1个可变增益的卡尔曼滤波器，以估计相对位置、相对速度、加速度的幅值和频率，再利用组合导引律根据目标状态估计来发出导弹的加速度指令，但该方法估计过程具有明显的延迟；王利芳等[14]设计了一种评估目标机动意图的算法，将目标机动意图分为9种类型,根据所测量、估计的目标运动参数，提取目标特征参数，判断目标威胁，评估机动意图，该方法流程简单，判断过程易于实现。

上述方法仅将目标机动描述为与时间相关的随机过程，使用的模型种类较少，并没有研究各种典型的规避动作。由于单个模型适用范围有限，无法涵盖一些特殊的机动情况，当目标进行模型库以外的机动时，会有较大的估计误差，造成制导精度严重下降。为此，本文调研了以第五代战斗机为主的高机动目标在规避导弹时所使用的典型规避机动形式，建立运动学模型，构成了可扩展的目标机动轨迹离线模型库，并在此基础上构建了卡尔曼滤波器，根据模型库的函数类型特征设计了目标机动辨识预测器，对目标进行机动辨识与预测，规定了数据采样的法则、机动辨识的标准和延迟补偿的算法，针对三角函数拟合的缺点，优化了函数次序，优先拟合低阶函数，在线判断目标所处的机动状态及相关机动参数，并给出预测位置。

1 基本模型

在建立导弹目标模型时，假设导弹与目标的速度保持不变，导弹为可控质点，则弹目之间的三维相对运动模型如图1所示。

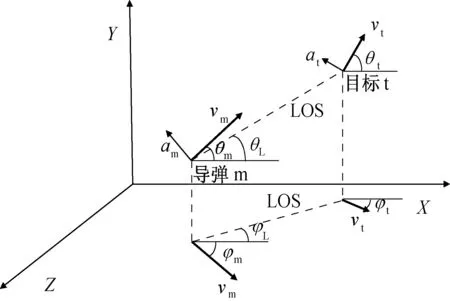
图1 导弹、目标追击三维模型Fig.1 3D model of missile and target

图1中：

(1)

为便于描述目标各种机动动作并以此建模，选取地理坐标系(O-XYZ)为基准。该坐标系原点为导弹发射点在当地水平面上的投影点，OX轴沿原点所在纬线的切线方向指向东方，OZ轴沿原点所在经线的切线方向指向北方，OY轴根据右手定则指向天。

2 机动描述与模型建立

在空战中，战斗机可根据局势进行机动以规避来袭导弹。随着战斗机气动设计和发动机性能的改进，现有空空导弹的制导律难以有效打击高机动目标，因此，需对高机动目标的具体特征进行详细建模，设计相应的导引律。本节针对一些典型的战斗机规避动作进行分析研究，根据典型的目标机动特征建立运动学模型。机动模型库中使用的模型如图2所示，均以X轴为前进方向。当目标执行模型库以外有规律机动时，可离线补充新的机动模型。

2.1 加速机动

加速机动是最简单的规避机动。目标发现导弹来袭后，一般会增大节流阀以获得更快速度，为后续的大过载规避机动进行准备。该机动在X轴有加速度a1，在Y、Z轴没有速度和加速度。机动模型的加速度可描述为

(2)

式中：x，y，z分别为目标坐标值。

当目标在Y，Z轴的分速度为0 m/s时，对应的目标速度表示为

(3)

目标的机动轨迹可描述为

x=0.5a1t2+v1xt+x0，y=y0，z=z0

(4)

式中:x0,y0,z0为目标初始位置；v1x为初始时刻的目标速度；t为时间。

2.2 盘旋/筋斗机动

盘旋机动为一类常见的平面机动，其飞行轨迹在机动平面内近似为圆形，其机动平面平行于当地水平面。筋斗机动的机动平面垂直于当地水平面。这2种机动可维持较长时间的横向加速度，在末制导段利用超强的机动性强行避开导弹的杀伤区，此外，在中制导段可利用该机动消耗空空导弹的能量，使其在进入末制导时速度不足。盘旋/筋斗机动模型如图2(a)所示。

盘旋机动是平面机动，在Y轴没有速度和加速度，其轨迹为圆形。假设在机动平面内的加速度为a2，则各轴加速度为

(5)

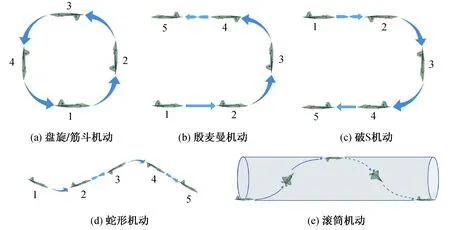
图2 机动模型Fig.2 Maneuver models

式中：ω，ω0分别为目标的机动频率、初相位。X，Z轴的偏置速度一般为0，对应的目标速度为

(6)

在盘旋机动中，v1x，v1z一般为0，其机动轨迹表示为

(7)

筋斗机动相当于把盘旋机动的平面换成XOY平面。

2.3 殷麦曼/破S机动

殷麦曼机动、破S机动用于动能与势能之间转换，两者类型相同，方向相反，初始状态均为平飞。殷麦曼机动先完成半个周期的筋斗机动，此时飞机状态为倒飞，然后滚转半周改为平飞，损失速度以获得高度；破S机动先滚转半周进入倒飞，然后完成半周的筋斗机动，最后改为平飞，损失高度以获得速度。殷麦曼/破S机动为平面机动，相当于筋斗机动执行半个周期(初始状态为平飞)，模型如图2(b)、(c)所示。

2.4 蛇形机动

蛇形机动既可保持可观的前进速度，又能产生一定的横向加速度，其周期和幅值有较大的调节空间，机动轨迹在空中为“S”形。蛇形机动操作复杂，每半个周期需通过滚转来改变机动方向，此时目标横向加速度较小，易受到攻击。蛇形机动的模型如图2(d)所示。

蛇形机动在XOZ平面内，目标沿X轴匀速前进，同时沿Z轴正弦运动，假设最大加速度为a3，在Y轴没有速度和加速度，则加速度可描述为

(8)

一般来说，目标在X轴有初速度v3x，在Z轴的偏置速度为0，则对应的速度为

(9)

蛇形机动的轨迹可描述为

(10)

2.5 滚筒机动

滚筒机动是最有效的导弹防御机动之一，其轨迹为1条螺旋线，既能像蛇形机动那样在前进中保持较高的横向加速度，又能克服蛇形机动操作复杂的缺点。滚筒机动的周期取决于目标的滚转周期，略长于目标滚转1周的时间。滚筒机动的横向过载方向随时间快速变化，可针对导弹制导系统有时间延迟的缺陷，使导弹制导系统反复改变指令。当指令变化频率超过系统带宽时，导弹舵面无法及时跟踪制导系统的加速度指令，造成动态误差不断增大，最终导致导弹脱靶。滚筒机动模型如图2(e)所示。

滚筒机动可分解为沿X轴的直线前进和在YOZ平面内的圆周运动，在Y、Z轴进一步分解可得到2个正弦轨迹。假设在机动平面内的加速度为a4，则各轴加速度可描述为

(11)

一般来说，目标在X轴的初速度为v4x，在Y、Z轴的偏置速度为0，对应的目标速度为

(12)

滚筒机动的轨迹为

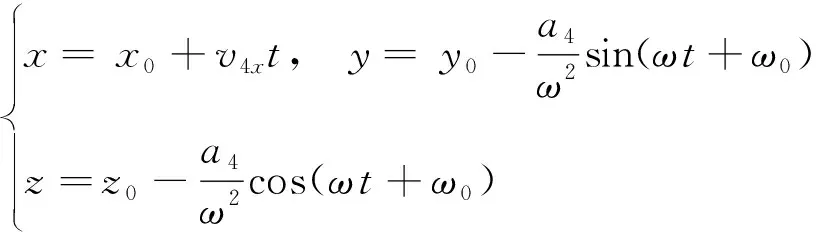
(13)

3 带预测的制导与控制

3.1 导弹导引律

采用现役主动寻的空空导弹常用的比例导引律，将导弹姿态角速度与弹目视线角速度的比值作为比例系数，俯仰控制和偏航控制相互独立，其公式为

(14)

(15)

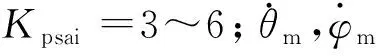
3.2 卡尔曼滤波器

机动目标状态的位置向量为

X=[xyz]

(16)

式中：x，y，z分别为目标在X，Y，Z轴上的位置。根据卡尔曼滤波模型，机动目标的离散状态方程为

X(k+1)=F(k)X(k)+Q(k)

(17)

式中：Q(k)为零均值高斯白噪声；F(k)为状态转移矩阵。由于离散间隔很短，目标机动状态未知，默认下一时刻的位置不变，即

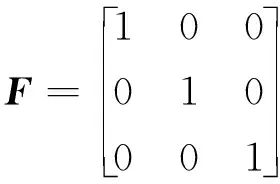
(18)

假设机动目标的测量方程为

Z(k)=H(k)X(k)+R(k)

(19)

式中：H(k)为测量矩阵；R(k)为测量过程中的高斯白噪声，则状态的一步预测为

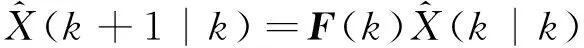
(20)

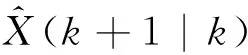
测量的预测值为

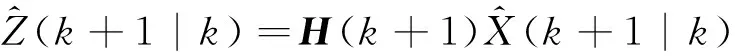
(21)

协方差的一步预测为

P(k+1|k)=F(k)P(k|k)F′(k)+Q(k)

(22)

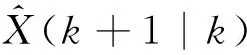
卡尔曼滤波增益为

K(k+1)=P(k+1|k)H′(k+1)/

[H(k+1)P(k+1|k)H′(k+1)+

R(k+1)]

(23)

校正后的最优估计为

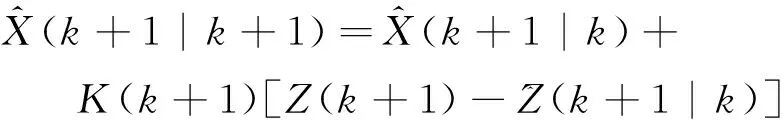
(24)

协方差更新为

P(k+1|k+1)=

[1-K(k+1)H(k+1)]P(k+1|k)

(25)

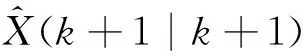
3.3 引入渐消因子的扩展卡尔曼滤波器

经典卡尔曼滤波器具有记忆无限增长的特点，当前滤波值会使用之前所有数据，这些数据逐渐积累，使新测量值对最优估计值的修正能力逐渐下降。当目标改变机动状态时，经典卡尔曼滤波器会导致较大的时间延迟和误差积累。因此，本文使用扩展卡尔曼滤波，在滤波时提高新测量数据的影响能力，避免旧数据的过度积累。

新的协方差预测公式为

P(k+1|k)=λkF(k)P(k|k)F′(k)+Q(k)

(26)

式中：λk为渐消因子，λk≥1。λk值使卡尔曼滤波的增益变大，增加了测量数据在计算状态估计时的权重，并因估算方法不同而有所区别。为此，徐定杰等[15]提出了一种基于新息的计算方法，其公式为

图3 导弹制导回路Fig.3 Missile guidance circuit

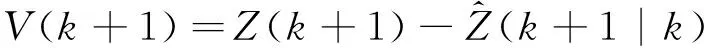
(27)

(28)

S(k+1)=H(k+1)P(k+1|k)

H′(k+1)+R(k+1)

(29)

(30)

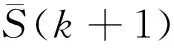
3.4 数据采样

数据采样需将导引头所获得的目标轨迹信息进行离散化，如果采样时间跨度过短，则难以提供有效的信息，曲率较高的轨迹会被识别成直线，而时间跨度过长则会失去时效性。考虑到现役高机动目标进行机动动作的周期为2～10 s，采集的时间跨度至少要达到机动周期的10%才能获得足够丰富的辨识信息。本文以0.1 s为时间间隔，采集最新的15个目标路径点，即时间跨度为1.4 s。在平衡信息量和时效性的同时，尽可能减小预测计算量。

3.5 辨识预测器设计

寻的系统生成目标数据具有时间延迟，导弹只能获得带时间延迟的目标信息,而目标机动预测器根据收集到的位置信息列表，对轨迹进行辨识，将辨识的结果和预测位置点传递给制导系统。当设计预测器时，对预测对象开展特征分析，对机动模型的轨迹进行统计，所统计的机动轨迹的函数类型见表1。

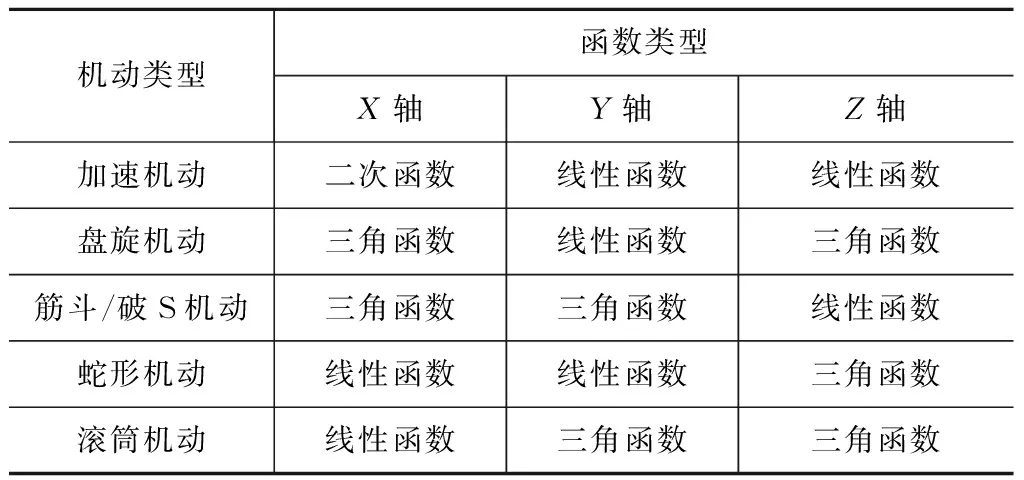
表1 机动轨迹的函数类型

利用最小二乘法对目标轨迹进行实时的函数拟合和在线辨识，可拟合的函数类型为线性函数、二次函数、三角函数。二次以上的函数虽然在理论上具有更小的残差，但在时间延拓时极易发散，故不予考虑。

线性函数的参数为

f(t)=A1t+A2

(31)

二次函数的参数为

f(t)=B1t2+B2t+B3

(32)

三角函数的参数为

f(t)=C1sin(C2t+C3)+C4

(33)

式(31)～(33)中：A，B，C分别为3种函数的参数。

对目标采用三角函数模型有一个显著的缺点：当目标进行匀速直线运动或机动加速度较小时，可能会造成较大的估计误差。三角函数模型误差如图4所示。由图可见：当目标沿平行于Z轴的直线匀速运动时，由于采样时间是等距的，在X、Y轴的坐标不变，在X-T图像中各采样点等距分布；在用三角函数拟合时，理论上振幅应为0，但由于振幅未作限制，会出现振幅为1个非零有限值的情况，以此参数进行预测时，得到的预测点会和实际点有较大偏差。在该情况下采用未知三角函数法预测虽然可将采样点的数据落在拟合的函数上，确保较小的残差，但预测精度明显不如线性函数拟合。当目标剧烈机动时，线性拟合的残差会加大，而未知三角函数法的表现较好。也就是说，采用三角函数拟合虽能辨识成功，但精度较差。为解决该问题，本文在函数拟合顺序上进行了优化：优先进行线性函数拟合，再进行二次函数拟合，最后进行三角函数拟合。当任意1项函数拟合满足辨识成功条件时，中止拟合，直到遍历所有函数类型。

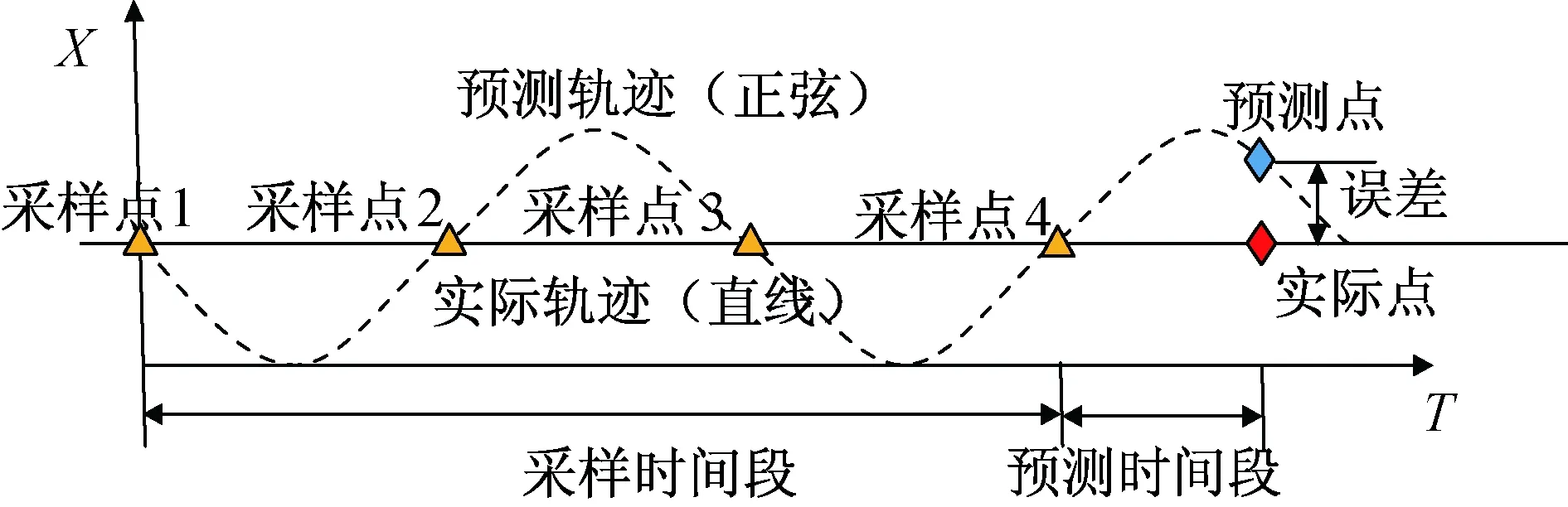
图4 三角函数模型误差Fig.4 Error of trigonometric function model

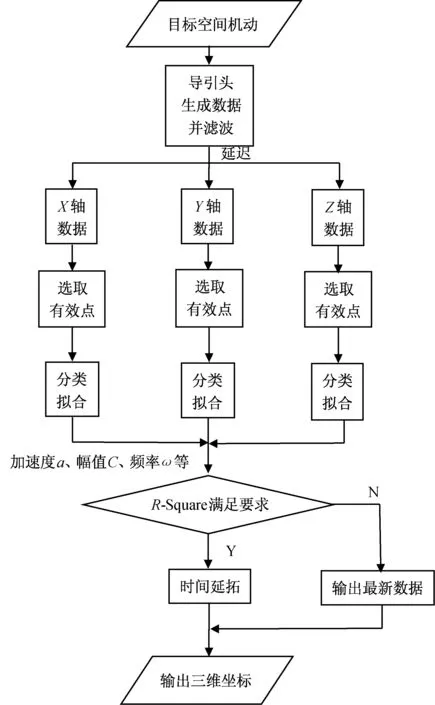
图5 辨识预测流程Fig.5 Flowchart of identification and prediction

辨识预测的流程如图5所示。辨识预测的具体步骤如下：

1) 当导引头检测到目标后，根据自身运动姿态，将位置坐标转换为绝对坐标系下的坐标，并生成随时间变化的列表，默认在中末制导中，导引头已锁定目标并保持稳定的跟踪。

2) 将数据列表在X，Y，Z轴方向上解耦，分解为3个数据列表。

3) 每个列表中以最新数据时间t，按照t-1.4，t-1.3，…，t的顺序，选取15个有效数据点，时间间隔0.1 s。

4) 将有效数据点进行拟合，根据机动模型库的内容，对数据点进行拟合与辨识。通过最小二乘法，将有效数据点在不同函数下进行拟合，并计算出拟合的确定系数(R-Square)，确定系数的计算公式为

(34)

式中：

(35)

(36)

RSST=RSSE+RSSR

(37)

RSSR为预测数据与原始数据之差的平方和；RSST为原始数据的方差；RSSE为拟合残差的平方和。

根据R-Square来判断此类拟合是否成功，线性函数和二次函数要求R-Square>0.992，三角函数拟合要求R-Square>0.984。若拟合成功，则输出函数类型和拟合参数；若模型库中所有函数类型拟合后均未成功，则判定辨识失败，输出失败标志。

5) 若辨识成功，则根据辨识成功的函数类型与参数，在最新的时间点后进行延拓，延拓的时间量等于导引头生成数据的延迟，这样理论上目标数据的延迟就能被机动预测器完全补偿；若辨识失败，则不进行时间延拓，仅输出最新的数据点。采样和预测的示意如图6所示。

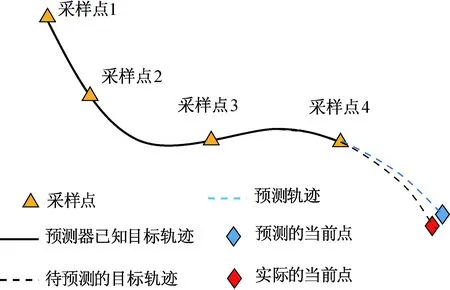
图6 采样与预测示意Fig.6 Schematic diagram of sampling and prediction

4 仿真算例

本文采用机动辨识预测制导律，对中低空的高机动目标进行模拟打靶，以验证新导引律的性能。目标的初始状态为匀速直线飞行，当发现来袭导弹后开始机动。导弹初始状态为xm0=0，ym0=1 km，zm0=0；目标初始状态为xt0=5 km，yt0=4 km，zt0=3 km。当仿真开始0～2 s后，导弹固连在载机上；仿真开始2～2.5 s后，导弹沿发射架飞出，发射方向角为30°，高度角为30°，发射后保持直线飞行，不受控制；当仿真开始2.5 s后，导弹根据控制系统的指令改变飞行轨迹，比例系数为4。导弹运动速度为300 m/s，目标进行直线巡航时速度为101 m/s，盘旋机动线速度为104 m/s，滚筒机动线速度为101.7 m/s。导引头测得目标实时位置在每个坐标轴均带有方差为3的高斯白噪声，获得目标信息并进行滤波的时间延迟共500 ms。作为对比，每个算例运行无预测比例导引和线性拟合预测比例导引(根据最新数据点的位置和速度，默认目标在带预测时间内保持匀速直线运动，以此补偿延迟)的仿真试验。3种导引律的目标预测方法如图7所示。无预测比例导引的目标预测点为最新采样点。以下3个算例对应3种典型的规避机动。

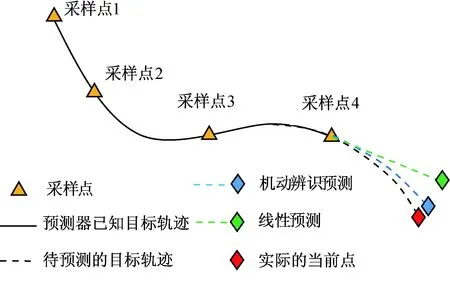
图7 3种预测点示意图Fig.7 Schematic diagram of three kinds of prediction points

4.1 盘旋机动

当仿真开始时，目标沿直线匀速巡航，高度角为-5.7°，方向角为185.7°。当仿真时间为12 s时，目标开始向左盘旋机动，过载为5.5g，盘旋周期为12 s，并保持10 m/s的垂直下降速度。当仿真开始2 s后，机动辨识预测器开始工作，之前状态默认为线性函数，仿真结果如图8所示，图中：函数编号0表示未识别成功，2表示识别为线性函数，3表示识别为二次函数，4表示识别为三角函数。

盘旋机动情况下，机动辨识预测、无预测和线性拟合预测比例导引律的仿真结果见表2。

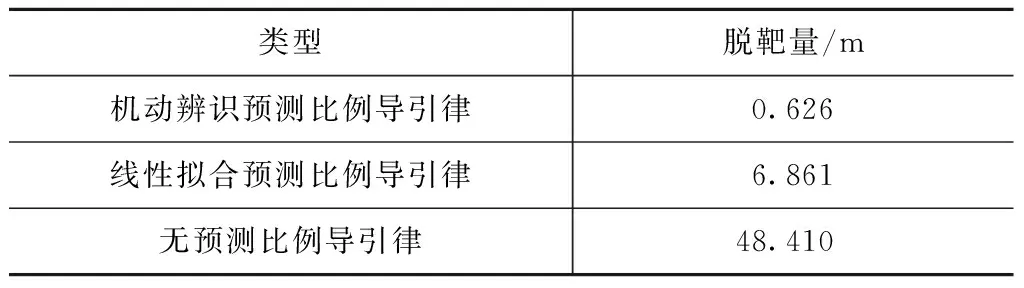
表2 大过载急转机动脱靶量

4.2 大过载滚筒机动

当仿真开始时，目标沿直线匀速巡航，高度角为-5.7°，方向角为185.7°。当仿真时间为10 s时，目标开始进行滚筒机动，过载为19g，滚筒周期为2 s，大过载滚筒机动的仿真结果如图9所示，图中：函数编号0表示未识别成功，2表示识别为线性函数，3表示识别为二次函数，4表示识别为三角函数。

大过载滚筒机动情况下，3种导引律的仿真结果见表3。

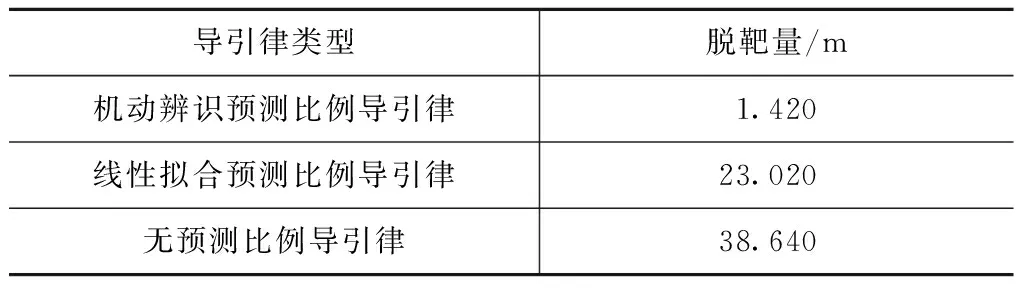
表3 大过载急转机动脱靶量

4.3 大过载复合机动

当仿真开始时，目标沿直线匀速巡航，高度角为-5.7°，方向角为185.7°；当仿真时间为6 s时，目标开始向左盘旋机动，过载为5.5g，周期为12 s；当仿真时间为11.8 s时，目标背对导弹开始进行大过载滚筒机动。仿真结果如图10所示，图中：函数编号0表示未识别成功，2表示识别为线性函数，3表示识别为二次函数，4表示识别为三角函数。

大过载复合机动下，3种导引律的仿真结果见表4。

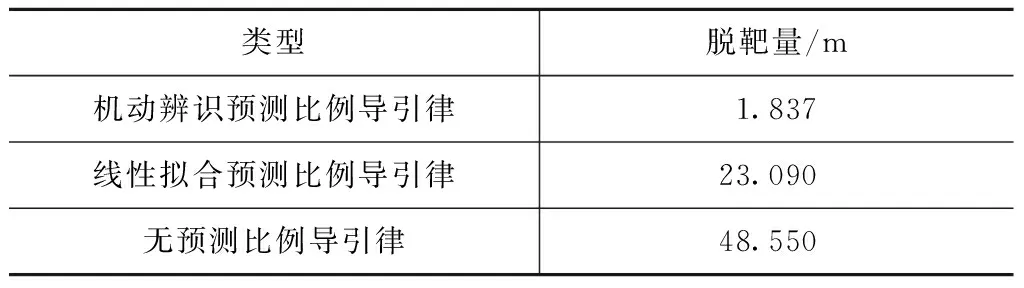
表4 大过载复合机动脱靶量

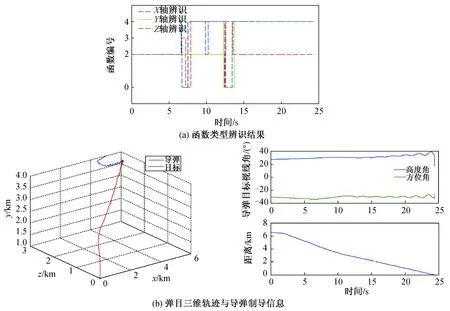
图10 大过载复合机动仿真Fig.10 Simulation of high-g complex maneuver

4.4 算例分析

由仿真结果可见：在有输入干扰的情况下，本文设计的机动辨识预测器在对测量噪声降噪处理后可较准确地辨识目标所处的机动状态。当预测器采样的数据段位横跨2种机动模式时，辨识能力会受到影响。预测器在对盘旋机动辨识时，由于机动周期较长，当采样的数据段位在三角函数平衡点附近时，曲率较低，会被优先识别为线性函数或二次函数，但对预测精度影响较小。

本文所构建的目标机动运动学模型是从目标实际机动类型出发，当目标机动类型是模型库所涵盖的类型时，相对将目标机动描述为随机过程的方法会有更高的预测精度，从而减小导弹脱靶量。对于典型的机动目标，本文方法可将脱靶量控制在2 m以下，而采取其他简单的比例导引律，导弹脱靶量多为几十米。因此，采取无预测比例导引律会把导弹引导至有时间延迟的目标观测点，导致脱靶量很大，仅略小于目标观测点与实际点的距离；采取线性拟合预测导引律则默认目标在时间延迟期间不进行机动，根据最后观测到的信息进行直线补偿，目标机动过载越大，补偿效果越差；而本文提出的机动辨识预测比例导引律对于典型的导弹规避机动具有很高的辨识精度，可准确补偿目标的观测时间延迟。

5 结束语

本文建立了导弹、目标追击三维模型，对现有目标规避导弹的典型机动进行了分析和建模，并建立了配套的运动学模型库，设计了自适应卡尔曼滤波器和包含了采样、辨识、预测环节的目标机动辨识预测器。针对辨识函数特点进行了拟合次序优化，基于比例导引率对不同类型的目标机动进行了仿真试验。结果表明：当目标进行典型规避机动时，可准确辨识出目标机动类型，通过辨识系统给出的参数，可精确补偿导弹导引头获得信息和滤波环节所产生的时间延迟，解决了单一模型适用面较窄、对低过载机动目标预测精度过低的问题。本文方法与其他方法相比，计算量相对较小，预测精度更高，特别在打击高频率、大过载机动目标方面优势明显。当目标采用新的机动类型时，可进一步拓展模型库。但本文在导引策略上采用了较为简单的比例导引律，今后可利用目标辨识预测器所得到的加速度信息设计扩展比例导引律，以提高对目标的追踪性能。此外，在实际情况中，由于导弹舵面具有执行偏差、气流不稳定等缺点，目标的机动轨迹可能无法完全与模型库匹配，对这样的轨迹进行辨识会增加误差，因此应进一步提高本文方法的鲁棒性。