考虑伺服回路动态的飞行器攻角鲁棒控制技术

杨广慧，杜立夫，刘晓东

(北京航天自动控制研究所,北京 100854)

0 引言

日趋复杂的现代战场环境对飞行器，尤其是战术导弹提出了轻质化和高动态的双重要求，然而轻质化的实现会在一定程度上降低伺服的动态特性，造成其姿控回路与伺服回路的频谱分离不够明显。传统的飞行器姿态控制设计方法通常将姿控回路和伺服回路分开设计，并未充分考虑两者之间的交联影响，导致两者之间缺乏有机的协调匹配，无法充分发挥飞行器的最大潜力。此外，为更好地实现制导任务要求，飞行器控制系统会对其伺服系统提出较高的技术指标要求，增加伺服回路的设计难度，因此需要研究考虑伺服回路特性的姿态控制设计方法，从而降低对伺服回路的性能指标要求。为提高飞行器姿控系统的整体性能指标，研究考虑伺服回路动态的姿态控制设计方法极为必要。

对于飞行器这类非线性系统，通常采取多鲁棒面控制与反演设计相结合的方法[1-3]。但是，传统反演方法中的连续微分会带来“计算爆炸”问题。为解决此问题，SWAROOP等[4]提出了一种动态面控制方法。该方法通过引入若干组低通滤波器避免了对虚拟指令的直接微分，具有较高的工程实用价值，得到了国内外学者的广泛关注，并被应用于飞行器的制导控制设计中[5-9]。本文在此基础上，以飞行器俯仰通道为例，借助多鲁棒面控制和动态面控制理论，提出了一种考虑伺服回路动态的攻角控制设计方法。此外，滑模变结构控制方法具有设计简单、鲁棒性强等特点，自首次被提出以来，得到了广泛的研究，并在工程实践中逐渐得到推广和应用[10-11]。因此，在分层设计时，本文将滑模变结构控制理论纳入考虑范围，以提高攻角控制方案的鲁棒性能。为衡量不同控制方案下姿控系统的综合性能，体现本文所提出的控制方案的性能优势，提出了一个用于评价综合性能的指标函数，该函数是关于攻角跟踪误差与控制舵偏量的加权。

1 问题描述

俯仰通道的姿态运动方程组为

(1)

式中：α和θ分别为飞行器攻角和弹道倾角；m和v分别为飞行器质量和速度；g为重力加速度；ωz为俯仰角速率；Jz为转动惯量；q，S和L分别为动压、参考面积和参考长度。气动升力系数CY和俯仰力矩系数Cz的表达式为

(2)

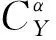
因此，当未考虑伺服回路动态时，面向攻角控制的设计模型为

(3)

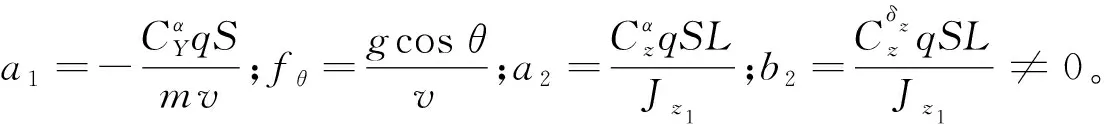
为便于设计，电动伺服回路的动态特性可简化为一个二阶线性环节，即

(4)

式中：ωn为电动伺服系统的自然振荡角频率；ξn为电动伺服系统的阻尼比；δzd为电动伺服系统的输入指令。其中，ωn和ξn的选取需体现伺服回路带宽和动态的设计要求。与式(4)对应的时域表达式为

(5)

因此，当考虑伺服回路动态时，面向攻角控制的设计模型为

(6)

式(3)、(6)建立的数学模型为下一步飞行器攻角控制律的设计奠定了基础。下一节将基于此模型进行攻角控制律的设计。

2 动态面攻角控制律设计

形如式(3)、(6)所示的非线性系统，通常采取反演与多鲁棒面控制相结合的控制方式。但是，传统反演方法中的连续微分会带来“计算爆炸”问题。为避免此现象的发生，可采用动态面控制方法[4]。该方法通过引入若干个低通滤波器避免了对虚拟指令的直接微分，具有较高的工程实用价值。同时，因滑模变结构控制方法设计方便，且具备针对外界干扰和参数摄动的强鲁棒性能，故本文在分层设计时将采用该方法。

针对双层结构的设计模型(3)，即未考虑伺服回路动态时，动态面攻角控制律为

(7)

式中：αd为攻角指令；滤波器系数η>0；k1，q1，k2，q2为控制系数，其值均大于零。

而针对3层结构的设计模型(6)，即考虑伺服回路动态时，动态面攻角控制律则变为

(8)

式中：滤波器系数η1>0，η2>0；控制系数k3>0，q3>0。

下面将重点分析在采用本文所提出的控制算法(8)时攻角控制系统的稳定性。作为分析的前提，首先给出2个具有可行性的假设条件。

假设1系统中的不确定项均是有界的，且满足dα≤κα,dz≤κz,dm≤κm。

假设2当采用动态面控制方法时，低通滤波器的输出信号yfo与输入信号yfi的差值是有界的，且满足yfo-yfi≤κfy。

基于上述2个假设条件，给出本文所提方案下攻角控制系统的稳定性定理。

定理1对于具有3层级联结构的含伺服环节的设计模型(6)，采用动态面攻角控制律(8)，当满足式(9)条件时，飞行器实际攻角α将渐近收敛于指令攻角αd，即攻角控制系统渐近稳定。

(9)

证明采用滑模面变量构建Lyapunov函数

(10)

对Lyapunov函数进行微分计算，得到

(11)

由式(6)、(8)可得

(12)

当采用动态面方法时，有ωzc=ωzd+dfz。因此，式(12)可改写为

(13)

式中：不确定性变量ds1=dα+dfz是有界的，且满足ds1≤κs1=κα+κfz。

然后，将角速度虚拟控制律代入式(13)可得

(14)

同样，由式(6)、(8)可得

(15)

-k3s3-q3sgn(s3)+dm

(16)

(17)

式中：ds2=dz+b2dfm是有界的，且满足ds2≤κs2=κz+b2κfm。

此时，由式(14)、(17)可得

s2-k1s1-q1sgn(s1)+ds1s1+

-k2s2-q2sgn(s2)+ds2s2=

-k1s12-k2s22+s1s2-q1s1+

ds1s1-q2s2+ds2s2≤

κs1s1-q2s2+κs2s2=

q1-κs1s1-q2-κs2s2

(18)

由式(7)、(8)可看出，在未考虑伺服回路动态时，解算出的舵偏角指令为δzd；而在考虑伺服回路动态时，解算出的舵偏角指令变为δzd*。这体现出2种设计方法之间的区别。显然，控制律(8)中包含了伺服回路的动态特性参数。此外，为防止控制量的高频抖动，用如下饱和函数来替代符号函数，即

(19)

可以证明，当采用饱和函数代替符号函数后，若同样满足定理1中的条件，则控制系统的Lypanonov渐近稳定性将退变为有界稳定性。此外，我们可通过调节参数η来减小收敛域界值。实际上，参数η的选取应折中考虑系统收敛精度与控制平滑程度。

至此，在未考虑/考虑伺服回路动态时，即分别考虑双环结构设计模型(3)和三环结构设计模型(6)时，飞行器攻角鲁棒控制律设计完毕。

3 仿真结果

本节将通过计算机仿真，验证本文所提出的控制方案相比于未考虑伺服回路控制方案的性能优势。

仿真中，当未考虑伺服回路动态时，攻角控制律的参数为：k1=20，q1=2，k2=20，q2=2。当考虑伺服回路动态时，攻角控制律的参数为：k1=30，q1=5，k2=30，q2=10，c=500，k3=30，q3=5。 伺服回路的阶跃响应曲线如图1所示。

图1 伺服回路的阶跃响应曲线Fig.1 Step response curve of servo loop

将如图1所示的伺服回路置于飞行器攻角控制系统中，然后比较2种控制方案下的攻角跟踪曲线，如图2所示。由图2可知，当设计中考虑伺服回路动态时，飞行器攻角跟踪的响应速度更快，同时稳态精度更高。

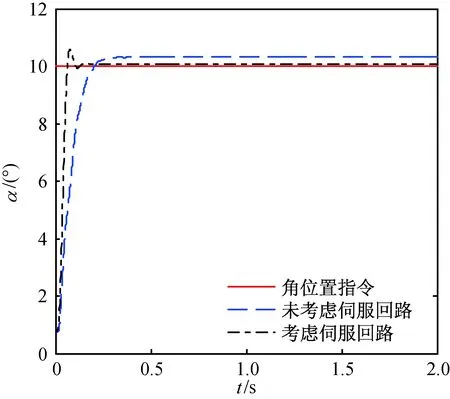
图2 2种控制方案下攻角跟踪曲线Fig.2 Attack angle tracking curves under two control schemes

为更为直观地比较2种控制方案下攻角控制系统的综合性能情况，将性能指标函数定义为

(20)

式中：第1项为跟踪误差相关项，第2项为控制消耗相关项。

2种控制方案下攻角控制系统的性能指标曲线如图3所示。由图3可知，当设计中考虑伺服回路动态时，攻角控制系统的综合性能指标值更小，即具有更优越的综合性能，体现出本文所提出的控制方案的优势。

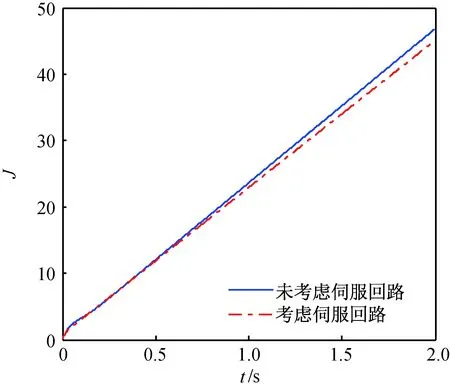
图3 2种控制方案下性能指标曲线Fig.3 Performance index curves under two control schemes

图4 2种控制方案下跟踪误差曲线Fig.4 Tracking error curves under two control schemes

同时，为了体现本文所提出控制方案的鲁棒性，下面将对比未包含鲁棒项的控制方案，其控制律参数为：k1=30，q1=0，k2=30，q2=0，c=500，k3=30，q3=0。于是，2种控制方案下阶跃响应的跟踪误差曲线如图4所示。由图4可以看出，在存在不确定因素的情况下，相比未考虑鲁棒项的控制方案，本文控制方案下攻角跟踪的响应速度更快，稳态精度更高，从而直观体现出其控制性能优势，进而反映出系统鲁棒性能的提升。

4 结论

为提高姿控外回路和伺服内回路的协调匹配性，本文提出了一种考虑伺服回路动态的攻角鲁棒控制设计方法。采用滑模控制与动态面控制相结合的方法，实现了对象3层子系统之间的有效级联。计算机仿真结果表明：相比于未考虑伺服回路动态的姿控设计方法，本文所提出的控制方案具有更好的攻角跟踪效果和更优越的综合性能指标，包括跟踪误差和控制能量消耗。该控制方案结构清晰，便于工程实现，可重点应用于具有高动态和轻质化要求的飞行器姿态控制领域，并可推广应用于飞行器全通道姿态控制。