水平悬链线中点集中力作用下的非线性分析及计算
, , ,
(1.湘潭大学 土木工程与力学学院,湘潭 411105;2.长沙矿冶研究院 深海矿产资源开发利用技术国家重点实验室,长沙 410012)
1 引 言
悬链线数学解在工程领域应用广泛,魏建东等[1]采用两节点悬链线单元,以确定连续滑移索的平衡位置。杜敬利等[2]采用基于悬链线的柔索静力学模型定位机械人的静态平衡位置,但对于初始平衡态增量过渡到最终平衡态的路径依赖未予详细说明。文献[3-5]分别从不同的角度探讨了悬链线理论在相关工程领域的应用。杨孟刚等[6]采用两节点悬链线索元对集中力作用下的柔索结构进行了非线性有限元分析计算。秦剑等[7]基于悬链线理论对分段悬索结构进行找形计算,但找形计算中的初始构型采用抛物线逼近,故找形结果只适宜于小垂度的情形。康庄等[8]采用悬链线和大变形梁理论建立了模拟J型铺设管线的分段力学模型。毛东风等[9]采用大扰度梁理论、Pasternak地基模型和悬链线理论,借助ABAQUS模拟了深水管道弃置回收过程的力学行为,属于典型的工程应用。张卓杰等[10]在悬链线的求解中,选取左边界的斜率即广义倾角α的映射作为初始试探值,反复迭算求得悬链线的解答,但计算过程过于迂回。冯海暴[11]采用悬链线理论对35 m作业水深的铺排管线进行了力学分析,但采用的方程要求广义倾角α=0,很难适用于流体动力的变化。黄新波等[12]利用Ansys软件进行了索结构的找形分析,表明有限元软件的找形分析结果可以与悬链线理论相匹配。
综上,学者对于悬链线进行了一系列研究[3-5,13-15],体现了悬链线解的广泛应用价值,也表明悬链线的理论求解有待完善。关于悬链线任意位置作用集中载荷的力学行为,概念上可采用脉冲函数[13]来建立相关的数学方程进行分析。目前对于集中力作用下悬链线的力学数学行为研究较少。
左右两端的垂直坐标不相等,两端点的连线是一条倾斜直线。悬链线左右两端的垂直坐标相等,两端点的连线是一条水平直线,该边界约束情况称为两端水平约束,此时均布对称载荷作用下悬链线具有对称性;在两端水平悬链线中点作用垂向集中力,悬链线分析便具有了双重对称性,即水平几何约束的对称性和力作用位置的对称性。在双重对称性下悬链线的分析是几何约束不对称与集中力作用位置不对称一般问题分析的特异,其解可以说是悬链线非对称性情形下非线性超越方程的特殊解或奇异解。
2 分布力作用下单索悬链线理论
分布力作用下单索悬链线的理论是集中力与分布力同时作用的基础。该理论采用两个前提[14],一是悬链线仅承受张拉,任意截面不具备抗弯能力,即抗弯能力可假设为0;二是悬链线受作用力时长度保持不变,即悬链线不可拉伸。
对于仅受垂向集中力作用下的结构,其任意截面水平方向合力处处相等。柔索在均布垂直荷载q作用下任意挠度的悬链线解为[14]
(1)
式中h为沿悬链线不变的水平张力,α为左边界a处斜率的广义倾角,边界处a的斜率为shα;xa和ya分别为悬链线左端点a处的横坐标和纵坐标,sh为双曲正弦函数,ch为双曲余弦函数。线均布载荷q的单位为N/m,张力的单位为N。
悬链线右端点b处的坐标为[xb,yb]。令l=xb-xa,表示悬链线左右两端的相对水平距离(简称水平距离),c=yb-ya表示悬链线左右两端的相对垂直距离(简称垂直距离)。y轴向上为正,x轴向右为正。
式(1)中高度绑定的表达式h/q具有本质含义,表示悬链线内在的曲率半径r,因而定义曲率半径r或曲率直径D为
r=h/q,D=2r=2h/q
(2)
曲率半径r是悬链线至关重要的参数,形式上表示单位线均布载荷产生的水平张力。悬链线在水平距离l变动时存在一个不能逾越的极限水平距离d(简称极限距离),计算式为
(3)
极限距离d对应的线是一条直线,是悬链线的水平距离l无限逼近d时悬链线的渐近线,简称极限渐近线。
定义无量纲参数b为
(4)
无量纲参数b的倒数等于水平距离l与水平极限距离d之比,为位于区间(0,1)的正小数。无量纲参数b越小,曲率半径r越大,且b无限接近于1时,曲率半径r趋于无穷大,悬链线越逼近悬链线的极限渐近线即越逼近直线;无量纲参数b越大,曲率半径r越小,且水平距离l越接近于0,曲率半径r趋于0。
定义无量纲参数β为
(5)
无量纲参数β正比于曲率,β越大,悬链线弯曲得越厉害,水平张力越小。无量纲参数β的倒数z=D/l=2h/ql正比于单位均布载荷单位水平距离对应的水平张力,可称为相对水平张力。
不失一般性,将坐标系放置于左端点a处,利用式(1,2),可得从起点到任意位置x处的索长度为
(6)
定义广义倾角θ为
θ=α+β
(7)
根据双曲正弦、双曲余弦函数和差化积公式以及式(2,5),悬链线y坐标和索长度的计算公式可以写为
y(x)=Dsh(x/D+α)shβ
(8)
s(x)=Dch(x/D+α)shβ
(9)
利用边界约束条件c=y(l)和s=s(l)与式(5,7),由式(8,9)可知,广义倾角θ的计算式为
(10)
广义倾角θ与水平距离l无直接关系,是c和s之比的反双曲正切函数。当水平距离l趋于水平极限距离d时,广义倾角θ趋于α。根据双曲函数的性质和式(10),广义倾角θ存在以下关系式,
(11)
式(11)可视为悬链线在极限距离斜率的几何映射关系。其中th为双曲正切函数,cth为双曲余切函数。将式(5,10)引入式(7)得到广义倾角α的计算公式为
将边界约束条件c=y(l)和s=s(l)分别代入式(8,9),并利用表达式(2,5),经运算简化得到隐含水平张力的非线性超越方程为
(12)
式(12)是本质一致表达方式不同的方程,表示悬链线总体的刚性平衡关系。根据方程sh(l/D)=d/D可求出悬链线曲率直径D=2r依赖于双参数l和d的离散数值关系。而从方程sh(β)=bβ可求出广义倾角β与b=d/l的单参数依赖关系。无论是单参还是双参依赖关系,在l 根据双曲函数的性质和式(5,12),关于无量纲参数β存在关系式: (13) 式(13)可视为悬链线段两点边界约束的静力平衡关系,其中p的计算公式为 (14) 即p2=d2+D2,而极限距离d是水平距离l的上限,曲率直径D是特定悬链线所有曲率直径的下限,两者是悬链线潜在的特征量。 索中张力的垂直分量V[14] 为 V=h(dy/dx)=hsh[(α+(q/h)(x-xa)] (15) 双曲正弦函数shx可正可负,从而垂直分量V也可正可负。式(15)索中张力的垂直分量V是左区域索右边界上的受力,是沿弧长方向张力T的y向投影,斜率向下时其值为负,斜率向上时其值为正。 利用式(11~15)以及双曲正弦、双曲余弦的和差展开公式,在左端边界x=xa处的约束反力垂直分量Va和在右端边界x=xb处的约束反力垂直分量Vb可写为 (16) 式(16)避免了复杂的双曲函数,便于悬链线理论的深入应用。 悬链线最低点[xmin,ymin]是悬链线斜率为0的点,该点张力T最小,张力T的垂直分量V=0,根据式(15),xmin位置关于xa的偏移x0=xmin-xa为 (17) 利用式(1,11~13,17),可得悬链线最低点到两端点较小值的距离f为 (18) 对于两端水平悬链线,c=0时,d=s,从式(18)可得到悬链线的垂度f,悬链线最低点位于区间的中点。 (19) 若令悬链线的弧长为2s,式(19)的垂度f改为垂直距离c,则从式(19)可以反解出水平张力关于弧长s和垂度c的显式表达为 hc=(q/2)(s2-c2)/c (20) 式(20)也可以从临界边界条件广义倾角α=0和方程(7,12)导出,表示悬链线临界情形下,两点边值问题水平张力h的显式解答。 水平悬链线是悬链线左右两端连线为水平直线的悬链线,在其整个索长的中点作用垂直方向的集中力。不失一般性,本文考虑垂向集中力向下的情形。这是一个双重对称性问题,即几何约束对称和集中力作用位置对称。 根据对称性可将水平悬链线分解为两个左右对称的悬链线进行分段处理,集中力作用点作为特殊点,一方面用于保持左右两边悬链线函数点的连续,另一方面分离出提供力的平衡方程。 为公式简洁起见,令原水平悬链线中点向下作用的垂向集中力为2W。取右边悬链线为研究对象。根据对称性,2W垂向集中力分配给左右两边悬链线相邻端点各1W的集中力。右边悬链线的相对水平距离为l,索长为s;整个悬链线的索长为2s,水平距离为2l。水平距离l在双重对称性问题中是保持不变的已知量,索长s原本对应未加集中力时整个悬链线的中点,也是已知量。如图1所示。 在垂向集中力的作用下,右边悬链线左端点即集中力作用点在水平距离l界定的垂直直线上移动,最终平衡于相对垂直距离c,c是一个待求的变量。右边悬链线右端点以及左边悬链线左端点保持为约束状态。 整个悬链线仅受垂直方向的外力作用,因此左右两段悬链线中的水平张力处处相等,以h表示,是一个待求的变量。当在右悬链线的左端点作用向下的垂向集中力W时,左端点的受力分析如 图1 所示。在右悬链线上,因为斜率大于等于0即shα≥0,所以有右悬链线在左端边界处的垂直分量Va≥0,等号仅在W=0时成立。根据力学平衡有 图1 悬链线的受力示意图 Fig.1 Force diagram of the catenary Va=W (21) 方程(21)本质上为力边界约束条件,将悬链线左端边界处的约束反力垂直分量关系式(16)代入式(21)可得 (22) 从式(22)可见,集中力W与分布力q绑定在一起,因而定义具有长度量纲的参数w为 w=W/q (23) 参数w为向下垂向集中力W与悬链线的分布力q之比,即w=W/q。w可称为集中力均布化处理后的折算长度。定义简化表达式的参数u为 u=2W/q+s=2w+s (24) 综合式(22~24),考虑到式(2)即h=Dq/2,原水平悬链线中点向下作用2W垂向集中力时,左右两段悬链线新平衡构型对应的水平张力h为 (25) 将方程(25)代入悬链线段平衡方程(12)即sh(l/D)=d/D,可以得到左右两段悬链线新平衡构型对应的相对垂直距离c,应满足下面的超越方程, (26) 方程(26)是数学上混合边界问题的解,在双重对称性条件下作用分布力与集中力时,方程(26)就是求解未知平衡构型点c的非线性数学平衡方程。 当垂向集中力W=0时,方程(25)回归到方程(20),方程(26)回归到方程(12)。 值得指出,在上述相关方程中,取索长s=1与均布力q=1,可得到相应的无量纲方程以及相关的无量纲量。本文采用收敛性较好的二分法来求解无量纲方程中的待求量c/s。当无量纲水平距离即l/s<0.000007且无量纲集中力W/qs>100时,二分法求根算法尚未无条件收敛。物理上水平距离l趋于0时,垂直距离c趋于s,此时方程(26)的l/d处于0/0的状态。因此本文采用的无量纲水平距离l/s介于[0.0001,0.999999]。当集中力W=0时,左右分段悬链线的合并便是整段导数光滑的原始悬链线。 图2所示为当右悬链线垂向集中力W介于0~4.5qs且l介于0.1s~0.9s时,不同垂向集中力作用下水平张力的变化趋势。水平距离l取特定值0.8s时的连线接近直线,实际上图中每一条连线都是一条曲率很小的曲线,水平张力h随垂向集中力W增大而增大,但不是线性的正比关系。水平距离l越大,相应的水平张力h也越大。 图3表示初始垂度f、平衡垂直距离c和极限垂直距离ck随水平距离l的变化关系及相应的计算公式。分图①示意偏大的水平距离l,分图②示意中等的水平距离l,分图③示意偏小的水平距离l。随水平距离l增大,初始垂度f、垂直距离c和极限垂直距离ck减小。在相同水平距离l下,集中力W减小,垂直距离c减小;集中力W增大,垂直距离c增大。(c-f)/s的最小值位于计算域的左右两端点,或在计算域的左边端点或右边端点,这取决于集中力的大小和左右两端点本身的大小。 图2 不同垂向集中力作用下水平张力的变化情况 Fig.2 Variation of horizontal tension under the effect of different downward point forces 图3 初始、平衡和极限垂直距离随水平距离的变化 Fig.3 Variation of initial,balance and limit vertical distance with horizontal distance 概念上无量纲水平距离l/s趋于1或趋于0,(c-f)/s皆趋于0。Max.(c-f)/s表示集中力W作用下无量纲因变量l/s跑遍计算域[0.0001,0.999999]时(c-f)/s的最大值,简称为最大垂直距离差。对于特定的W/qs,(c-f)/s的极值点位于l/s该计算域的内部某点,且极值点即最大值点是唯一的。当W/qs=0.0001时,Max.(c-f)/s位于l/s=0.01处;当W/qs=0.02时,Max.(c-f)/s位于l/s=0.24处;当W/qs=0.2时,Max.(c-f)/s位于l/s=0.52处;当W/qs>200时,Max.(c-f)/s趋于l/s=0.656283。垂直距离差(c-f)/s关于l的变化是中间大两端小非对称上凸单峰曲线,Max.(c-f)/s最大值所在水平位置l随集中力W增大而增大,最终趋于l/s=0.656283,此时Max.(c-f)/s=0.0752059。结果如图4和图5所示。 图6所示为当右悬链线垂向集中力W介于0~4.5qs且l介于0.1s~0.9s时,悬链线两点的垂直距离差c-f发生改变的趋势。随着垂向集中力W增大,垂直距离差c-f相应增大。当垂向集中力W>1.5qs时,垂直距离差c-f变化减弱,几乎接近于水平直线。当垂向集中力W<1qs时,垂直距离差c-f变化剧烈。当l/s介于0.5~0.75之间且W>1.5qs,垂直距离差c-f偏于较大值,约介于0.065s~0.0752s。注意,l/s=0.9 对应的(c-f)/s曲线段在W>0.5qs时,低于l/s=0.4,0.8,0.5,0,6和0.7对应的(c-f)/s曲线段。计算和分析结果表明,无量纲水平距离l/s趋于1时,(c-f)/s趋于0。 图4 最大垂直距离差所在水平位置随集中力的变化 Fig.4 Variation of horizontal location and maximum of vertical distance difference with concentrating forces 图5 垂直距离差关于水平位置随不同集中力的变化 Fig.5 Variation of vertical distance difference along horizontal location with different concentrating forces 图6 垂向集中力作用下垂直距离差的变化 Fig.6 Variation of vertical distance difference under the vertical concentrating forces (1) 引入两点位移边值约束方程,得到求解悬链线水平张力的超越方程。在数值计算上确定了单参数形式和双参数形式超越方程数值解的一致性。 (2) 给出了悬链线在上下边界的垂直约束反力与曲率半径r及几何参数l,s和c的函数关系。这种简单函数关系便于数学上解决或处理悬链线放松约束时的逆问题。 (3) 推导出既有均布力又有集中力作用在悬链线对称位置时应满足的平衡方程,得出分段悬链线依赖于集中力的函数关系。探讨了当集中力等于0时,分段方程向原整段悬链线方程的和谐回归,证明本文理论构建数学逻辑的自洽性。 (4) 通过无量纲处理,计算了在不同集中力作用下不同水平距离悬链线的复杂力学响应,其中最大垂直距离差的非对称和非线性行为特别值得关注。 本文建立的水平悬链线中点集中力作用下的数学模型是更复杂非对称性问题的特例,可作为一般性非对称性问题的导引。3 悬链线上下边界的约束反力
4 悬链线最低点的坐标与水平张力的显式解
5 集中力作用水平悬链线对称性位置的力学特性
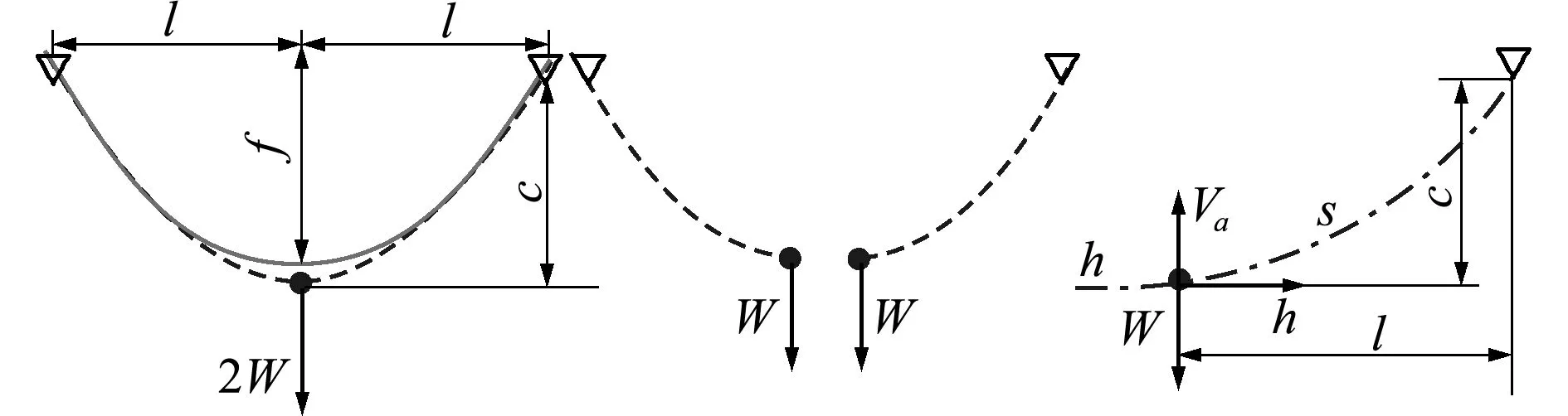

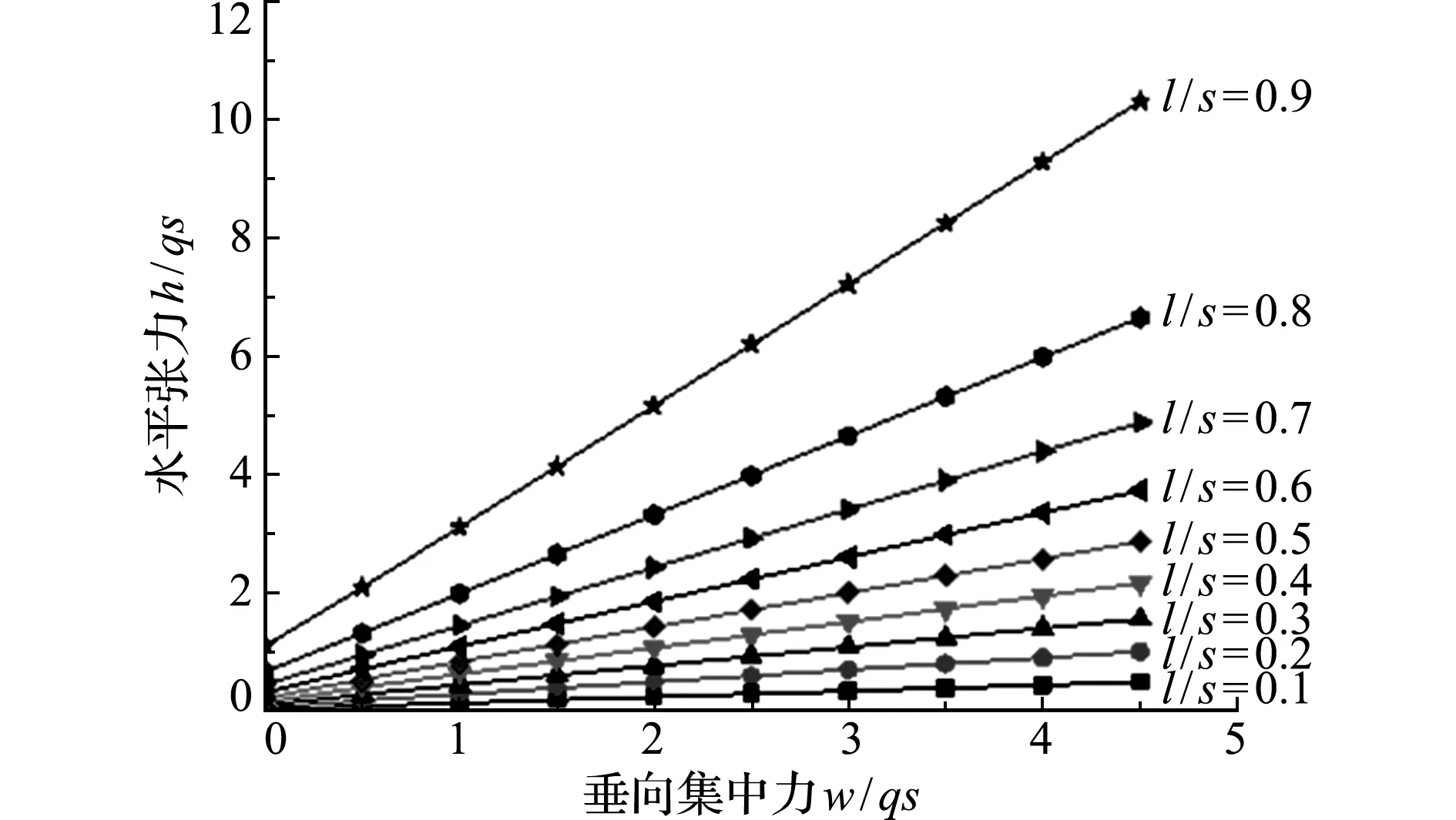
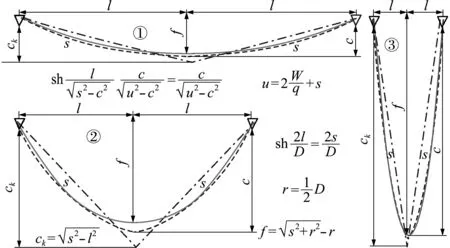


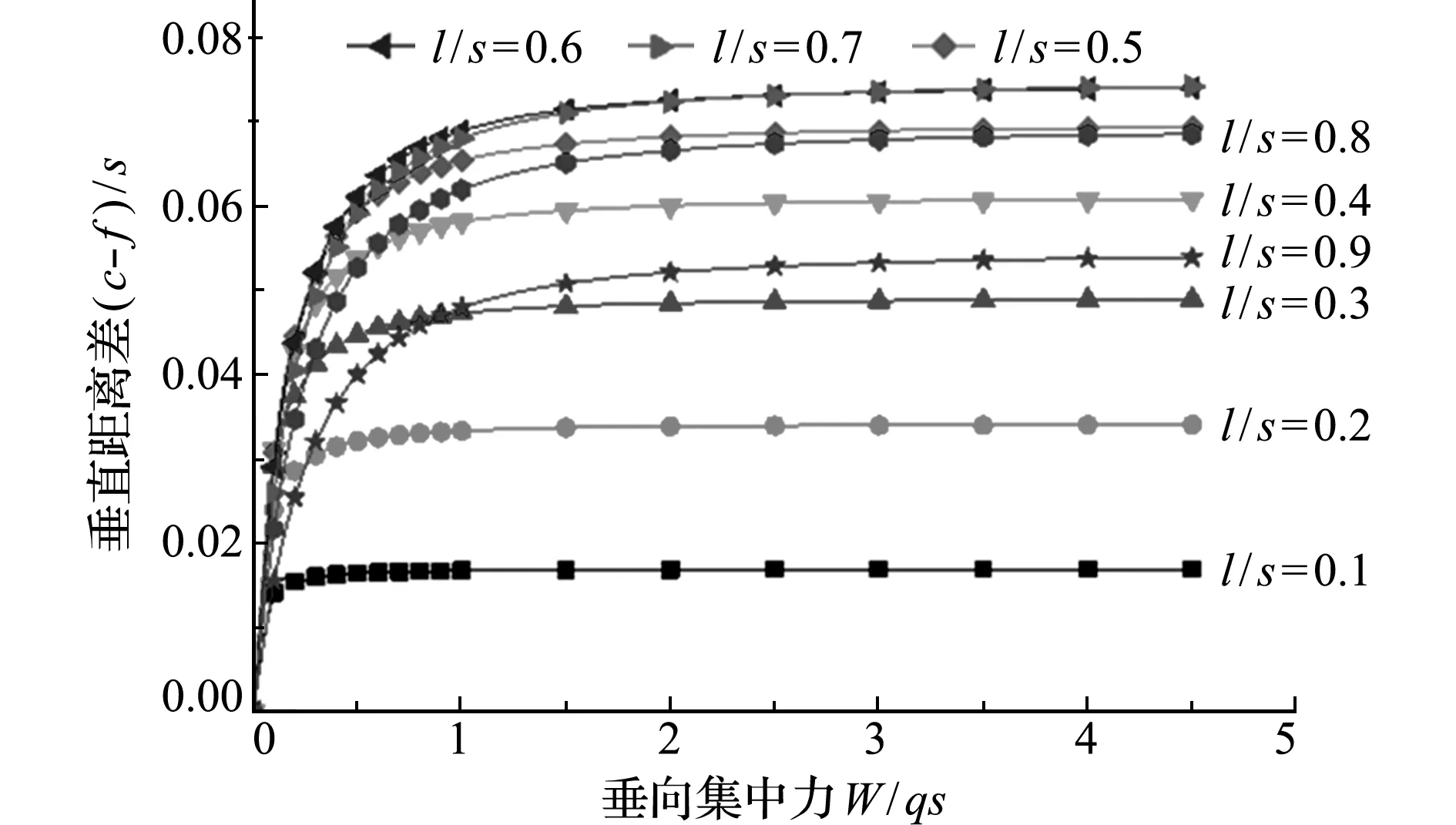
6 结 论
——超集中力
—— 梁在集中力作用点处的剪力分析

