基于Armijo准则的自适应稳定转换法

，

(大连理工大学 工程力学系 工业装备结构分析国家重点实验室，大连 116024)

1 引 言

在实际工程应用中，制造和测量引起的不确定性无处不在，包括材料不确定性、载荷不确定性和几何不确定性，而结构可靠度分析方法[1-8]是处理不确定性问题，保证结构设计安全的有效工具。一次二阶矩法FORM(First Order Reliability Method)在工程界应用广泛，具有概念清晰、求解简单和计算效率高的优点。FORM的主要思想是将结构失效概率的计算转化为求解失效域内联合概率密度最大的点，简称为最可能失效点MPP(Most Probable failure Point)，该点的几何意义是标准正态空间内极限状态面上离原点最近的点，因此FORM的本质是非线性约束优化问题。

HL-RF算法[9,10]是求解MPP的一种常用梯度类迭代方法，计算效率高，但对于高非线性问题会出现周期解或混沌解等。为了改善HL-RF算法的稳定性，近几年出现了多种改进方法。Liu等[11]将merit函数引入HL-RF算法中，提出MHL-RF算法，用于克服HL-RF算法迭代过程不收敛的问题。Lee等[12]引入一个检测之字型振荡的判据，对迭代式进行改进，达到了减小振荡的目的。Santosh等[13]引入与MHL-RF算法相同的merit函数，且结合Armijo准则对MHL-RF算法进行改进。Zhang等[14]引入一个不可微merit函数，并结合Armijo准则提出了改进的HL-RF(iHL-RF)算法。Keshtegar[15]将混沌动力学的稳定转换法与共轭梯度搜索方法结合，提出了混沌共轭稳定转换法CCSTM(Chaotic Conjugate Stability Transformation Method)，可以有效地改善HL-RF的收敛性，且具有较高的计算效率。杨迪雄等[16]通过混沌动力学分析了一次二阶矩法的数值不稳定性机理，并基于混沌控制理论的稳定转换法STM(Stability Transformation Method)提出了改善一次二阶矩方法收敛性的混沌控制CC(Chaos Control)算法[6,17]。贡金鑫等[18]通过引入一种步长参数，提出了有限步长FSL(Finite-Step Length)算法，实现了收敛性的改善。孟增等[19]针对HL-RF迭代过程振荡具有方向性的特点，对CC算法进行修正，提出了方向性稳定转换法DSTM(Directional Stability Transformation Method)，不仅收敛性得到改善，而且计算效率比CC算法更高。在求解中等或高度非线性问题时，上述各类改进方法都是通过减小步长(或控制因子)来提高迭代过程的数值稳定性，而减小步长(或控制因子)会导致计算量增加，因此对FORM而言，一个稳定的迭代方法不仅需要具备搜索MPP的准确性，而且需要尽量减小计算量。

本文将Armijo准则与DSTM算法进行结合，提出了基于Armijo准则的自适应稳定转换法AASTM(Armijo -based Adaptive Stability Transformation Method)算法。本文算法采纳了DSTM算法的方向性混沌控制策略，而控制因子的大小通过Armijo准则进行自适应调整，使算法既保证了迭代收敛，又提高了计算效率。

2 Armijo准则

Armijo准则是求解无约束优化问题的一种非精确一维搜索准则，最早由Armijo等[20,21]提出,该准则的目的是保证优化算法能够收敛至最小值。

设有一个无约束最小值优化问题，可表示为

min.f(u) (u∈Rn)

(1)

式中Rn为n维欧氏空间。采用梯度类迭代算法求解该优化问题时,通常采用迭代式:

uk +1=uk+αkdk

(2)

式中αk为第k个迭代步的步长，dk表示下降方向，与目标函数的负梯度有关。

在求解非线性优化问题时，通常采用非精确一维搜索，如基于Armijo准则的一维搜索。Armijo准则的主要思想是在uk点确定了下降方向dk后，只需由式(2)得到下一个迭代点uk +1，然后使目标函数值满足一定的下降，而下降量需要满足不等式关系：

f(uk +1)≤f(uk)+ραk(gk)Tdk

(3)

式中gk=f(uk)为目标函数f在迭代点uk处的梯度向量；ρ为常数，且满足ρ∈(0,0.5)。

对于FORM，计算MPP和可靠度指标β需要求解优化问题：

s.t.G(u)=0

(4)

式中u=T(x)为随机变量x在标准正态空间内的映射，通常需要由物理随机空间变换到标准正态空间；G(u)为极限状态函数。该优化问题的最优解u*即为MPP，可靠度指标为β=‖u*‖。

Zhang等[14]提出的iHL-RF算法采用Armijo准则，且将不可微merit函数(5)作为目标函数。

(5)

式中c=2‖u‖/‖G(u)‖。由此，式(4)可转化为如式(1)所示的无约束优化问题，基于Armijo准则求解该优化问题，采用式(2)进行迭代，每一个迭代步的步长αk需满足式(3)，而式(3)中目标函数的梯度gk和下降方向dk可分别表示为

gk=f(uk)=uk+ck·sign[G(uk)]G(uk)

(6)

(7)

通过Armijo准则，iHL-RF算法实现了自适应调整每个迭代步的步长，可以有效减小振荡次数，保证迭代收敛性。但同时为了获得自适应步长，需要提供额外的计算量，且振荡的控制过程未考虑振荡具有方向性的特点，由此会导致迭代步增加。

3 方向性稳定转换法

3.1 振荡的方向性

采用HL-RF算法搜索MPP的迭代历程主要分为收敛、振荡收敛和不收敛三种类型[22],如图1所示。图1(a)连续三个迭代点的连线构成的夹角都是钝角，且相邻迭代点距离越来越小，这种迭代历程属于收敛。图1(b,c)连续三个迭代点的连线构成的夹角会出现锐角的情况，但图1(b)的振幅随着迭代逐渐减小，且相邻迭代点距离也越来越小，这种迭代历程属于振荡收敛；而图1(c)的振幅及相邻迭代点的距离会逐渐增大，这种迭代历程属于不收敛。

在标准正态空间内，通常选取原点作为初始迭代点u0。在原点与迭代点连线的垂直方向上，如果连续两个迭代步出现迭代点迂回现象，则可判定此时发生了迭代振荡，同时可以认为原点与迭代点连线的垂直方向是迭代振荡的主方向，减小该方向上的振幅可以实现对迭代振荡的控制。

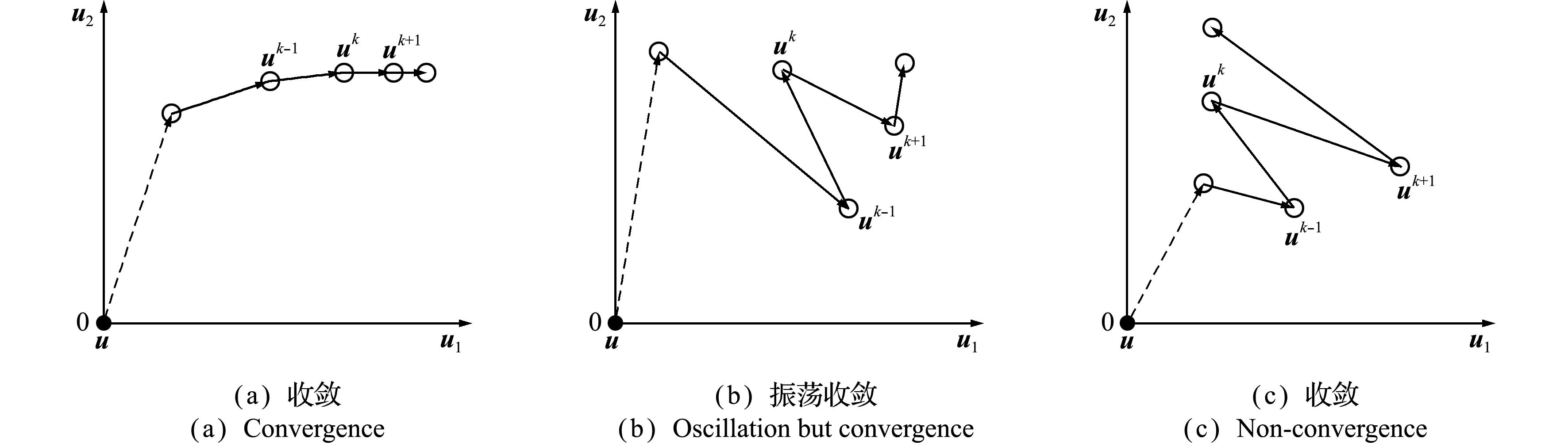
图1 迭代历程的三种类型

Fig.1 Three types of iteration history

3.2 方向性稳定转换法

稳定转换法是混沌动力学控制理论中对混沌运动轨迹进行有效控制的一种方法，杨迪雄[6,17]基于此方法对HL-RF的收敛性进行改进，提出了CC算法，引入混沌控制因子对迭代振荡进行控制：

uk +1=uk+λC[F(uk)-uk]

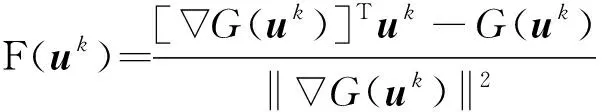
(8)

式中λ为一个0～1的常数，表示混沌控制因子，C为一个n×n维对合矩阵，一般取为单位矩阵。

比较式(2，8)可以看出，iHL-RF算法采用变步长，而CC算法采用固定混沌控制因子。除此之外，两者的迭代式在形式上几乎一致，且采用相似的振荡控制机理，即减小步长或混沌控制因子，从而实现振幅和迭代步同时减小。由于两者都未考虑振荡的方向性，迭代收敛后的计算量会较大。

对于上述情况，孟增等[19]提出了方向性稳定转换法DSTM，在振荡的主方向上进行混沌控制，而在原点与迭代点连线方向上进行放松，其迭代式为

(9)

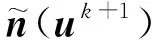
βk +1={G(uk)-[G(uk)]Tuk}/‖G(uk)‖

(10)

DSTM的混沌控制考虑了振荡的方向性，不仅可以使迭代方向得到有效的振荡控制，还能保证迭代步长不至于过小，从而提高计算效率。但是，DSTM中的混沌控制因子依然是一个预先给定的常数。当给定的控制因子过大时，DSTM可能迭代不收敛；当给定的控制因子过小时，可能使迭代收敛需要很大的计算量。因此，如果能自适应调整混沌控制因子，算法的计算效率和鲁棒性就能同时得到保证。

4 基于Armijo准则的自适应稳定转换法

4.1 混沌控制因子的自适应调整策略

由于Armijo准则可以自适应调整步长保证收敛，而方向性稳定转换法有助于提高计算效率，因此本文将两者结合，提出基于Armijo准则的自适应稳定转换法AASTM，通过Armijo准则对方向性稳定转换法的混沌控制因子进行自适应调整，采用迭代式：

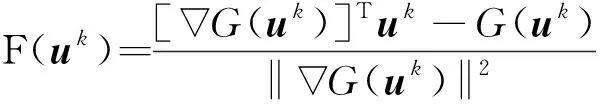
(11)

式中 混沌控制因子λk根据Armijo准则自适应选取，迭代点uk和uk +1需要满足关系：

f(uk +1)≤f(uk)+ρλk(gk)Tdk

(12)

式中ρ为0～0.5的常数，f(·),gk和dk的表达式分别对应式(5～7)。

在选取λk时，Armijo准则采用

λk=0.5m(m=0,1,2,3,…)

(13)

式中m为非负整数，从0依次递增选取，且随着m值递增，对应的λk值会逐渐减半，而式(12)的不等式关系也会由不满足逐渐变为满足。

当λk值减小至第一次满足式(12)时，选取当前的λk值作为方向性稳定转换法的混沌控制因子，代入式(11)求得下一个迭代点，此时表示通过方向性稳定转换法可以实现对迭代振荡的主动控制。

当λk值无论怎样减小，式(12)都不能得到满足时，表示通过方向性稳定转换法对迭代振荡的控制失效，而采用放松的可靠度指标迭代式(10)会加剧振荡。因此，对于这类情况，需要对λk设置下界值λL。当λk≤λL时，将λk值取为λL并作为混沌控制法的控制因子，代入式(8)求得下一个迭代点。本文设定λL=0.05。

4.2 算法流程

图2为基于Armijo准则的自适应稳定转换法的流程，具体步骤如下。

(1) 令k=0，选择随机变量的均值x0作为迭代初始点。

(2) 通过JC法或Rosenblatt变换，将非正态随机变量xk变换为标准正态空间(U空间)内的随机变量uk，且令每步的混沌控制因子初始值为λk=1。 (3) 判断λk值是否低于下界值λL，如果λk>λL，则转至步骤(4)；否则将λk值取为λL，并代入式(8)求得下一步迭代点uk +1，然后转至步骤(5)。

(4) 由式(12)判定当前迭代步是否需要减小混沌控制因子，如果式(12)不满足，采用式(13)对λk值减半，然后返回步骤(3)；否则输出λk值并代入式(11)，求得下一步迭代点uk +1。

(5) 将随机变量uk +1从标准正态空间转换至原物理随机空间(X空间)，得到xk +1。

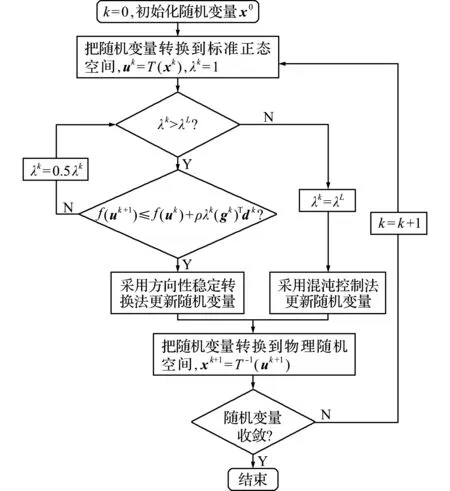
图2 基于Armijo准则的自适应稳定转换法的流程

Fig.2 Flowchart of the Armijo -based adaptive stability transformation method

(6) 计算前后两个迭代点之间的相对变化是否满足不等式‖xk +1-xk‖/‖xk +1‖≤ε，ε为规定的允许误差。如果满足，则停止迭代，否则转至步骤(2)。

5 算例分析

基于四个非线性算例，将本文提出的AASTM算法和其他四种算法(包括HL-RF，iHL-RF，CC和DSTM)进行性能比较。迭代初始点取随机变量的均值，对应标准正态空间内的原点；各算法的停止准则为‖xk +1-xk‖/‖xk +1‖≤10-4。

5.1 二维非线性数值算例

式(14)是一个含二次多项式的非线性极限状态函数[23]，该函数含有两个独立的随机变量x1和x2，均服从标准正态分布。

g=x1-1.7x2+α(x1+1.7x2)2+5

(14)

式中 参数α为二次项的系数，控制该极限状态函数的非线性程度，α值越大，函数的非线性程度越高，取α=1.5。采用HL-RF，iHL-RF，CC，DSTM和AASTM五种算法分析该算例，其中CC和DSTM的混沌控制因子设为0.05。

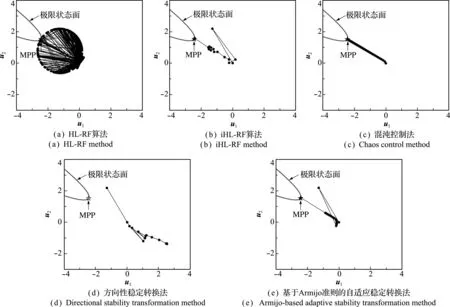
图3 不同方法下算例1的MPP搜索路径

Fig.3 MPP search paths of different methods for example 1

图3中u1和u2分别对应随机变量x1和x2在标准正态空间(U空间)中的映射值，即在U空间内呈现算例1关于不同算法的MPP搜索路径。从图3(a)可以看出，采用HL-RF算法搜索MPP会发生严重的迭代振荡，且迭代至最后仍不收敛。从图3(d)可以看出，DSTM搜索路径虽然收敛，但收敛结果不在极限状态面上，表明此时DSTM未能求得MPP。从图3(b,c,e)可以看出，iHL-RF、CC和AASTM三种算法均能最终搜索至MPP。

各算法最终搜索的结果列入表1，通过函数计算次数比较各算法的计算效率(除了iHL-RF和AASTM迭代过程为了自适应调整步长大小或控制因子需要额外计算极限状态函数，其他算法的函数计算次数=迭代次数×(N+1)，N为随机变量数)。由表1可以看出，虽然DSTM的函数计算次数最少，但由于收敛时g(x*)=9.9≫0，即收敛失效，DSTM的计算效率不参与比较。iHL-RF、CC和AASTM三种算法可以得到基本一致的收敛结果，对应准确的MPP，且三种算法中AASTM的计算效率最高。

5.2 两自由度动力学系统算例

图4是一个两自由度系统[24]，该系统含有主次两个结构。该算例是面向次结构的可靠度分析，而次结构的极限状态函数与系统属性密切相关，如式(15)所示：

(15)

表1 算例1计算结果

Tab.1 Results for example 1

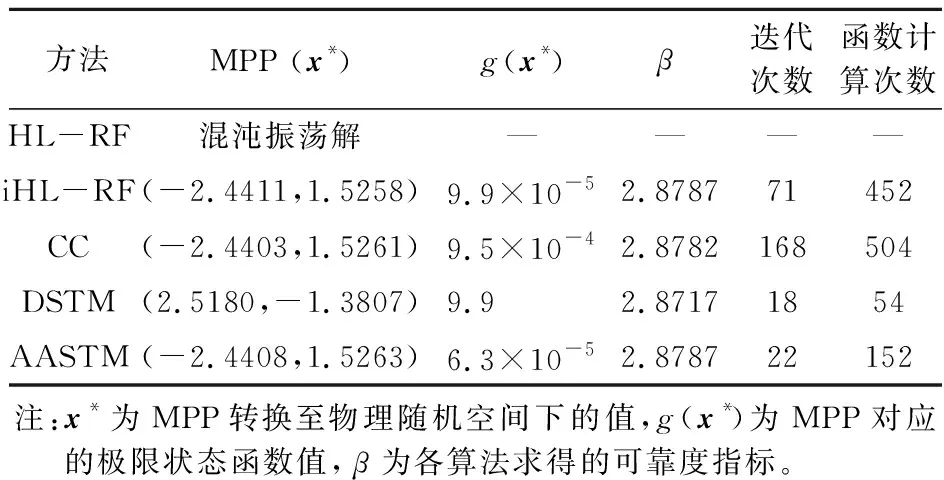
方法MPP (x*)g(x*)β迭代次数函数计算次数HL-RF混沌振荡解————iHL-RF(-2.4411,1.5258)9.9×10-52.878771452CC(-2.4403,1.5261)9.5×10-42.8782168504DSTM(2.5180,-1.3807)9.92.87171854AASTM(-2.4408,1.5263)6.3×10-52.878722152注:x*为MPP转换至物理随机空间下的值,g(x*)为MPP对应的极限状态函数值,β为各算法求得的可靠度指标。

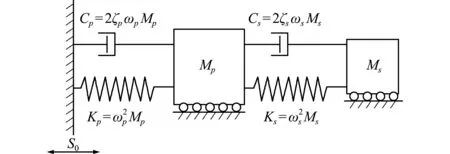
图4 含主次结构的两自由度动力学系统

Fig.4 Two -degree -of-freedom primary-secondary dynamic system

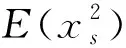
(16)

式中S0为白噪声强度；γ=Ms/Mp为质量比，Mp和Ms分别为主次结构的质量；ωa=(ωp+ωs)/2为平均频率，ωp和ωs分别为主次结构的自振频率；ζa=(ζp+ζs)/2为两自由度系统的平均阻尼比，ζp和ζs分别为主次结构的阻尼比；θ=(ωp-ωs)/ωa为系统的调谐参数。该算例包含8个服从对数正态分布的随机变量，其分布参数列入表2。采用五种算法分析该算例，其中CC的混沌控制因子设为0.05，DSTM的混沌控制因子设为0.05，0.1和0.2三种情况。

由于该算例的变量数达到8个，不适合在U空间内呈现MPP搜索路径，因此建立了如图5所示的可靠度指标β随迭代次数的变化曲线。其中图5(a)显示了HL-RF，iHL-RF，CC和AASTM四种算法的计算结果，图5(b)显示了DSTM在三种混沌控制因子下的计算结果，并与AASTM的结果进行了比较。从图5(a)可以看出，HL-RF算法的计算结果会发生周期为2的振荡，而iHL-RF，CC和AASTM三种算法能够迭代收敛，且从迭代历程可以看出，AASTM和iHL-RF完成收敛的迭代次数小于30，而CC的迭代次数较多。从图5(b)可以看出，DSTM在不同的混沌控制因子下，会出现不同的迭代效果，混沌控制因子在λ=0.2时会出现周期振荡，而较小的混沌控制因子(λ=0.05和λ=0.1)均能保证迭代收敛，且λ=0.1时完成收敛的迭代次数较少，但比AASTM的迭代次数多。

表2 算例2的随机变量分布情况

Tab.2 Distributions of the random variables for example 2

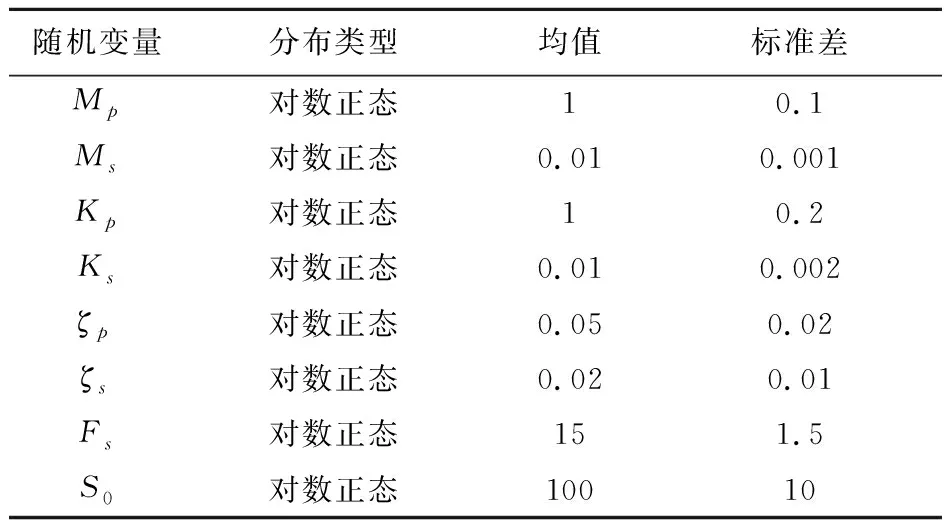
随机变量分布类型均值标准差Mp对数正态10.1Ms对数正态0.010.001Kp对数正态10.2Ks对数正态0.010.002ζp对数正态0.050.02ζs对数正态0.020.01Fs对数正态151.5S0对数正态10010

表3比较了算例2在各算法下最终的迭代结果，HL-RF和DSTM(λ=0.2)最终得到周期振荡解，而iHL-RF，CC，DSTM(λ=0.05)，DSTM(λ=0.1)和AASTM最终得到的可靠度指标β基本一致，相比之下AASTM的函数计算次数最少，即计算效率最高。

5.3 屋架算例

图6(a)是一个受均布载荷q(单位：N/m)作用下的屋架结构[25]，该结构为对称结构，中上弦杆(AD、DC、CF和FB)和受压腹杆(DE和FG)的材料为钢筋混凝土，而下弦杆(AE、EG和GB)和受拉腹杆(CE和CG)的材料为钢。均布载荷q可以等效为节点载荷P=ql/4，屋架的各尺寸参数如图6(b)所示。将屋架顶端C的垂直挠度不超过0.03 m作为约束条件，可得该结构的极限状态函数为

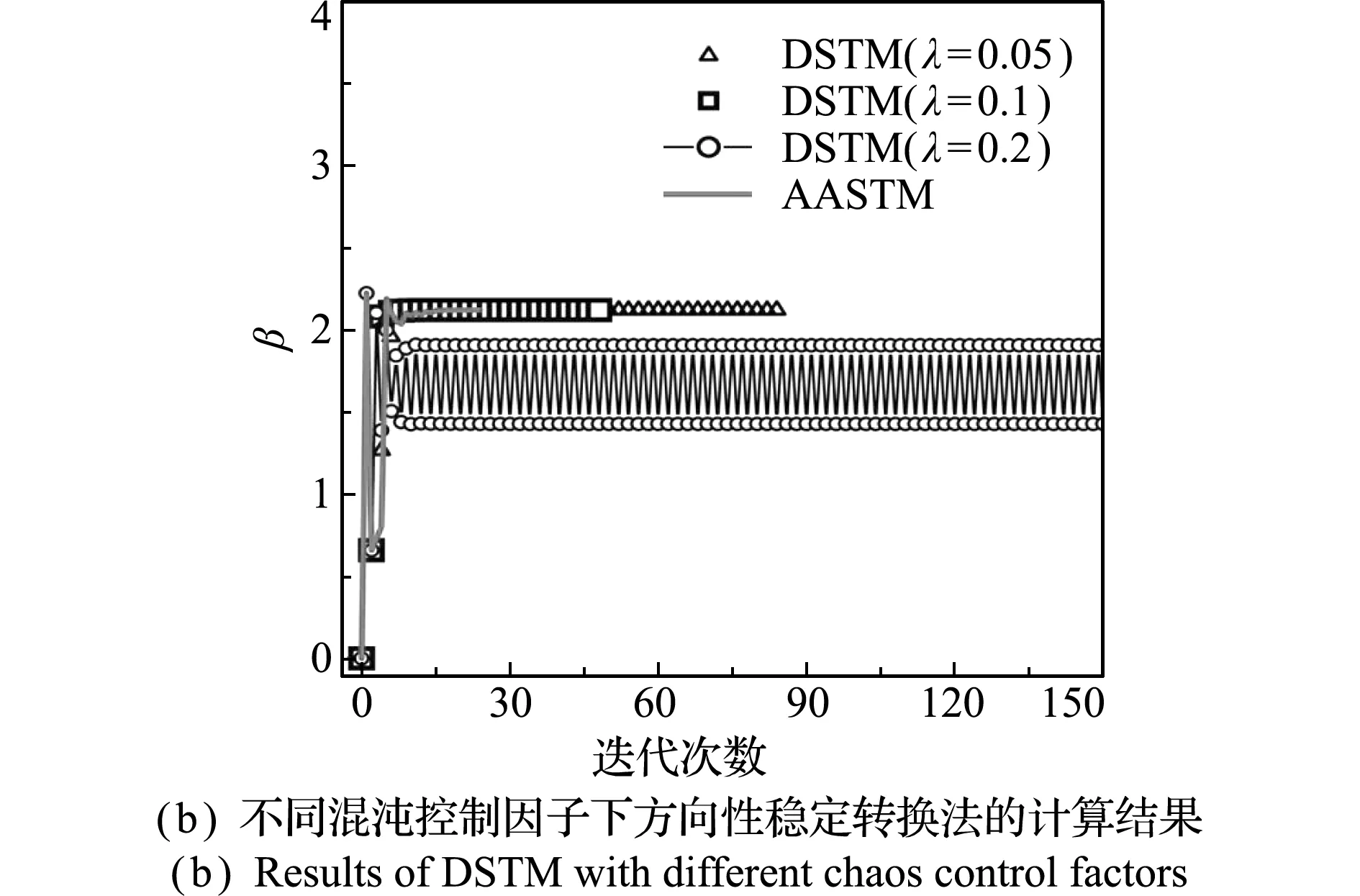
图5 算例2的可靠度指标迭代历程

Fig.5 Iteration history of reliability index for example 2

表3 算例2计算结果

Tab.3 Results for example 2

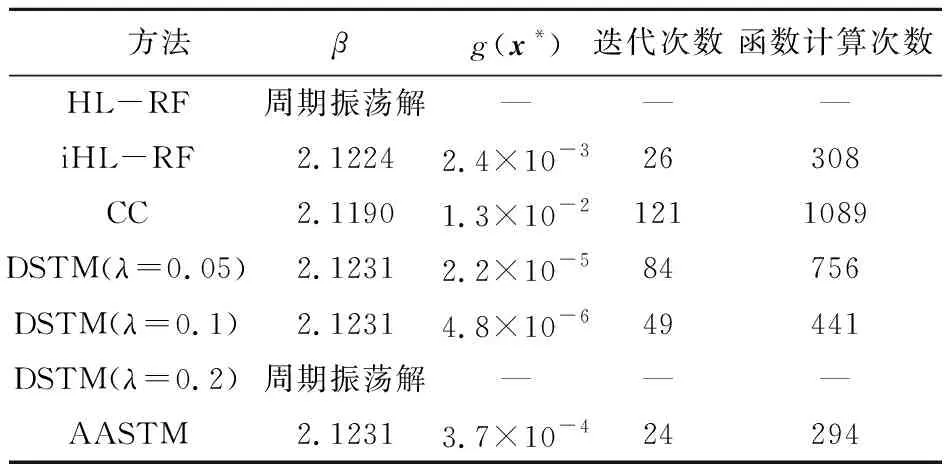
方法βg(x*)迭代次数函数计算次数HL-RF周期振荡解———iHL-RF2.12242.4×10-326308CC2.11901.3×10-21211089DSTM(λ=0.05)2.12312.2×10-584756DSTM(λ=0.1)2.12314.8×10-649441DSTM(λ=0.2)周期振荡解———AASTM2.12313.7×10-424294

(17)

式中Ac和Ec分别为材料是钢筋混凝土的杆件截面积和弹性模量，As和Es分别为材料是钢的杆件截面积和弹性模量，l为屋架跨度。该算例包含 6个 服从正态分布的随机变量，其分布参数列入表4。采用五种算法分析该算例，其中CC和DSTM的混沌控制因子设为0.05。

由于变量数较多，该算例同样需要通过可靠度指标β随迭代次数变化曲线呈现迭代历程，如图7所示。可以看出，所有算法都能迭代收敛，但完成收敛的迭代次数不同，其中CC算法迭代次数在120左右，而其他四种算法的迭代次数小于60。通过局部放大图可知，HL-RF，iHL-RF和AASTM的迭代次数小于6，其中AASTM和iHL-RF的迭代点完全重合。

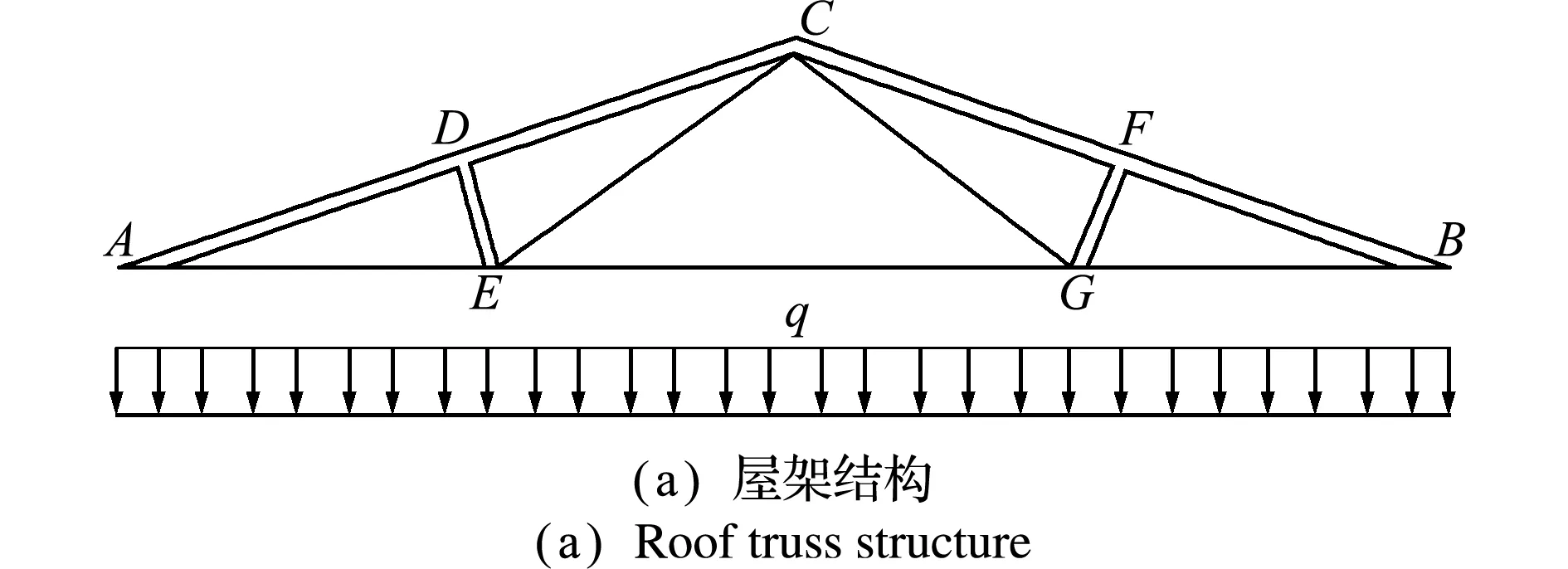
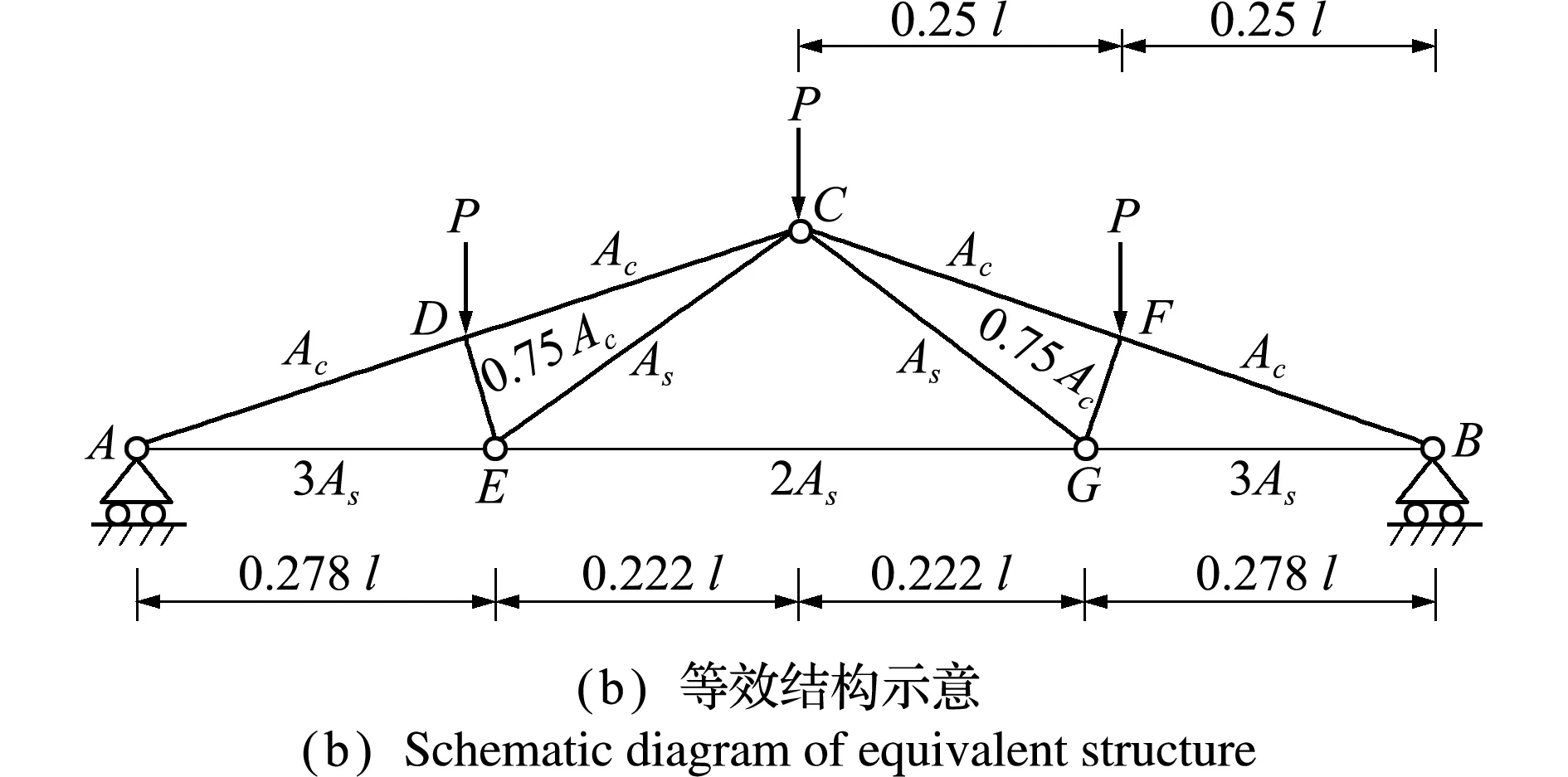
图6 屋架算例示意

Fig.6 Schematic diagram of roof truss example

表4 算例3的随机变量分布情况

Tab.4 Distributions of the random variables for example 3

随机变量分布类型均值标准差q/(N·m-1)正态200001400l/m正态120.12Ac/m2正态9.82×10-45.9852×10-5Ac/m2正态0.040.0048Es/Pa正态1×10116×109Ec/Pa正态2×10101.2×109

由表5可知，除CC算法外，算例3在其他四种算法下求得的可靠度指标均为2.4212。将随机变量的均值代入式(17)，可得均值点对应的极限状态函数值g0=6.6×10-3，接近于0，因此该算例取g(x*)/g0表征各算法求得的MPP与极限状态面的接近程度。CC算法的g(x*)/g0值是其他算法的102～105倍，可见混沌控制因子为0.05使CC算法出现了收敛早熟现象，且收敛效率很低(函数计算次数为805)。由于该算例的非线性程度不高，采用HL-RF算法可以很快收敛(函数计算次数为35)，而DSTM算法的计算效率(函数计算次数为392)同样受混沌控制因子过小的影响。iHL-RF和AASTM算法的迭代结果相同，且计算效率并列第一(函数计算次数均为33)。

5.4 飞机加筋板屈曲算例

图8是含多个圆形开孔和多条曲筋的加筋板[26]，又称曲筋板，最初由NASA设计、制造及测试[27]，主要用于飞机发动机吊架肋翼。曲筋板的长和宽分别为711.2 mm和609.6 mm，板中含有4条曲筋和2个圆形开孔，圆孔周边由厚圆环加强，其中大小圆孔的圆环宽度分别为10.55 mm和10.25 mm，圆环厚度分别为5.9 mm和4.7 mm。板材属性为弹性模量E=72504 MPa，泊松比υ=0.33，密度ρ=2.8×10-9t/mm3。曲筋板的筋条高度h、筋条厚度tc和蒙皮厚度t设为随机变量，均服从正态分布，且分布参数列入表6。屈曲是薄壁结构的主要失效模式，将曲筋板的抗屈曲承载能力低于37850 N作为失效条件，可得该结构的极限状态函数为

图7 算例3的可靠度指标迭代历程

Fig.7 Iteration history of reliability index for example 3

表5 算例3计算结果

Tab.5 Results for example 3

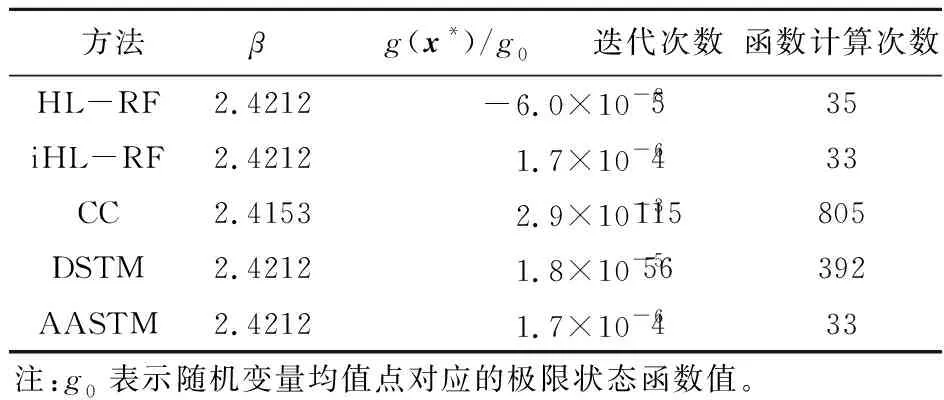
方法βg(x*)/g0迭代次数函数计算次数HL-RF2.4212-6.0×10-8535iHL-RF2.42121.7×10-6433CC2.41532.9×10-3115805DSTM2.42121.8×10-556392AASTM2.42121.7×10-6433注:g0表示随机变量均值点对应的极限状态函数值。

g=Pc r-37850

(18)

式中Pc r为曲筋板的抗屈曲承载能力，可通过线性屈曲分析求得。由于通过有限元方法进行线性屈曲分析较耗时，本文采用Kriging代理模型来提高计算效率。通过最优拉丁超立方抽样和有限元分析生成100个样本点(三个随机变量作为输入，Pc r作为输出)，用于构造Kriging代理模型。通过校验可得代理模型与有限元分析的相对误差低于1%，可见Kriging代理模型可以准确预测曲筋板的抗屈曲承载能力。基于该代理模型，采用五种算法对此算例进行可靠度分析，其中CC和DSTM的混沌控制因子设为0.05。

由表7可以看出，五种算法求得的可靠度指标均为2.3549，但CC和DSTM的g(x*)值是HL-RF，iHL-RF和AASTM的102～103倍，可见HL-RF，iHL-RF和AASTM求得的MPP更靠近极限状态面。由函数计算次数分析计算效率可知，HL-RF，iHL-RF和AASTM的函数计算次数最少，计算效率高于CC和DSTM。该算例表明，HL-RF算法和AASTM均可以高效求解，验证了AASTM的鲁棒性。

图8 飞机加筋板

Fig.8 Aircraft stiffened shell

表6 算例4的随机变量分布情况

Tab.6 Distributions of the random variables for example 4

随机变量分布类型均值标准差h/mm正态180.9tc/mm正态1.360.068t/mm正态2.360.118

表7 算例4计算结果

Tab.7 Results for example 4

方法βg(x*)迭代次数函数计算次数HL-RF2.35496.7×10-4520iHL-RF2.35496.7×10-4520CC2.35491.3×10-1226904DSTM2.35491.9×10-2105420AASTM2.35496.7×10-4520

6 结 论

本文提出了基于Armijo准则的自适应稳定转换法，根据Armijo准则对方向性稳定转换法进行了改进，自适应合理选取每个迭代步的混沌控制因子，使每步尽量高效收敛。针对方向性稳定转化法无法主动控制振荡的情况，本文的AASTM算法采用混沌控制方法对振荡进行控制，有利于提高算法鲁棒性。对不同非线性程度的低维或高维问题均有较好的收敛性，验证了本文算法在计算效率和鲁棒性上可以实现更好的性能平衡，有利于使结构可靠度分析更高效和稳健。