基于六面体网格的向量式有限元分析及应用

， ，

(1.浙江省建筑设计研究院，杭州 310006；2.浙江大学 空间结构研究中心，杭州 310058)

1 引 言

实体结构是最为通用的结构形式，具有广泛的工程应用。实体单元与其他单元通过在表面连接，以模拟任意外形结构在外界作用下的响应。根据单元形式的不同，实体结构单元主要有四面体和六面体两类，前者适用性强，而后者计算精度较高[1,2]。Pawlak等[3]推导了含有旋转自由度的四面体单元形式，该单元对于具有反对称应力和旋转问题的结构计算具有较高精度。Tayloy等[4]提出位移不协调的非协调六面体单元形式，并通过等参变换实现不规则网格的数值模拟。Cao等[5]基于Hu-Washizu变分原理提出多变量形式的六面体单元，提高了单元抗网格畸变能力。李宏光等[6]引入体积坐标方法，利用其与整体坐标的线性关系，构造出对网格畸变不敏感的六面体单元，以应用于复杂结构形状。对于大位移大转动问题，六面体单元通过较少的单元网格划分即可获得较为精确的结果。

向量式有限元VFIFE(vector form intrinsic finite element)[7-9]是基于质点运动和向量分析的新型数值方法。该法基于牛顿经典运动理论，以质点系的运动来描述结构体系的行为，各质点间的运动相互独立并通过逐步计算求得整体结构响应，而且求解时不存在迭代和刚度矩阵问题。在变形坐标系下，刚体位移可能造成的误差采用逆向运动方式来规避。故该方法在结构大位移大转动、机构运动及不连续行为的数值分析领域具有较好的应用[10-14]。

本文给出了八节点六面体等参实体单元的向量式基本理论，采用参考面的逆向运动求解节点纯变形，通过单元形函的虚功方程计算节点内力，针对坐标模式和内力积分模式等特殊问题提出了有效的处理方案。编制数值计算程序，并通过结构算例验证理论和程序的正确性和实用性。

2 六面体网格的向量式理论

向量式有限元是由质点和单元组成，结构的质量仅分布于质点，本文单元为八节点六面体等参实体单元。求解步骤为质点全位移计算、单元节点纯变形计算和单元节点内力计算，通过循环来达到逐点逐步求解。分析流程如图1所示。

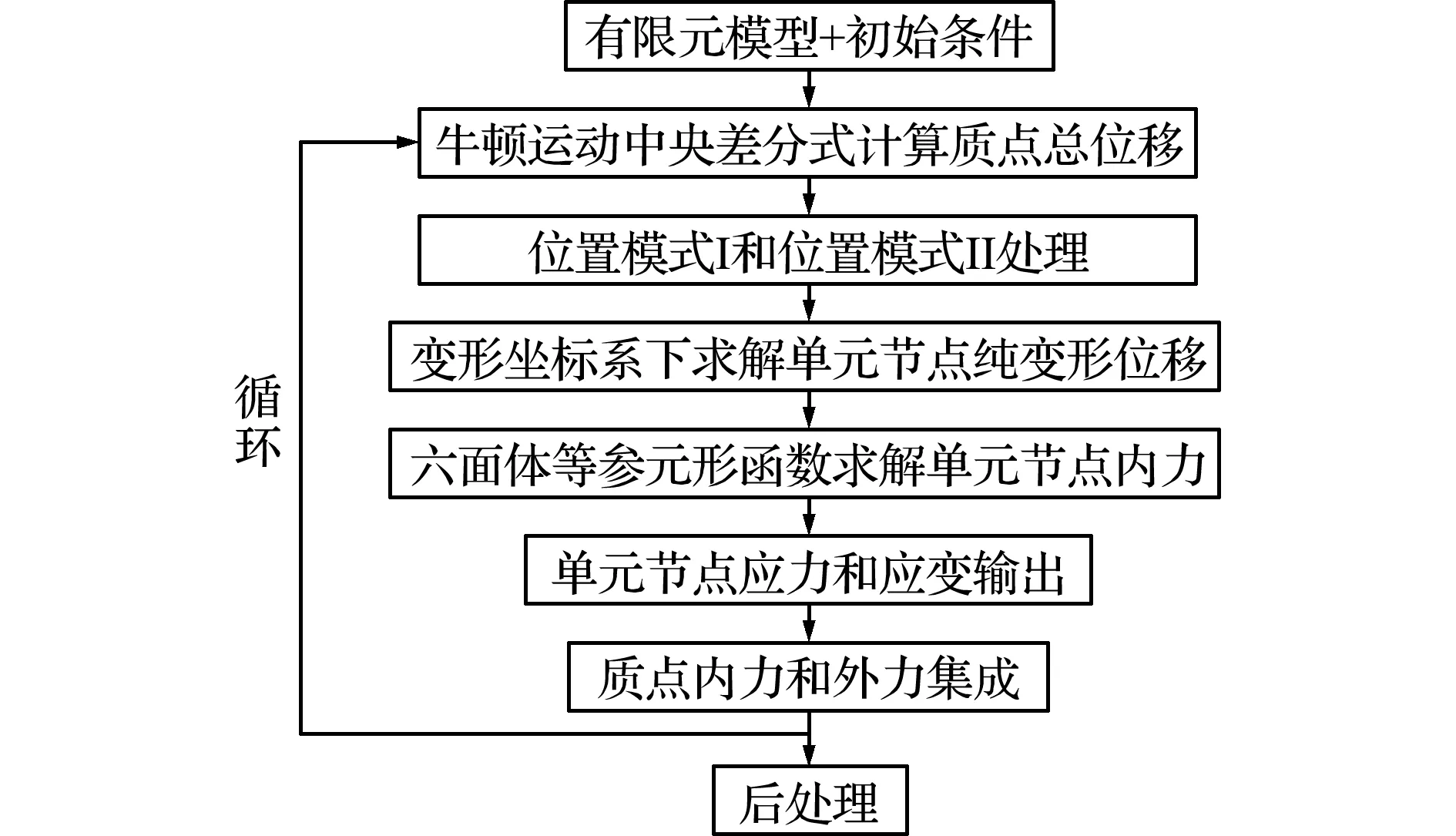
图1 分析流程图

Fig.1 Analysis flow chart

2.1 质点全位移

质点的运动满足微分方程：

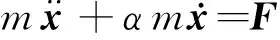
(1)

式中m为质量，α为阻尼参数，x为位移向量，F=fext+fint为合力向量，上标ext和int分别表示外力和内力。

时间步内的质点全位移采用显式中央差分方法数值求解运动方程获得，为质点新坐标与初始坐标的差值。

2.2 单元节点纯变形

(1) 坐标模式的转换

通过参考平面的逆向运动，在质点全位移中去除刚体位移，以获得节点纯变形。节点实际坐标所组成六面体的每个面均是空间曲面四边形，采用投影方式将每个面均投影为平面四边形，组合后为投影六面体(即坐标模式I)，详见第3.1节。

六面体单元面i(i=1～6)的节点j(j=1,2,3,4)的实际坐标向量记为xj，则平均法向量ni为

(2)

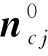
ni x(x-xC i)+ni y(y-yC i)+ni z(z-zC i)=0

(3)

(4)

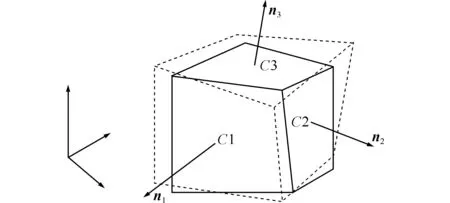
图2 六面体单元的投影位置

Fig.2 Projection position of the hexahedral element

(2) 刚体运动的估算

获得投影六面体后，采用参考平面估算刚体运动(平移和转动)，取投影六面体单元的abcd面为参考平面,如图3所示。

参考平面abcd在t0～t时段的空间运动包括平移、转动和纯变形[15]。

平移取参考面节点a的全位移ua，则消去平移后的质点位移为

(5)

利用参考面估算质点的逆向面外转动位移

(6)

质点i(i=a～h)的逆向面内转动位移为

(7)

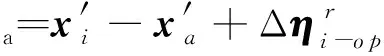
质点纯变形是通过在质点全位移中消去平移和转动(面外和面内)后获得，

(8)

2.3 单元节点内力

(1)传统形函的引入

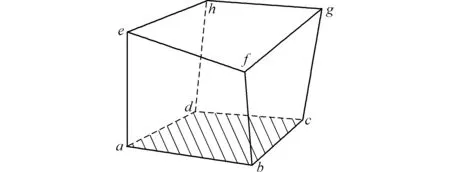
图3 投影六面体单元及其参考平面

Fig.3 Projective hexahedral element and its reference plane

将整体坐标系转换至变形坐标系，即

(9)

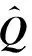
节点的纯变形向量为

(10)

节点的纯变形组合向量为

(11)

(12)

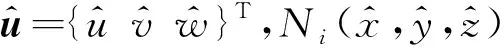
(13)

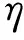
采用雅可比矩阵J将变形坐标系转换至局部坐标系，参考文献[16]。

(14)

(15)

(2) 虚功方程的求解

单元变形满足虚功方程

(16)

式中fi为整体坐标系下的节点内力。

由应力应变描述的变形虚功为

(17)

单元节点的内力向量为

(18)

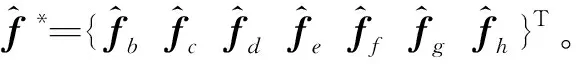
(19)

将虚拟状态时的节点内力分量转换至实际状态，并经正向运动，求得实际位置时的节点内力：

(20)

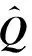
单元作用于质点的内力finti通过节点内力fi反向作用并集成获得。

3 关键问题的处理

3.1 坐标模式

(1) 节点坐标模式

单元节点坐标(坐标模式I)用于求解时间步内的节点纯变形和内力，因而单元各面上节点均需处于同一平面。

(2) 质点坐标模式

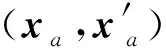
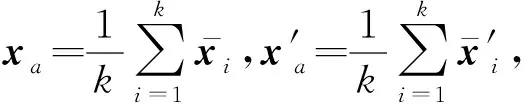
3.2 内力积分

六面体单元内部的应力应变随位置变化，求解虚功方程时需采用数值积分计算。采用三维高斯积分方案[1]时，单积分点和8积分点的相关系数列入表1，本文采用后者求解式(18)，可获得较好计算结果。

表1 数值积分方案

Tab.1 Numerical integration programmes

积分点数焊iηiζiHijm10008.08±1/3±1/3±1/31.0,1.0,1.0,1.01.0,1.0,1.0,1.0

(21)

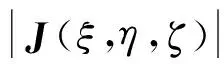
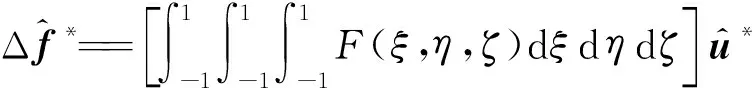
(22)

式中k为每个坐标方向的积分点数。

4 工程结构算例分析

基于向量式有限元六面体等参元理论，在Matlab平台上编制分析计算程序，实现向量式有限元实体结构的计算分析。

4.1 悬臂梁结构静动力分析

(1) 静力分析

悬臂梁顶面施加竖向均布静力作用q=2.5×104kN/m2，采用斜坡-平台方式缓慢加载，并考虑阻尼效应来获得收敛值。细长梁自由端的挠度理论解为

w(x)=(x2-4Lx+6L2)(qH)x2/(24EI)

图5为悬臂梁自由端顶部节点竖向位移的计算收敛过程，图6为沿悬臂梁顶部中线各节点的竖向位移和von Mises应力结果。可以看出，竖向位移和von Mises应力结果与细长梁理论解及ABAQUS结果均基本一致。本文和ABAQUS的自由端节点竖向位移分别为0.0115 m和0.0119 m，相对理论解0.0117 m的误差分别为-1.71%和1.71%。本文和ABAQUS的自由端节点von Mises应力分别为38.06 MPa和36.4 MPa，差异约为4.36%，悬臂端节点由于应力集中，结果差异相对较大，约为9.8%。可见本文方法在实体工程结构静力分析中具有较好准确性。

(2) 动力分析

在悬臂梁顶面施加瞬时动力均布荷载q=2.0×104kN/m2，不考虑阻尼效应。取t=0.01 s进行分析，图7和图8分别为自由端顶部节点竖向位移和von Mises应力随时间的变化情况。

结果表明，本文位移和应力结果均与ABAQUS结果吻合较好，验证了本文方法在实体工程结构动力分析中的准确性。图8中两者应力结果的总体变化趋势基本一致，由于端部应力集中，局部振荡波形有所差异。

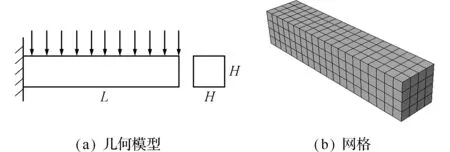
图4 悬臂梁模型

Fig.4 Cantilever-beam model

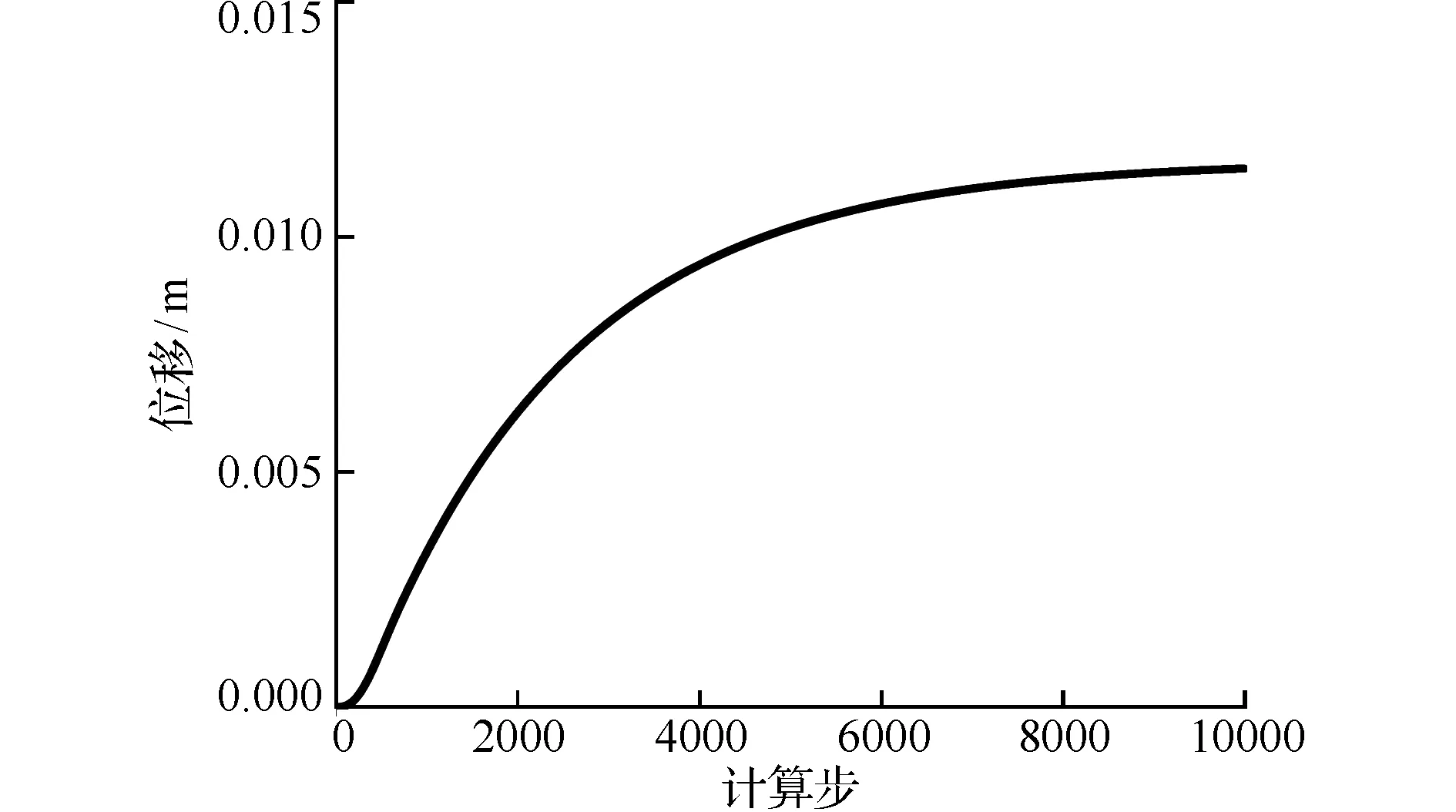
图5 自由端竖向位移收敛过程

Fig.5 Convergence process of free end vertical displacement

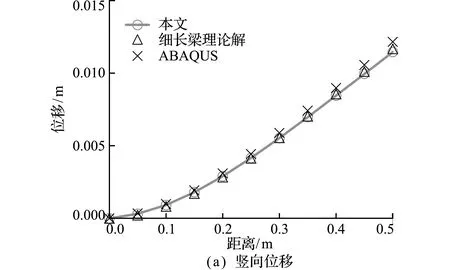
图6 顶部中线位置结果

Fig.6 Results of the top center-line

4.2 环形套筒大变形分析

取t=0.02 s进行分析。图10为环形套筒左侧中心节点的水平位移随时间的变化情况。可以看出，本文方法可获得套筒大变形过程中的位移变化情况，且与ABAQUS结果基本一致。在同时采用显式动力分析时，本文方法由于不存在刚度矩阵奇异和迭代不收敛问题，相比ABAQUS具有更高的计算效率。

典型的环形套筒变形和von Mises应力云图情况如图11所示。可以看出，套筒起初表现为压扁变形(t=0.004 s)，t=0.008 s时，压扁变形达到最大值；接着套筒开始回弹，在t=0.012 s时回弹至最小变形；然后，套筒压扁变形再次变大(t=0.015 s)；依此循环往复。本文所得结构变形和应力分布情况均与ABAQUS计算结果吻合。

图7 自由端竖向位移-时间曲线

Fig.7 Vertical displacement-time curves of the free end

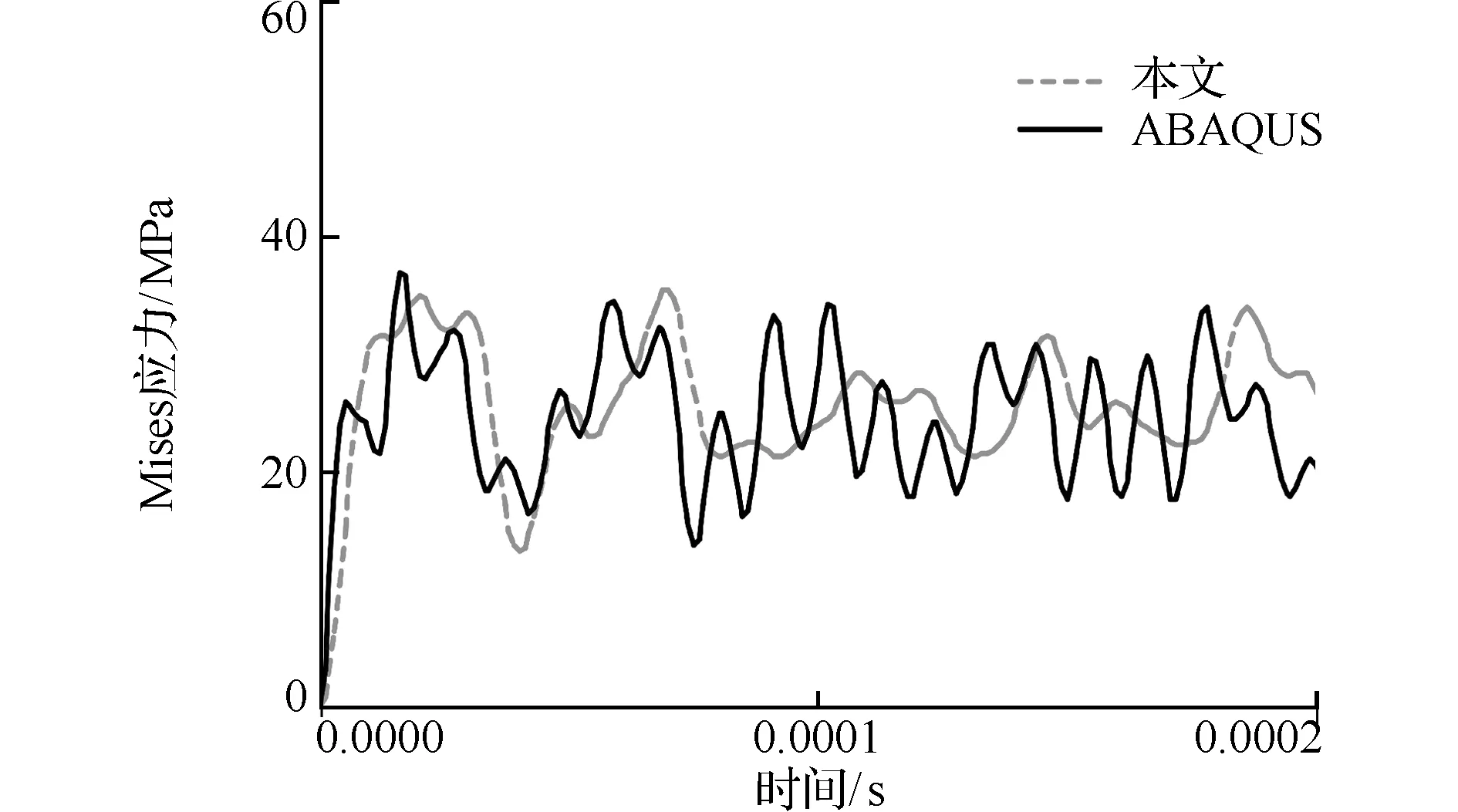
图8 自由端von Mises应力-时间曲线

Fig.8 Von Mises stress-time curves of the free end

图9 环形套筒模型

Fig.9 Annular sleeve model

图10 左侧中心节点的位移-时间曲线

Fig.10 Displacement-time curves of the left central node

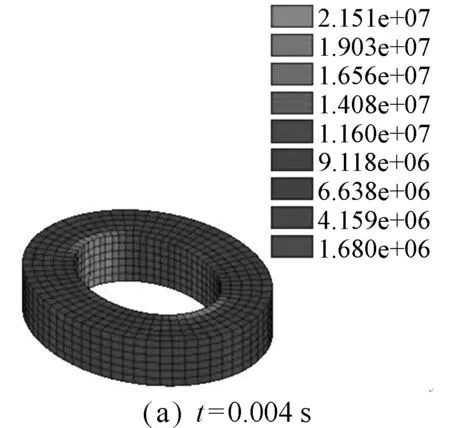
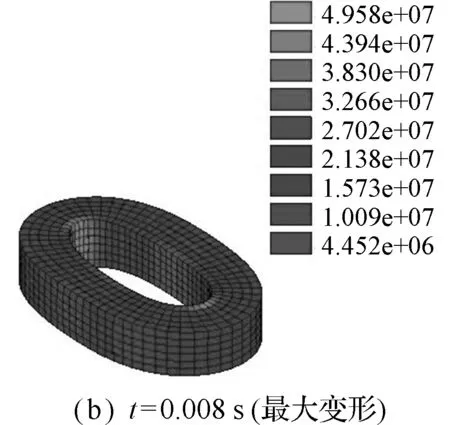
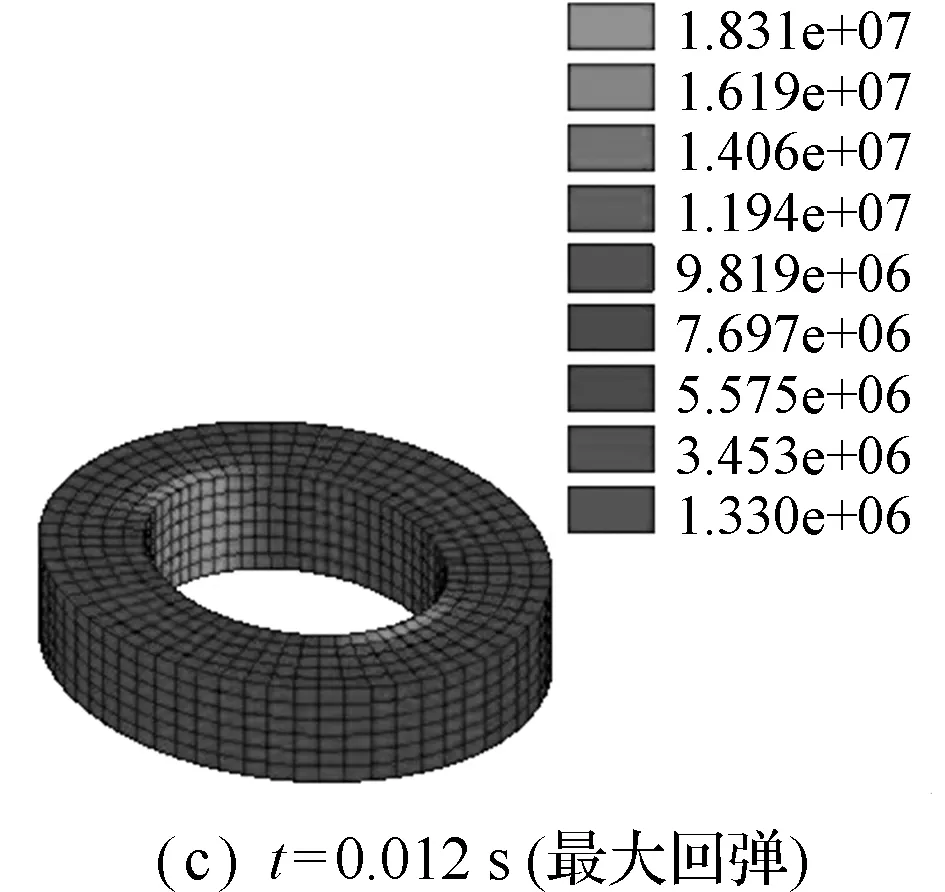
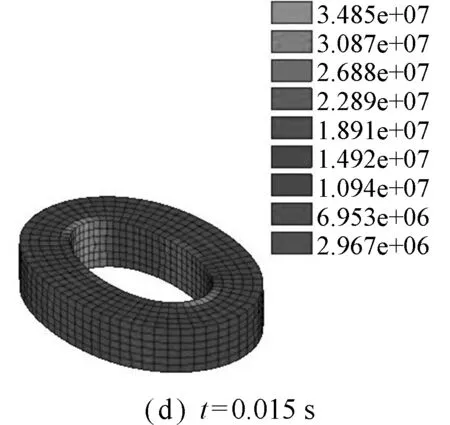
图11 环形套筒压扁变形图

Fig.11 Flattened deformation diagrams of annular sleeve

5 结 论

基于向量式有限元，给出了八节点六面体等参实体单元的基本公式，通过投影方式将空间曲面六面体转换为投影六面体，采用参考面的逆向运动求解节点纯变形，通过单元形函的虚功方程计算节点内力。针对坐标模式和内力积分模式等关键问题提出了有效的处理方案。

编写了六面体实体单元的数值计算程序，并针对工程结构的悬臂梁静动力和环形套筒大变形算例进行分析，验证了本文理论和程序的正确性和实用性。

向量式有限元适用于分析工程结构大变形大位移行为的动力分析，求解时不存在迭代和刚度矩阵问题，在结构动力分析领域具有更高的效率和准确性。