考虑高阶振型的超高层建筑风致位移响应研究

李阳阳,陈园园，冯松宝，孙 磊，张萍花

1.宿州学院资源与土木工程学院，宿州,234000 2.安徽省煤矿勘探工程技术研究中心，宿州,234000;3.宿州学院化学化工学院,宿州,234000

十九世纪初期，大多数建筑的高度不高，平面和竖向布置较为规则，此类结构的主要振动表现为平面方向的侧向振动，且各振型频率之间比较稀疏。因此，当时计算高层建筑风致响应的方法，如阵风荷载因子法(Gust Loading Factor，GLF)[1-4]以及我国荷载规范的惯性风荷载法[5]，出于公式简化和方便使用，均是仅考虑结构基频振型的影响，而忽略高阶振型对结构风致位移响应的贡献。

然而，随着我国经济实力的快速增长和建筑设计施工技术的不断更新，近年来，我国的建筑高度不断被刷新，如2014年竣工的上海中心(632 m)、2017年竣工的深圳平安金融中心(599 m)、2015年竣工的天津117大厦(596.5 m)和2016年竣工的广州周大福金融中心(530 m)。随着建筑高度的增加和阻尼的变小，结构的自振频率变得越来越低，高阶振型频率则可能会位于风压功率谱的主要频带内[6-9]，此时高阶振型对结构风致位移响应的贡献则不可忽略，计算超高层建筑的风致位移响应时需要考虑高阶振型的影响。

本文以珠海市某一超高层建筑的初步设计方案为研究对象，分别采用完全二次项组合(CQC)方法和平方和开平方根(SRSS)方法计算得出高阶振型的风致位移响应，然后将考虑高阶振型的结构风致位移响应与仅考虑基频振型的结构风致位移响应进行比较，分析两者之间存在的差异，最终得出高阶振型对超高层建筑风致位移的影响。

1 风致位移响应计算公式

1.1 基本假设

风对结构的作用机理十分复杂，计算风致位移响应的理论公式都是基于一定的假设进行推导，主要假设如下：

(1)准定常假设

建筑物表面Mi(x,z)位置t时刻的脉动风压w(x,z,t)可用下式表达[10]：

(1)

(2)片条假设

建筑物表面z高度t时刻的脉动压力p(z,t)为：

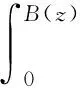
(2)

(3)平均风速采用指数形式

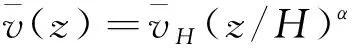
(3)

1.2 公式推导

结构总的风致位移响应包括脉动风作用下结构的响应和平均风作用下结构的响应两部分，与结构动力特性(质量、阻尼比、频率、振型)相关的是脉动风作用下结构的响应，平均风作用下结构的响应与其无关。风致位移响应与其响应方差仅差一个峰值因子，故由响应方差来代表风致位移响应。本节对风致位移响应方差的理论公式进行简要的说明。

根据随机振动的理论知识[11]，位移响应功率谱密度Sy(z,n)为：

(4)

式(4)中，φj(z)和φk(z)分别表示第j阶和第k阶振型z高度处的坐标，Hj(-in)和Hk(in)为复频响应函数，表达式见公式(5)，SFjFk(n)为第j振型和第k振型的广义力互谱密度，表达式见公式(6)：

(6)

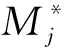
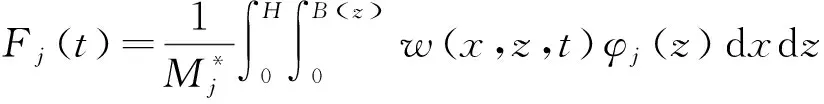
(7)

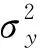
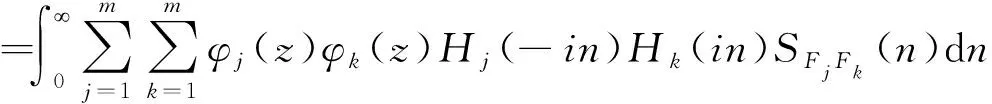
公式(8)是CQC方法，是一种准确计算结构风致位移响应方差的方法。如果忽略公式(8)中第j振型与第k振型的交叉项时，式(8)可写作：

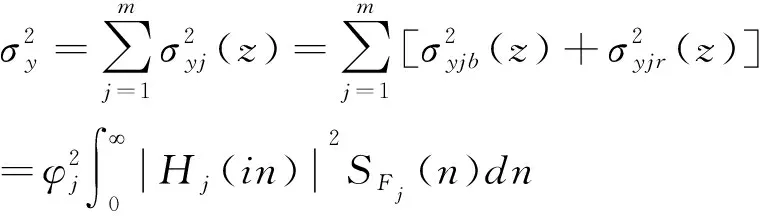
(9)

式(9)中，σyjb(z)为背景响应的根方差，σyjr(z)为共振响应的根方差，此时则为SRSS方法。

2 典型工程算例分析

以珠海市某一超高层建筑为工程背景，结合多点同步瞬态测压技术(SMPSS)测得模型表面的风压时程，分别采用CQC方法和SRSS方法计算得出高阶振型的风致位移响应，同时与只考虑基频振型的风致位移响应进行对比，得出高阶振型对风致位移响应的影响。风向角定义见图1。

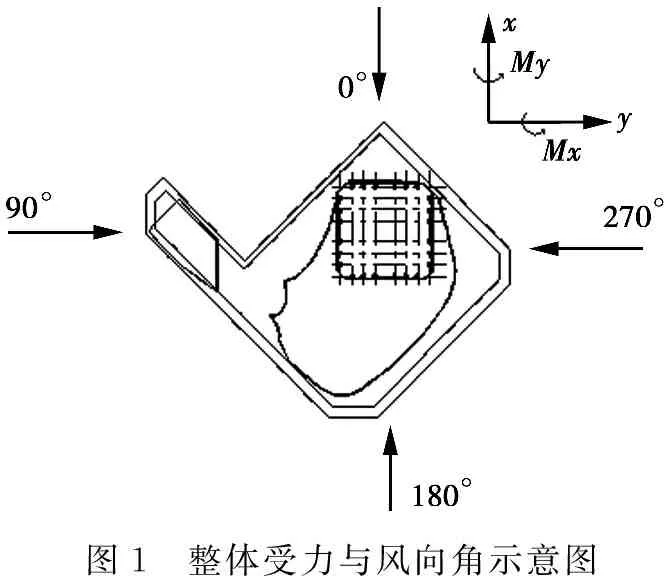
图1 整体受力与风向角示意图

2.1 结构动力特性

结构动力特性(质量、阻尼比、频率、振型)的参数值均来自武汉设计院，并根据盈建科建筑结构设计软件计算得出。阻尼比采用0.04，由建筑结构荷载规范可得珠海市的基本风压为0.85 kPa，结构的各阶振型频率和广义质量如表1所示。

表1 结构的振型频率及广义质量

2.2 位移响应根方差

在0°、90°、180°、270°四个特殊风向角下，本节分别根据FM方法(只考虑基频振型)、CQC方法和SRSS方法，结合公式(4)—(9)，采用Matlab自行编写的程序计算，得出了前三阶振型在X、Y、Z三个方向的脉动位移响应根方差σyx、σyy、σyz，如图2所示。

全风向角(0°～350°)X、Y和Z方向顶部脉动位移响应根方差误差，如图3所示。误差Δy的定义如下：

(10)

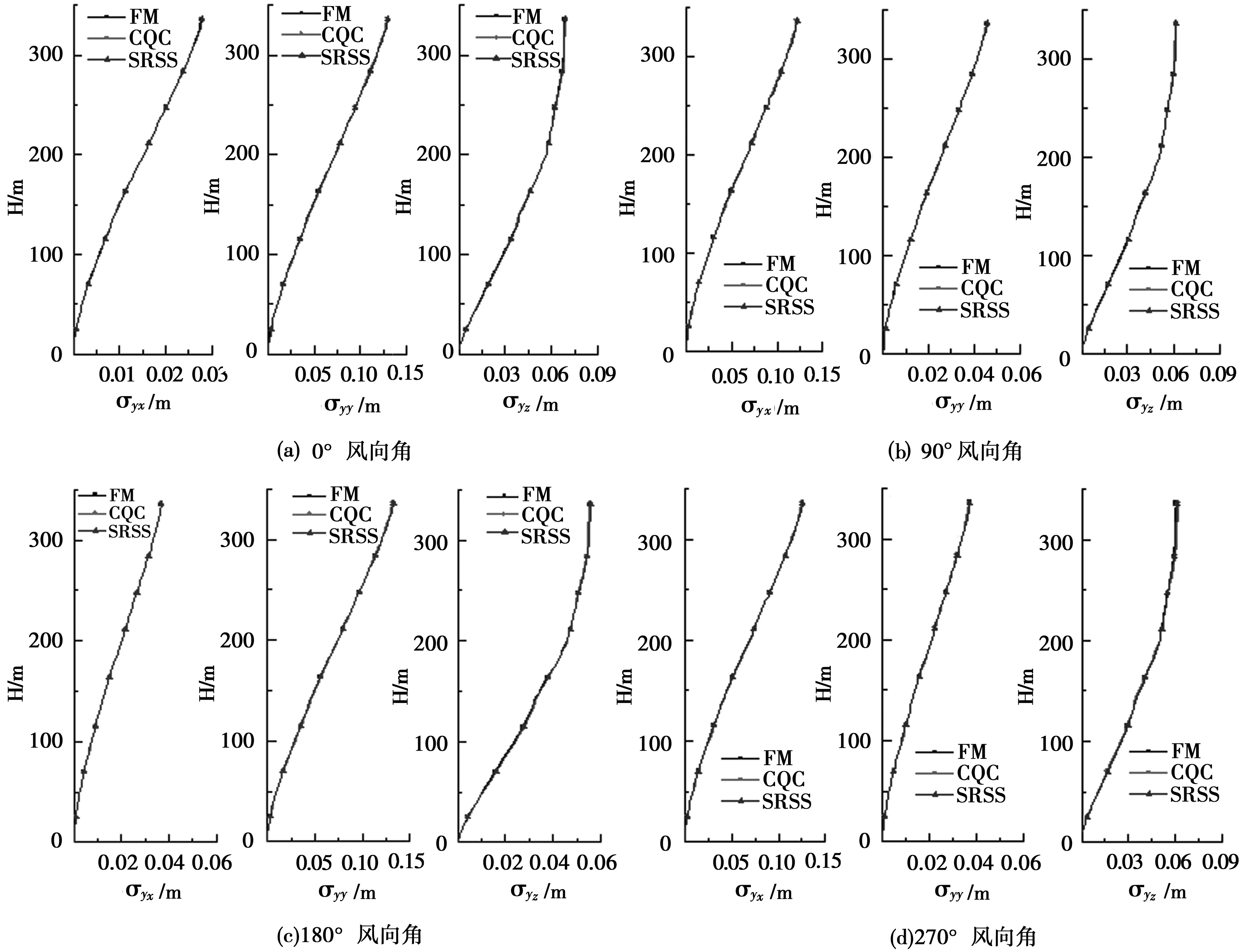
图2 特殊风向角X、Y和Z方向位移响应根方差

从图2中可得出：四个特殊风向角(0°、90°、180°、270°)下，X、Y、Z三个方向分别按三种方法(FM、CQC、SRSS)计算得到的位移响应根方差沿高度方向的差异很小，三种方法得到的根方差分布图基本重合。对于风致位移响应，基频振型起着控制作用，高阶振型的影响可以忽略不计，计算风致位移响应时，只需考虑基频振型的响应就可以达到工程要求，而不需要采用繁琐的CQC方法或SRSS方法考虑高阶振型的影响。

从图3可进一步得出顶部的位移响应根方差的分布规律：

(1)X方向，FM方法最大误差为1.08%，最小误差为-0.36%；SRSS方法最大误差为1.11%，最小误差为-0.31%。Y方向，FM方法最大误差为0.91%，最小误差为-0.03%；SRSS方法最大误差为0.94%，最小误差为0.05%。Z方向， FM方法最大误差为0.41%，最小误差为-2.60%；SRSS方法最大误差为0.92%，最小误差为-2.11%。

图3 全风向角X、Y和Z方向的顶部位移响应根方差误差

(2)对于脉动位移响应根方差，水平方向(X、Y方向)的误差总体上小于扭转方向(Z方向)的误差。与精确的CQC方法相比，FM方法的计算误差在X、Y、Z三个方向的最大误差分别为1.08%、0.91%、2.6%，且均不大于5%，满足工程误差要求。

(3)相比于顺风向的位移响应根方差，横风向附近出现了相对较大的误差。90°和270°风向角附近，X方向产生了较大的误差；0°和180°风向角附近，Y方向产生了较大的误差。

3 结 语

以珠海市某一超高层建筑为研究对象，得出如下结论：

(1)对于超高层建筑的风致位移响应，基频振型起着控制作用，高阶振型的影响可以忽略不计。计算风致位移响应时，不需采用繁琐的CQC方法或SRSS方法来考虑高阶振型的影响，只需考虑基频振型就可满足工程要求。

(2)对于脉动位移响应根方差，水平方向(X、Y方向)的误差总体上小于扭转方向(Z方向)的误差。

(3)相比于顺风向的风致位移响应，高阶振型以及振型间的耦合效应对于横风向的风致位移响应影响更大。与风向一致方向的位移响应根方差相比，风向垂直方向附近的位移响应根方差出现的误差相对较大。