正常人体步态的动力学仿真与分析

徐中华,方 娟,陈隆飞,穆载乐

(江南大学机械工程学院,江苏 无锡 214122)

0 引 言

近年来，随着人们生活节奏的加快和工作压力的增大，人们经常进行无规律的饮食和休息，这造成了包括脑卒中在内的诸多老年疾病的发病趋于年轻化。卒中后偏瘫患者在运动、感觉、语言、认知等功能方面存在不同程度的障碍，其中最常见的是行走能力的损伤[1-2]。行走障碍严重影响了患者个人的生活质量,也给患者家庭带来了沉重的负担。

传统的步态康复治疗需要耗费大量的人力和时间，而且治疗效果受康复理疗师水平的影响，训练效果难以得到保证。随着医疗技术的日益发展，出现了康复机器人技术并得到了大力发展。经临床试验表明，步态康复机器人能够有效地改善传统治疗方法面临的问题[3-4]。同时在结合如功能性电刺激[5-6]、虚拟现实技术[7]等治疗方法的基础上，机器人能够对患者进行更加高效的康复训练。

文献[8]指出，髋关节、膝关节和踝关节的力矩为研究运动过程中下肢各个部位之间的动态相互作用提供了重要的依据。为便于对下肢进行模块化和参数化设计，本文采用Simulink中的SimMechanics作为仿真工具。孟明等[9]利用SimMechanics建立了单侧下肢二连杆仿真模型，得到了髋关节和膝关节力矩。刘小龙等[10]利用ADAMS和MATLAB分别对下肢外骨骼的单腿支撑和双腿支撑的模型进行联合动力学仿真，得到髋关节和膝关节力矩。唐志勇等[11]将人体下肢简化成七连杆机构，利用MATLAB仿真得到下肢各关节的力矩和功率，将结果作为下肢外骨骼ADAMS模型的输入进行了仿真验证。陈贵亮等[12]利用Solidworks和MATLAB对下肢外骨骼康复机器人进行联合仿真，得到髋关节和膝关节力矩，并用BP神经网络对模型进行了辨识仿真。张燕等[13]利用ADAMS建立了人体下肢模型，对不同路况下的下肢运动进行运动学仿真。在以上大多数研究中踝关节、足部以及地面反力在下肢运动过程中的作用被忽略，直接将其视为一质点。当前运动捕捉技术有了很大的进步，这为仿真工作提供了重要的数据支撑[14-15]。然而以上研究并未将仿真结果与实际实验数据对比，无法得知结果的正确性。因此本文对下肢动力学模型进行了改进，将踝关节、足部以及地面反力对下肢运动的作用都考虑进去，同时结合真实实验的采集数据对正常人体步态展开深入的仿真分析。

1 方 法

在建立SimMechanics仿真模型过程中有很多参数需要设置。本文先利用拉格朗日方程求得机构的逆动力学结果，将其与该机构的SimMechanics仿真结果对比，若两者一致即可验证模型的正确性。在平面机构的逆动力学中二连杆机构具有代表性，又考虑到现实使用的杆件质量分布较为分散，故以均质二连杆机构为模型进行分析。之后在正确的二连杆仿真模型基础上，建立正常步态的下肢动力学仿真模型。

1.1 利用拉格朗日方程对二连杆进行动力学求解

拉格朗日方程是对系统进行动力学分析最常见的方法之一[16]。设连杆1和连杆2的质量分别为m1和m2,对应杆长为d1和d2，重力加速度为g，本文不考虑杆的半径以及2杆之间的阻尼。为便于后文分析地面反力对下肢的影响，在该二连杆机构末端B点处施加水平方向的力Fx和竖直方向的力Fy。建立如图1所示的笛卡尔坐标系，其中z轴垂直纸面向外(图1中未标出)，θ1和θ2分别为2杆的广义坐标夹角。杆1的质心坐标为(x1,y1)，杆2的质心坐标为(x2,y2)。利用拉格朗日方程可求得杆1和杆2关节处所受的外力矩，主要计算过程如下：

1)拉格朗日函数。

L=K-P

(1)

其中，L为拉格朗日量，K为系统的总动能，P为系统的总位能。

2)拉格朗日方程。

(2)

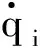
3)2杆的力矩平衡方程。

MO+FxyB+FyxB=M1

(3)

MA+Fx(yB-yA)+Fy(xB-xA)=M2

(4)

其中，(xA,yA)和(xB,yB)分别为A和B点的坐标值，MO和MA分别为O点处和A点处的合力矩。

4)系统的总动能。

(5)

其中，J1为杆1对其质心的转动惯量，v2为杆2质心的速度，J2为杆2对其质心的转动惯量。

5)系统的总位能。

(6)

其中，P取x轴为零势线。

6)将式(5)和式(6)先后代入式(1)～式(4)最终可得到连杆所受的力矩如式(7)和式(8)所示。

Fxd2cos(θ1+θ2)

(7)

Fxd2cos(θ1+θ2)

(8)

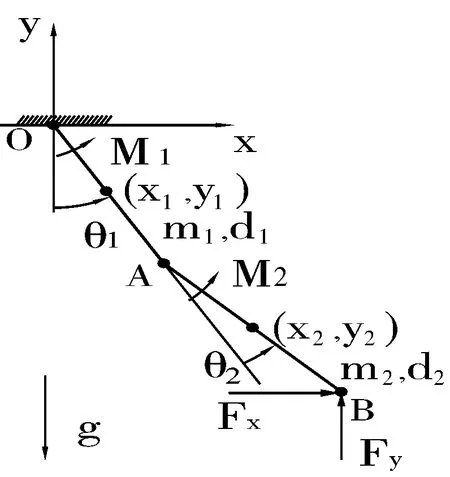
图1 二连杆机构简化图

1.2 利用SimMechanics对二连杆进行动力学仿真

根据图1，利用MATLAB中的Simulink组件按照如下步骤建立模型[17]：

1)配置机械环境参数。

设定重力参数和固定端的位置。

2)构建多体连接框图。

根据要求选定刚体的定位和约束模块，创建多体连接机构。刚体上各个特征点的位置是以θ1和θ2均为0(即2杆均与y轴重合)时进行标定的。

3)配置Actuator模块、Sensor模块以及信号的输入。

4)检查所有模块并依次连接，最终得到如图2所示模型。

5)设定模型仿真参数，主要包括模型运行的起始时间、解析器的选择等。为得到与动力学方程得出同时刻的力矩，求解器的选项中选择固定步长模式，并取步长为0.001 s。同时在可视化中勾选“在仿真显示动画”选项。

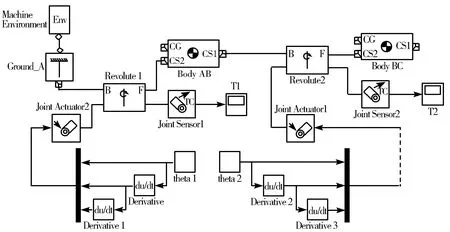
图2 二连杆机构的仿真模型

1.3 建立人体下肢的SimMechanics动力学模型

为便于分析人行走时的动态特性和合理简化模型，建模中做出以下假设：

1)下肢双侧结构完全相同，单侧为3杆机构，包括大腿、小腿和足部，以及各1个旋转自由度的髋关节、膝关节和踝关节(单侧下肢简化如图3(b)所示)。

2)下肢只在矢状面内运动，髋关节固定在平面上。

3)脚底压力作用点为脚底与地面接触区域的中心点。

4)脚底与地面不存在打滑现象。

(a) 实物图 (b) 简化图图3 正常行走时的单侧下肢

正常成年人在行走时的步态呈周期性变化，美国加州Rancho Los Amigos医学中心将一侧足跟触地到同侧足跟再次触地所经历的时间称为一个步态周期，包括支撑相和摆动相[18]。因左右肢的结构一致，故全文只分析了单肢在一个步态周期内的运动情况。

康复医学对下肢各个关节角度按照图3(b)进行定义：θ1为髋关节角度，θ2为膝关节角度，θ3为踝关节角度(其中θ1和θ2屈曲为正，θ3背屈为正)。文献[8]指出了人体下肢各体段的质量、质心位置以及回转半径(见表1)。

表1 人体下肢的运动学数据

除了姿势的改变，脚底作用力也同样影响着关节的动力学。文献[19-20]表明，因载荷刺激脚底上的皮肤受体并为康复实践提供有用的感觉反馈，脚底作用力在步行康复中起着重要的作用。在行走过程中脚底作用力分为地面的垂直压力和摩擦力，而且它们均作用在不断移动的压力点上。之后按照前面的建模方法，可以得到人体单侧下肢的SimMechanics仿真模型如图4所示。

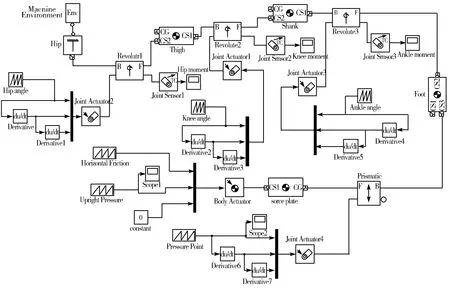
图4 正常行走时单侧下肢的仿真模型

2 实验结果

2.1 2种方法求解二连杆动力学的结果

待模型建立之后，需要给定输入以驱动系统的运转。在机器人控制中，若已知机器人的关节变量，则可根据其运动方程确定机器人的位置[21]，因此以机构关节空间的轨迹作为模型的输入。表2是二连杆机构运动的已知条件和边界条件[21]，根据上述条件对关节1和关节2分别采用3次和5次多项式进行轨迹规划，得到关节1的角度为：

θ1=30t3-5.4t2+30

(9)

关节2的角度为：

θ2=0.0464t5-0.58t4+1.6t3+2.5t2+30

(10)

表2 二连杆机构运动的已知条件和边界条件

对式(9)和式(10)分别关于时间t进行多次求导可以得到关节1和关节2的角速度和角加速度。令m1=m2=2 kg,d1=d2=0.3 m,g=9.81 kg/m2,Fx=Fy=5 N。然后通过将拉格朗日动力学方程与直接利用SimMechanics建模得到的数据编写成m文件，并在MATLAB的环境下运行该文件。为便于对比分析，将求得的结果分别除以对应连杆的质量，最终结果如图5所示。对比2种方法求得的杆1和杆2的关节力矩，结果显示：在整个运动过程中杆1的关节力矩持续增大，杆2的关节力矩在小范围内发生波动；利用动力学方程和仿真实验2种方法得到的结果完全重合，这验证了SimMechanics仿真模型参数设置的正确性。

图5 利用2种方法分别求得2杆的关节力矩

2.2 人体行走步态的动力学结果

本文以文献[20]中的一组正常行走的步态数据作为主要参考数据。为减小实验数据中噪声带来的干扰，根据人体正常步态的特点，采用傅里叶拟合对原始输入信号进行降噪处理。通过分析，采用5次傅里叶拟合效果较好，拟合结果的均方根误差均在5%以下。图6、图7(a)、图7(b)分别对应一个步态周期中各关节角度、脚底作用力、脚底压力点位移关于时间的曲线，其中图上点画线为文献[20]的实验测量数据，实线为通过MATLAB傅里叶拟合的结果。

本文进行了2组仿真，第1组是为了验证下肢模型的有效性,在模型中添加以上完整的输入信号；第2组是为了验证地面反力对步态是否有影响,在第1组的基础上令地面反力为0。

通过仿真可以得到各个关节处的力矩。为便于分析，将实验时间和脚底压力点的位移分别进行归一化处理，并将脚底作用力和求得的各关节力矩分别除以受试者的质量。图8为各关节的力矩，虚线为第1组仿真得到的结果，点画线为第2组仿真的结果，实线为实验测量的关节力矩。为方便比较仿真结果的差异性，取2条曲线交叉区域的面积与对应真实实验的曲线和横坐标轴所围面积的比值作为偏差值。通过计算得到第1组仿真的总力矩与地面行走的总力矩仅存在23%的偏差，而第1组仿真的总力矩和第2组仿真的总力矩存在89%的偏差，具体结果如表3所示。此外，2次仿真时出现的动画与人实际行走的步态也极为相似。

图6 各关节角度的对比

图7 脚底作用力和脚底压力点位移的对比

3 讨论与分析

通过二连杆机构中对比，发现2种方法得到的动力学结果相吻合，说明了该二连杆的SimMechanics模型是正确的。从中也可看出采用传统计算方法具有以下弊端：

1)计算复杂，不便检查。

2)灵活性较差，模型条件稍微变化，整个过程又要重新计算，降低了设计的效率。

采用SimMechanics建模方法恰好弥补了上述缺点，并且可以直观看到物理机构之间的位置关系。此外通过SimMechanics工具箱提供了强大的可视化功能，通过运行模型实现了机械结构运动的仿真，由此可以判断出所建的模型是否符合设计要求。

在以上二连杆系统模型的基础上，逐步完善模型，实现对下肢的动力学仿真。由于行走过程中涉及的关节运动多变以及脚底受力复杂，所以利用仿真的方法分析下肢各关节的力矩是可取的。

本文将正常行走时的实验数据导入下肢模型，进行了2组仿真。通过对比第1组仿真结果和真实实验结果，无论是单个关节力矩还是总力矩两者对应的结果均比较接近，验证了本文所建的下肢模型是有效的。之后对比第2组仿真结果和第1组仿真结果发现，单个关节力矩和总力矩的差异均较大，说明地面反力对髋、膝、踝关节力矩影响都很大。此外，从第2组仿真结果发现膝关节力矩和踝关节力矩在整个步态周期中趋近于0，而髋关节力矩仍沿着第1组仿真结果的趋势进行变化。由此推断膝关节力矩和踝关节力矩主要受地面反力的影响，而髋关节力矩受地面反力的影响但不是主要影响。以上表明地面反力在行走步态中不应被忽略，并且还起着重要作用，这为步态康复训练提供了有效的指导意见。

4 结束语

本文先通过建立正确的二连杆机构的SimMechanics动力学仿真模型，然后在此基础上依据人体下肢的结构参数建立了单侧下肢的仿真模型，并以各关节角度、脚底作用力作为输入，关节力矩作为输出进行了逆动力学仿真分析。通过2组仿真实验对比得出地面反力对步态起着重要作用，这为步态康复训练提供了良好的指导作用。同时该下肢动力学模型的正确建立为研究人体步态运动提供了有效的方法。