FFT计算菲涅尔衍射相位的跳变与矫正研究

向红丽,范 琦,李 云,王云飞

(1.西安邮电大学研究生院,陕西 西安 710061; 2.空军工程大学理学院，陕西 西安 710051;3.西安邮电大学理学院,陕西 西安 710061)

0 引 言

随着阵列型探测器制作工艺及计算机技术的进步，数字光学和计算光学在生产中得到了广泛的应用，如数字全息[1-3]、光学图像加密[4-6]、数字波面干涉[7-8]、相位解包裹[9-10]及波面重建[11-12]等，在这些应用中衍射相位的计算具有重要作用[1,4-5,8-11]，其计算结果的精度直接影响了后续的计算精度。菲涅尔衍射作为标量衍射理论中重要的组成部分，是应用最广泛的衍射分析方法。笔者研究发现当采用傅里叶变换算法计算相位时，在相位未解包裹的情况下，接收面上提取的相位分布曲线会出现跳变，如果进行解包裹，必然会导致错误的结果。本文对傅里叶变换算法计算菲涅尔衍射的相位跳变原因进行分析，提出2次倒谱的矫正方法，并对二维矩孔的菲涅尔衍射情况进行仿真研究。

1 理论分析

1.1 傅里叶变换的快速计算机实现

一维傅里叶变换[13-15]的定义：

其中，I{ }代表对{}中的内容进行傅里叶变换，F(u)和f(x)是一对傅里叶变换对，u和x分别是频域和空域变量。因为在计算机中进行数值计算时，函数会表示为向量或矩阵这样的离散形式，所以在计算机上实现傅里叶变换，也要先将上面的傅里叶积分离散化为：

(1)

其中，fn是连续函数f(x)经采样以后的离散化表示，Δx是空域的采样间隔，n是采样的索引。假如继续对频域坐标u在区间[0,1/Δx]内以频率1/(MΔx)进行采样，那频域坐标可表示为：

其中，M是频域的采样数，m是频域的采样索引。将u代入式(1)得：

(2)

为了直观，将m、n替换为更为常用的频域索引u和空域索引x，此时x将变成自然数，Δx变为1，于是式(2)就变为:

(3)

式(3)就是一维快速傅里叶变换(FFT)的表达式，是离散傅里叶变换(Discrete Fourier Transform, DFT)的一种快速算法。

仔细考察式(1)和式(3)，容易发现自变量的取值范围发生了变化，式(1)中坐标取值是关于原点对称的，而式(3)仅在非负半轴取值。

1.2 由坐标索引引起的相位偏移

图1 目标矩阵示意图

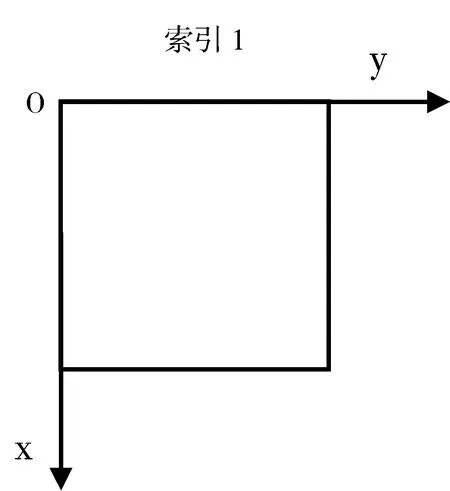
图2 矩阵索引示意图

为了分析FFT对计算结果相位的影响，对图1所示的11×11二维矩阵做2种索引中的DFT。图1中黑色方块代表0，白色方块代表1。2种索引的区别在于：第1种索引将原点设置在矩阵的左上角；第2种索引方法将原点设置在矩阵中心(如图2所示)，为了简便，分别称之为索引1和索引2。事实上索引1正是计算机中FFT所用的索引标记方法。而索引2则是在模拟信息光学的计算中坐标系的取法。在垂直于光轴的截面上，以光轴所在点为坐标原点，光学元件相对于光轴以中心对称的方式排列。

在2种坐标系下，DFT的表达式分别如式(4)和式(5)：

(4)

(5)

为模拟FFT的计算过程，利用式(4)进行编程，得到的结果如图3所示的FFT相位分布。从图3可以看出，由于索引及傅里叶变换对称性的原因，零频分量被分配在了视野的4个角上。

图3 索引1变换结果

图4 索引2变换结果

为了比较，再利用式(5)编程计算DFT，得到如图4所示的结果。对比图3和图4中的结果可以看出，二者的相位分布有较大差异，主要表现在：1)索引1中的相位起伏较大，变化剧烈，索引2中的相位变化相对平缓；2)索引1中的相位沿着y=x这条直线变化，并以这条直线对称，索引2中的相位则由图片中心向四周变化，呈中心对称的形状。

从以上讨论可以看出，由于FFT算法对矩阵的索引方式与菲涅尔衍射公式不同，导致FFT算法得到的相位与在对称索引下得到的结果产生了很大差异，因此如果直接用FFT进行衍射计算，很有可能会对计算结果的相位造成影响。

1.3 对FFT的矫正

为了矫正这种误差，需要对传统的FFT使用方法做一些改进。考虑到FFT对计算结果相位的影响，是由FFT对矩阵的索引标注方式引起的，这种索引相当于将矩阵平移了半个周期。为了矫正这一平移对计算结果的影响，可以在用FFT对矩阵进行傅里叶变换之前，先对目标矩阵做一次倒谱变换。

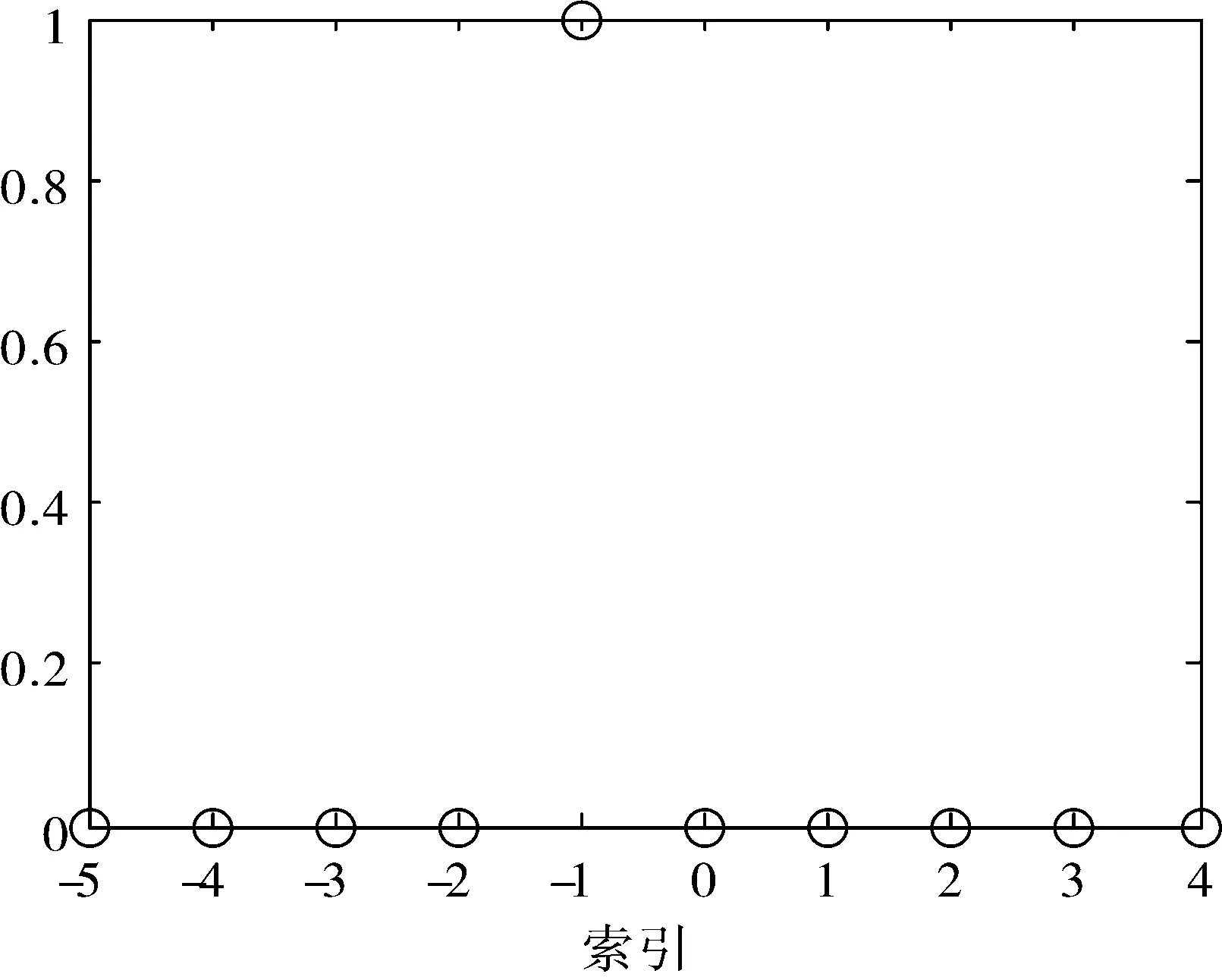
图5 目标函数

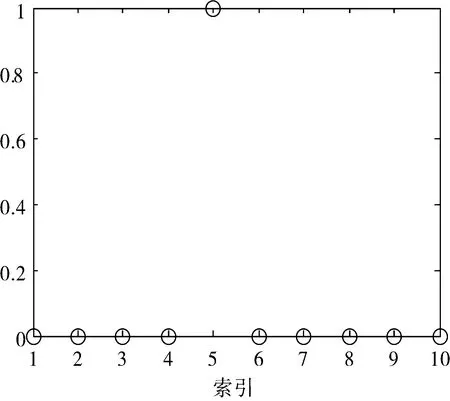
(a) 计算机默认数组

(b) 一次倒谱后数组图6 倒谱变换前后的结果

为简单直观，以一维数组[0 0 0 0 1 0 0 0 0 0]为例，假设其是如图5定义的函数，但在计算机中，默认的数组索引如图6(a)所示。对数组做倒谱变换，实质上是将数组的左半部分与右半部分交换了位置。对图6(a)中的数组做倒谱变换，得到如图6(b)所示的数组，将其与图5中的数组相比较，如果将图5中的函数看做一个以10为周期的无限长周期函数的一个周期，那么两者可看做同一周期函数在不同位置上分别取样一个周期所得的结果，根据周期函数的性质，两者的傅里叶变换结果应该是一样的。

本文对图6(b)中的函数进行FFT计算，得到如图7(a)所示的相位分布，考虑到观察的方便，接下来还要对其再做一次倒谱变换，这样便得到如图7(b)所示结果，为了方便比较，本文同时将图5所示函数通过解析计算的相位以圆圈的形式绘于其中。

从图7(b)中可以看到2种方法得到的相位，除了在第一个点外其他点均符合得很好。此外，2种方法在第一个点得到的相位正好相差2π(一个周期)，可以认为通过在对矩阵做FFT前后实施2次倒谱变换，可以矫正FFT对计算结果相位带来的误差。

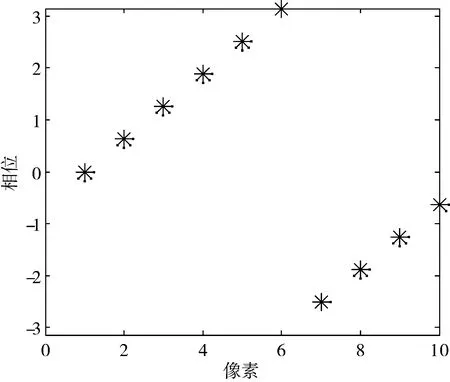
(a) 一次倒谱后相位谱

(b) 2次倒谱后相位谱图7 对FFT进行矫正后的结果

2 仿真实验

接下来进行二维衍射仿真实验，这里仅讨论方孔的菲涅尔衍射情况。矩孔衍射面如图8所示。构造方孔仿真菲涅尔衍射，入射光为波长λ=632.8 nm的单色平行光，衍射屏宽度x0=y0=2.5 mm，衍射面和观察面采样点数512×512，中心方孔采样数70×70，衍射距离z=6.5 mm，编写程序利用Matlab进行计算。

图8 矩孔衍射面

编程实现单次FFT的矩孔菲涅尔衍射，观察面上相位分布如图9所示，放大会看到受FFT数据处理方式的影响，中心区域会出现黑白相间的色块，这是矩孔进行FFT运算后在观察面中心区域出现剧烈的相位变化，在计算出的相位未解包裹的情况下，中心区域表现出的明显的相位跳变，提取相位图中心一行的相位数据，在图9中用白色线段标注，画出相位曲线如图10所示。

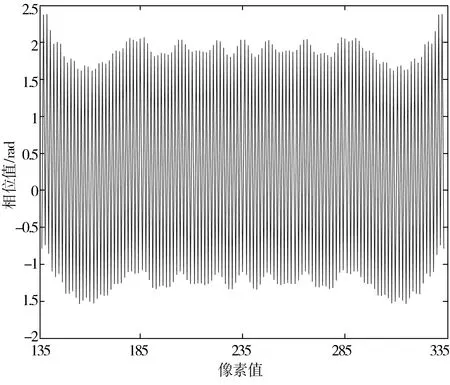
图10 相位分布中心一行的相位曲线

从图10可以看出，在衍射面中心区域的相位分布存在着剧烈跳变，如果进行解包裹，必然会导致错误的结果，因此有必要进行矫正。

在对式(4)进行FFT运算前，对衍射面倒谱，即进行fftshift操作，并在FFT运算后也进行一次倒谱，得到相位分布如图11所示。

图11 矫正后衍射相位分布图样

2次倒谱对相位的影响在图11中宏观上表现得不明显，作为比较同时画出矫正前后相位分布中心一行的相位曲线，如图12所示。

图12 矫正前后衍射相位分布

从图12可以看出，矫正后在观察面中心区域的相位曲线没有出现跳变，并将矫正前跳变的相位曲线沿底部包裹住，展示了衍射观察面上正常的相位分布，这表明在利用单次FFT进行菲涅尔衍射相位的计算时，通过对衍射面上离散化数据整体在FFT计算前后分别进行一次倒谱操作，即可避免由FFT算法引起的观察面上相位分布的跳变。

3 结束语

本文研究了菲涅尔衍射积分的傅里叶变换算法。通过分析发现FFT算法对离散化平面进行运算时，由于计算原点选取在平面的左上边角顶点，而离散傅里叶变换和实际衍射是以衍射面几何中心作为计算原点，这导致在衍射的计算过程中，FFT算法相当于对衍射平面在空间进行了平移。根据傅里叶变换位移定理，这种空间位移使相位分布在观察面上出现大幅度变化，在未解包裹的情况下就会出现相位值在0～2 pi范围内的连续跳变。为解决这种相位跳变问题，本文提出在FFT运算前后分别进行一次倒谱的方法，并运用单次FFT对二维矩孔的菲涅尔衍射进行仿真，用2次倒谱矫正了接收面上的相位跳变，仿真结果证明了该矫正方法的可行性。