基于VLBI与BDS联合解算ERP的算法研究

刘聪,孟鹏飞,刘鑫

(1.上海勘察设计研究院(集团)有限公司,上海 200438； 2.中国矿业大学 环境与测绘学院,北京 100083)

0 引 言

高精度的地球自转参数(ERP)在人造卫星和深空探测卫星的定位和导航,地球参考框架的建立与维持等方面有着广泛的应用[1]。20世纪70年代以来,随着甚长基线干涉测量、激光测卫、全球卫星导航系统等空间技术的快速发展,在确定地球自转参数精度上有了量级的提高。这些空间测量技术均能够测定全部或者部分高精度的地球定向参数(EOP)[2]。中国自主研发的全球卫星导航与定位系统:北斗卫星导航系统(BDS),是全球四大卫星导航系统(GPS、GLONASS、BDS、GALILEO)之一,现已覆盖亚洲区域,预计2020年左右将覆盖全球[3-4]。北斗卫星导航系统对于我国国防以及国家经济建设有着不可估量的价值。为提高北斗卫星导航系统在参考框架的建立与维持、导航定位、通信等各方面服务的能力,国内学者进行了大量的研究工作[5]。杨元喜等人从用户角度对亚太地区的北斗卫星导航系统的导航与定位能力进行了初步的研究与评估[6];马宏阳等人进行了北斗卫星导航系统解算地球自转参数以及对流层延迟的研究;魏二虎等人进行了近三年VLBI解算地球自转参数的研究。已有结果表明了目前BDS技术能够提供较高精度的地球自转参数序列值,但是稳定性有待提高,而甚长基线干涉测量观测数据解算ERP的优势在于精度高、稳定性强,但其缺点在于测站较少且观测不连续。联合BDS和VLBI技术解算地球自转参数能够利用各自的优势,有望解算出连续稳定的ERP参数序列,为我国独立自主解算地球自转参数提供有益参考,同时对于我国守时、授时、导航与定位、人造卫星精密测定轨和深空探测等科研工作都具有重要意义[7]。

1 BDS与VLBI解算ERP的原理

1.1 BDS估计ERP的基本原理

在解算工作中,BDS的载波相位为观测量,维护ITRF2005框架的站坐标和卫星轨道参数来自IGMAS,解算量是站坐标、卫星坐标、地球自转参数和大气延迟参数。

其中北斗载波相位观测值表示为待估参数的函数模型为

L=M(t,Xerp,Xatm,Xn,Xt,Xsp)+ε,

(1)

式中:M为BDS观测量与解算参数对应的函数模型;t为时间;Xerp为地球自转参数;Xatm为大气延迟;Xn为相位模糊度;Xt为IGMAS测站的坐标;Xsp为初始时刻的轨道根数和摄动参数;ε为观测噪声。

将式(1)线性化后,地球自转参数的偏导数为:

(2)

式中:r和R1分别为卫星和测站在惯性坐标系的位置矢量[5];ρ为站星距; ∂R1/∂Xerp包括极移在x和y方向的分量及UT1-UTC的一阶变化率:

(3)

(4)

(5)

式(5)中,

(6)

(7)

由于GNSS技术中轨道与UT1-UTC参数具有强相关性,无法独立解算UT1-UTC的绝对量,只能解算UT1-UTC的相对变化量。故本次实验对先验UT1-UTC(IERS下载)参数赋予10 μs的强约束,然后通过公式(UT1-UTC)t=(UT1-UTC)t0+d(UT1-UTC)t-t0,达到间接“估计”UT1-UTC的目的。其中,d(UT1-UTC)t-t0为t0到t时刻UT1-UTC的变化量。

1.2 VLBI解算ERP的基本原理[1,8]

VieVS软件采用最小二乘平差进行VLBI大地测量的参数解算,流程图如图1所示。设VLBI的基本观测方程为

Δτj+ΔC0i+ΔC1i(tj-t0) ,

(8)

式中:RZ(θj)、RY(ξj)、RX(ηj)为自转矩阵和极移旋转矩阵;t0为起始观测历元;tj为观测的历元;Bj为准惯性坐标系中的基线矢量;Sj为观测源方向; ΔC1i为钟速;c为光速; Δτj为延迟改正; ΔC0i为钟差。

在进行解算地球自转参数时,将射电源位置和基线坐标等参数设为已知,可得到误差方程式:

Vj=A·dx+ej

(9)

式中:A为改正数的偏导系数矩阵;dx为ERP改正数;ej为方程常数项。最后,可根据经典最小二乘理论估计ERP参数值。

2 数据处理

2.1 BDS数据处理及分析

本次实验选取国际GNSS检测评估系统(iGMAS)中国矿业大学北斗分析中心提供的2016年61-91天的数据,为了获得较好的精度,选取了全球均匀分布、几何结构良好、相对稳定的北斗观测站进行解算,所选测站分布图如图2所示。将最终得到的ERP与IGS发布的最终地球自转参数作比较,采用差值绝对值的均方根来评定外符合精度,其差值统计信息如图3和表1所示。

表1 地球自转参数偏差统计

BDS解算值与IGS结果做差的均方根如表1所示,极移在X方向上的RMS为1.76 mas,在Y方向上的RMS为3.19 mas,UT1-UTC为0.15 ms.表明目前北斗系统解算地球自转参数可以达到较高的精度。由图3可以看出由于所选测站在全球均匀分布,BDS解算地球自转参数无明显系统偏差,极移参数解基本与IGS发布值相符合,但是在第74-76天和第84-85天出现了较大的残差,说明利用北斗卫星导航系统解算ERP稳定性有待提高[9]。

2.2 VLBI数据处理及分析

本文用VieVS2.2软件处理与BDS同时段的NGS格式的VLBI数据。在进行解算地球自转参数时,大部分参数和模型选择默认值[10-11],详见文献[9-10]。由于VLBI观测数据是不连续的,在进行数据联合解算时需要对VLBI解算的ERP结果进行插值方可进行组合解算。故首先利用分段三次Hermit插值方法对不连续的ERP插值到每天UTC 00:00:00[12],并将VLBI的插值前后的ERP结果与IERS发布的EOP08 C04序列结果进行做差比较,用差值绝度值的均方根来评定外符合精度。其偏差统计如图4和表2所示。

统计项RMS(插值前)差值平均值RMS(插值后)差值平均值 X方向0.217 mas0.161 mas0.274 mas0.214 masY方向0.235 mas0.208 mas0.270 mas0.228 masUT1-UTC/ms0.0190.0120.048 mas0.033 mas

图4中可以看出,除了UT1-UTC的插值在儒略日57458-57460出现较大跳变,其它插值结果都较为平稳,在合理范围之内。从表2中插值前后的RMS值可以看出,虽然VLBI解算极移和UT1-UTC参数在插值后精度有所下降,但RMS值均在一个量级,说明插值结果是可靠的。

2.3 基于IERS 08C04序列的加权平均

由于BDS解算的ERP结果的时刻是UTC 12:00:00,为与同时刻VLBI解算结果联合,故首先要获得每天UTC 00:00:00的参数值,同样采用Hermit插值方法进行插值,然后计算与IERS 08C04序列相比较的均方根,最后以BDS和VLBI的均方根的平方的倒数作为权进行加权平均,相关公式如下:

(10)

(11)

ERPVLBI+BDS=

(12)

RMSVLBI+BDS=

(13)

式中:ERPBDS、ERPVLBI、ERPVLBI+BDS分别为利用BDS和缺失结果补偿后的VLBI序列以及加权平均后的ERP序列,RMSVLBI、RMSBDS、RMSVLBI+BDS分别表示以上序列与ERPIERS比较差值的均方根。联合计算结果及差值统计如图5和表3所示。

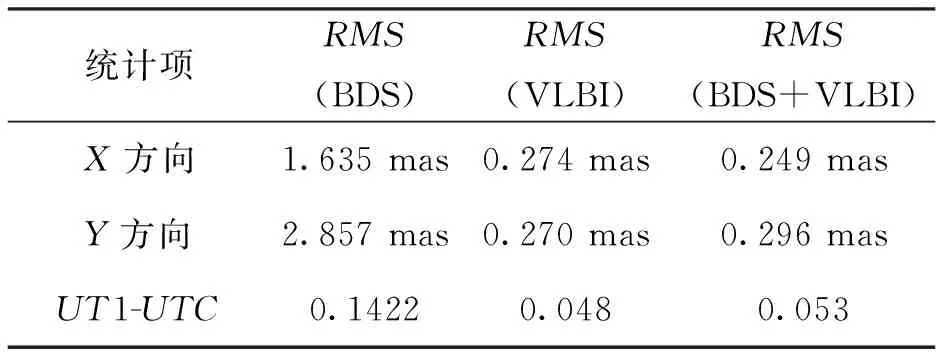
统计项RMS(BDS)RMS(VLBI)RMS(BDS+VLBI) X方向1.635 mas0.274 mas0.249 masY方向2.857 mas0.270 mas0.296 masUT1-UTC0.14220.0480.053

从图5中可以看出,BDS与VLBI加权平均后的均方根十分靠近VLBI,这是由于VLBI解算结果精度高,所占权重大的缘故。从表3的统计数据可以看出,经过加权平均后,极移在X方向上的精度比联合前都要好些;极移Y方向和UT1-UTC的精度位于BDS和VLBI单独解算结果之间,比较靠近VLBI插值后的解算精度,这是由于BDS解算精度相对VLBI低很多,所占权重小的缘故。总的来说,加入VLBI数据对于BDS数据来说稳定性、可靠性均有很大的提高。

3 结束语

采用基于IERS 08C04序列的定权方法对BDS和VLBI数据解算ERP结果进行加权平均以求得ERP的组合解。实例表明了北斗与VIBL相结合能够有效地提高北斗ERP的解算稳定性和精度,验证了本文提出组合北斗以及VIBL方法的可行性。由于VIBL数据密度小,本文采用分段三次Hermit插值将VLBI插值到与IERS相同历元,同样将BDS数据插值到与IERS 08C04相同历元,并基于IERS 08C04数据计算各自的均方根,并依据均方根的平方的倒数作为权进行加权平均。将BDS和VLBI数据解算结果进行加权平均综合后,精度相比BDS数据稳定性和可靠性均有所提高。

致谢：国际GNSS检测评估系统(iGMAS)和IVS以及IERS 为本文提供的数据产品。