K-means++分区法在密集型测站中的应用研究
郝美云,孙宪坤,丁倩云,尹玲,尹京苑
(1.上海工程技术大学,电子电气工程学院,上海 200000; 2.上海市地震局,上海 200000)
0 引 言
利用GAMIT软件处理大型密集的测站时由于软件自身处理测站数的能力限制,只能同时处理少于100个测站的数据,所以需要对测站进行分区处理[1]。目前国内采用的经纬度分区和区域板块分区方法会导致长短基线同时存在。对于中长基线的解算,GAMIT软件可以达到很高的精度,而对于短基线其解算精度则相对较低[2]。所以当长短基线同时存在时,由于采用了相同的模型就会降低整网解算精度。针对这个问题,不少学者进行过相关研究。李兵等[2]为提高分布密集型测区的基线解算精度,提出了一种新的分区处理方案——“间距分区法”。该方法可以有效地避免短基线的存在,解决GAMIT 数据处理过程中短基线解算精度较低的问题,在区域网基线解算中能够有效地提高基线解算精度。万军等[3]提出了格网间距分区的方法来避免较短基线的存在,提高了整个测区的解算精度。随后曹炳强[4]等又验证了间距分区法在针对解算数量多、分布密集测站时的精度可靠性。
虽然间距分区法能从一定程度解决长短基线带来的低精度问题,但实际操作需要人为在地图上找出测站分布并计算各个测站之间的距离,再将分布密集的测站抽稀[2],这是一项繁琐耗时的工作。基于此,本文引入了K-means++算法思想来实现大型密集测站分区。利用K-means++算法对测站进行聚类,再利用Hash算法进行排序组合,形成均匀分布的子网。实验中采用整网解算结果作为标准值,分析区域分区法和K-means++分区法的基线长度、基线精度及三维坐标差,然后再将K-means++分区方法与间距分区法进行实验对比分析。实验结果表明K-means++分区方法比一般区域分区法具有更高的解算精度,可以将测区站点最大程度均匀分布从而减少长短基线差异大的现象,并且与现有的间距分区法具有同样高的解算精度。
1 K-means++算法
辜声峰等[5]在探讨大规模基准站组网与分区服务技术的时候引入了FCM算法进行子CORS三角网的分区。与 K-means++算法相似,FCM算法也是一种典型的聚类算法。不同的是,K-means是排他性聚类算法,即一个数据点只能属于一个类别,而FCM只计算数据点与各个类别的相似度。K-means++算法在一定程度了解决了K-means算法只能达到局部最优的问题,其核心思想是把n个数据对象划分为k个聚类,使每个聚类中的数据点到该聚类中心的平方和最小[6]。算法流程如图1所示。
假定训练样本为{x(1),x(2),…x(m)},x(m)∈R,对于每一个样例i,根据式(1)计算其所属类别。
(1)
式中:C(i)为样例i到所有初始聚类中心的最小距离,其对应的聚类中心就是该样例所属的类别;uj代表初始的k个聚类中心。计算出每一个样本所属类别后,所有样本被分成了k个类。根据公式(2)重新计算每个类的质心。质心是指一个类簇内部所有样本点的均值。
(2)
以式(2)为例,计算类别j中的所有样本x(j)到聚类中心uj之间的距离均值。重复上述步骤,直到质心不变或者变化很小。这个收敛条件定义一个畸变函数来表示
(3)
式中:uc(j)为每个样本点对应的聚类中心;J函数为每个样本点到其质心的距离平方和,K-means++算法就是要将J值调到最小。
2 改进的K-means++算法分区方案
针对目前的区域分区方法导致的长短基线同时存在而使解算结果精度降低的问题,文中引入K-means++算法实现聚类,再利用Hash算法进行排序分组来实现分区,称此分区方案为改进的K-means++算法分区方案,简称K-means++分区法。Hash算法,又称散列算法,能将任意长度的输入数据通过散列函数变成固定长度的输出,能够快速地将具有相同特征的数据映射到同一区域[6]。文中用到的样本数据来源于IGS数据中心,全球现在大概有400多个IGS跟踪站[8],其站点分布如图2所示。从图中可以看出15°W~60°E以及30°N~60°N围成的区域是IGS跟踪站分布十分密集的区域,包含96个密集分布的跟踪站,如图3所示。如果将该区域的所有站点进行解算,必然会因为短基线的存在而使整网解算精度降低。本文针对这部分IGS站分布密集区域采用K-means++分区法将密集测站分为4个分区,具体算法流程如图4所示。
经过K-means++算法聚类和Hash算法排序组合能得到4个均匀分布的子网,每个子网里包含24个IGS跟踪站,如图5所示。与图3对比,分布密集的96个测站经过改进的K-means++算法分区之后,形成了四个均匀分布的子网且满足子网划分的原则[9]。每个子网各测站之间分布较为稀松,大大减少了短基线的存在。
3 实例对比分析
3.1 实验方案设计及数据处理策略
为了研究K-means++分区方法是否能够有效地解决长短基线同时存在而使整网解算精度降低的问题,文中设计了三个实验方案进行对比分析。
1) 整网解算方案:保证测站点的整体性,对其整网进行GAMIT解算和GLOBK网平差处理。
2) K-means++分区法:依据上述分区流程,将测站均匀分成四个分区,每个分区用GAMIT解算之后再联合平差处理。
3) 区域分区法:根据测站分布的空间位置和距离远近进行一般区域分区,如图6所示。对比图5,区域分区法的四个分区明显存在短基线密集的现象。上述方案中,选取一致的公共站,采取一致的处理策略。所以方案2)、3)的区别仅在于子网划分不同。因此,可以认为此时方案2)、3)之间的结果差异是由于不同的分区方案引起的。
为了确保实验结果的可靠性,用TEQC软件对96个IGS跟踪站进行质量校核,剔除了16个不可用的站,按照公共站的选取原则[10-11]选取了6个公共站,剩下的74个IGS跟踪站作为待解算站。为获取高精度的平差结果,联合2017-10-01至2017-10-03日3天的观测数据进行精密星历解算及网平差[11]。利用GAMIT10.6解算的主要参数及GLOBK网平差参数配置如下:采用RELAX解算处理模式,联合全球h文件平差处理,加固体潮和海潮改正模型。观测值模型选用LC-AUTCLN[13],天顶延迟参数个数为13,对参考站坐标X、Y、Z方向的约束为1 cm[13].采用BERE光压模型,J2000惯性系,ITRF08框架。
3.2 实验结果对比分析
按照以上方案利用GAMIT/GLOBK软件进行解算[15],统计两种分区方案解得的基线长、基线精度以及测站坐标。以整网解算结果作为标准值,分析K-means++分区方案与一般区域分区方案的基线长度、基线精度及三维方向坐标差绝对值,如图7所示。
从图中可以看出,在0~600 km短基线区间内,K-means++分区方案的基线个数明显少于区域子网划分方案;当基线长度大于800 km时,K-means++分区方案测区内的基线个数又多于区域子网划分方案的个数。说明K-means++分区方案使得测站间距保持在相对较长的水平,基线长度比较一致,有效避免了较短基线的存在。从图中可以看出,K-means++分区方案解算的测站坐标更加接近于整网解算方案,在X方向和Z方向的精度明显优于区域分区法,除个别测站外精度达到1.5 mm;在Y方向优势不明显但整体还是优于区域划分法且更加均匀、稳定,两种方案精度均优于1.8 mm.
基线基线长度/km基线精度/mm K-means++分区区域分区相对精度(10-8) K-means++分区区域分区 VILL-YEBE73.7006.446.158.738.34 HUEG-ZIM2106.8522.983.032.792.84 GANP-PENC158.4762.932.971.851.87 JOZE-LAMA201.2383.213.371.601.67 AJAC-GRAS252.7493.663.761.451.49 AJAC-GENO277.1272.933.051.061.10 BZRG-GENO298.4824.054.151.361.39 BOGI-WROC313.1185.796.041.851.93 AJAC-MARS317.4065.015.181.581.63 AJAC-PADO462.0704.254.340.920.94
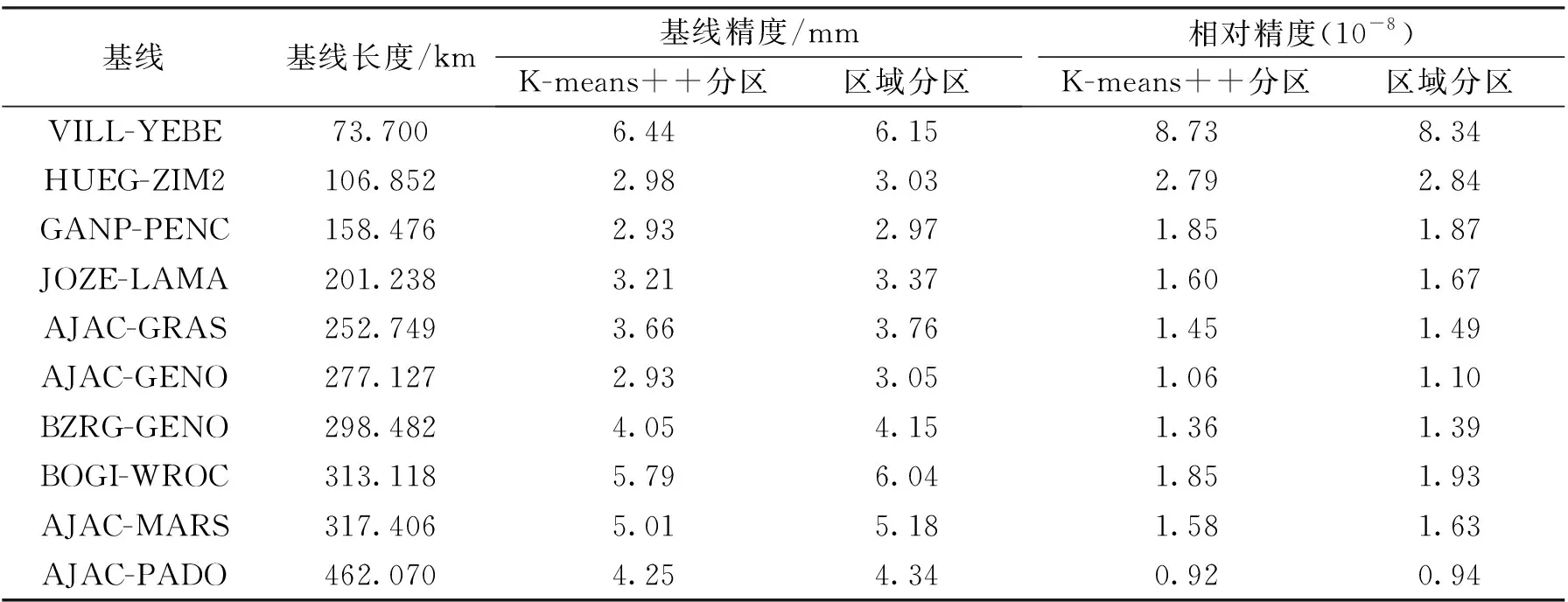
由于实验中采用的待解算的IGS跟踪站数据质量高、稳定性强[8],所以除了区域分区方案中的个别站点外,两种方案在X,Y方向上都取得了较高的精度。但对比分析图7,可以发现K-means++分区法比一般区域分区法精度更高且更稳定。为了进一步对比两种分区方案的优劣,本文统计了两种分区方案相同基线的精度和相对精度,如表1所示。分析表1可知,当基线小于100 km时,两种分区法得到的基线精度都不是很高,但K-means++分区法还是比区域分区法高0.3 mm的精度。这是因为GAMIT软件无论采用哪种分区方案,对于短基线的处理精度都较低[2]。当基线长度大于100 km时,两种分区方法的基线精度相差不大,但从表中可以发现K-means++分区比区域分区精度整体更高,且更稳定。根据实验结果可以推论,在观测数据质量良好的情况下,将K-means++分区法运用于测站分布密集的CORS站可以获得更高精度的解算结果。
4 K-means++分区与间距分区方案对比
目前为了解决长短基线同时存在而使整网解算精度降低的问题,不少学者提出了间距分区法。为了进一步验证K-means++算法的优势,利用相同的测站数据和解算处理策略,按照间距分区法的原理[4]进行分区实验。同样以整网解算结果为标准值,统计间距分区法在不同区间内的基线个数以及三维方向坐标差绝对值。图8示出了间距分区法和K-means++分区法在4个区间内的基线个数,图8(b,c,d)为间距分区法及K-means++分区法在三维方向的坐标差。
从图8可以看出,在0~600 km短基线区间内,K-means++分区法的基线个数与间距分区法的基线个数相当,短基线个数都较少;当基线长度大于800 km时,K-means++分区方案测区内的基线个数略多于间距分区法的基线个数。这说明K-means++分区方案和间距分区法都使得测站间距保持在相对较长的水平,从而有效避免了较短基线的存在。从图8可以看出,K-means++分区方案解算的测站坐标在X、Y、Z方向的坐标差与间距分区法的X、Y、Z方向坐标基本相差不太,但K-means++分区法坐标差整体稳定一点。除个别站点外,两种方案的三维方向坐标精度均优于1.8 mm.这说明K-means++分区方案与间距分区法都能解决长短基线同时存在而使整网解算精度降低的问题,前者精度更加均匀稳定一些。并且K-means++分区法避免了繁琐的人工计算和数据处理步骤,在保证精度的前提下更加高效。
5 结束语
GAMIT/GLOBK软件依据双差原理进行数据解算,短基线之间相关性很大,长基线相关性不大,从而导致对长短基线解算策略存在差异[3]。当长短基线同时存在时,由于采用相同的模型而导致整网解算精度降低。对此,引入了K-means++算法结合Hash算法进行分区。采用整网解算方案作为标准值,分别解算区域分区方案、K-means++分区方案及间距分区方案,统计三种分区方案的长短基线个数及三维坐标差。实验结果表明,K-means++分区法比一般区域分区法具有提高解算精度的优势;与间距分区法相比,具有一定的稳定性和高效性。

