模糊逻辑控制的车辆稳定系统动力学仿真
郝正君,杨柳青
(1.河南警察学院 交通管理工程系,郑州 450046; 2.安徽理工大学 机械工程学院,安徽 淮南 232001)
车辆稳定控制系统是一种主动安全控制系统,是现代汽车控制系统领域研究的热点,广泛应用于国内外许多高级轿车[1].在车辆稳定控制研究的最初阶段,各个生产厂家对稳定控制定义了很多名称,如车辆动力学稳定性控制、车辆电子稳定程序控制、车辆稳定性控制等[2],但是其功能大体相同,本文统一定义为车辆稳定性控制系统.随着路面状况的不断变化,车辆稳定性控制理论研究也在逐渐的深入,出现了车辆横向摆动控制概念,通过分配车轮的驱动力或制动力来调节车辆的横向摆动,从而保证车辆行驶的稳定性.
车辆在复杂路况状态下行驶时,其稳定性控制非常重要.当前,研究者对车辆行驶稳定控制方法进行大量研究.例如:文献[3]提出了车辆直接横摆力矩和前轮主动转向控制方法,建立车辆非线性模型,采用侧偏角速度确定车辆稳定区域,对于稳定区域之外采用直接横摆力矩和前轮主动转向控制,使侧偏角和横摆角速度接近理想值;文献[4]提出了车辆稳定性的滑模变结构控制方法,创建了车辆稳定性参考模型,根据滑模控制原理设计了控制系统上层控制器,确定了车轮制动时的分配策略,提高了车辆主动安全性;文献[5]提出了两级分层车辆稳定性控制系统,上层控制器控制车辆的横摆运动,下层控制器控制车轮滑移率,从而控制车轮的制动力矩,有效地改善了车辆稳定性控制系统,控制效果较好.但是,以往研究的车辆稳定系统在受到路面复杂路况干扰时,车辆抖动程度较大,有可能发生侧翻现象.对此,本文以8自由度车辆简图为研究对象,建立其侧倾载荷传递模型,分析了模糊控制结构,推导出车辆侧倾运动控制方程式,定义模糊隶属函数,采用模糊逻辑控制设计车辆侧倾控制系统.将车辆控制参数输入Matlab软件中进行动力学仿真,并与PID控制系统仿真结果进行比较,为深入研究车辆行使稳定性控制系统提供了理论依据.
1 车辆模型
1.1 8自由度车辆模型
采用非线性8自由度车辆模型,通过侧倾试验模拟车辆的控制,如图1显示.该模型相关的自由度包括纵向速度u,横向速度v,横摆角速度r,侧倾角φ,四轮的转速ωfl,ωfr,ωrl和ωrr.由牛顿-欧拉公式可知,8自由度车辆模型非线性运动方程为[6]
式中:ms为车辆簧载质量;Ixx,Iyy,Izz分别为绕x,y,z轴的转动惯量;Ixz为与x轴和z轴的惯量积;Fx,Fy分别为x轴和y轴的合力;Mx,Mz分别为绕x轴和z轴的转矩;hs为簧载质量重心与滚动中心的距离;g为重力加速度;Kφ和Cφ为阻尼系数.
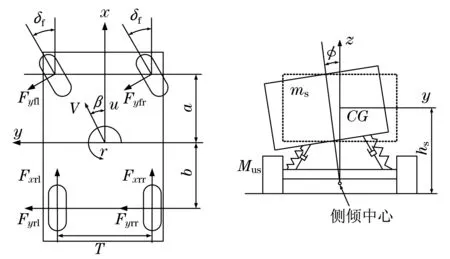
图1 8自由度车辆模型Fig.1 Eight degree of freedom vehicle model
1.2 车辆侧倾模型
为了评价车辆在重型机动情况下的侧倾性能,应考虑影响车辆侧倾稳定性的主要参数:重心、车辆轨道、轮胎和悬架性能的变化,如图2所示.

图2 车辆载荷传递图Fig.2 Vehicle load transfer diagram
通过在y轴方向上建立牛顿第二运动定律及绕z轴和x轴方向建立力矩平衡,可以分别表示横向、偏离和侧倾的运动方程[6]为
式中:ay为侧向加速度;Fyf,Fyr分别为前后轮胎侧向力;δ为轮胎转角;Iz和Ix为车辆侧倾的转动惯量.
1.3 荷载传递
若车身侧倾,前、后轴的左右车轮将在一侧增加载荷,另一侧则相应减小.这就是所谓的由侧倾导致的负荷转移.定义车辆的负荷转移为轴载ΔF,在侧倾中心的滚转力矩垂直于汽车纵向平面的车轮并处于平衡状态,如图2所示,可推导出如下方程[7]:
(12)
侧翻性能初等级可仅从车辆静态稳定系数Fss求得确定.车辆的Fss是基于其最重要的几何性质计算得出的侧倾阻力值.车辆的Fss计算以外部轮胎产量接触中心矩为依据:
(15)
Fss数值越小,车辆在单车倾斜碰撞中更容易侧翻;较高的Fss值可以保证车辆更好的稳定性和平衡性.
2 控制器设计
在本文中,开发了一种基于模糊逻辑控制器的非线性车辆模型,为防止侧倾角增大通过控制器导出的前转向角和动量值被定义为系统输入值.状态变量包括横向速度、横摆角速度、侧倾角和侧倾角速度:
(16)
在考虑8自由度车辆模型的基础上,将控制器设计的状态空间描述[8]为
(17)
研究的主要目的是为了减少侧倾角或增加侧翻临界值(稳定性),因此,控制器应调整其横向载荷传递转移值TLL处于其最佳条件.TLL标准值是关于横向加速度、侧倾角度及侧倾角速度的函数,可通过如下方程[9]求得:
(18)
当一个轮胎失去了与路面的抓地力,地面在轮胎上的作用力会消除,会导致侧翻的发生.在此情况下侧翻发生时TLL的值变成1.当两侧轮胎上的力相等,TLL值为0,此时车辆处于最稳定的状态.
2.1 最优控制
根据最优控制理论,基于侧倾角的函数应尽量减少为[10]
(19)
式中:Xd=[ydvdφdrd]T为期望的状态变量;Q为一个半正定状态加权矩阵;R为由试验和误差计算得到的半正定控制权矩阵.由于提高了期望的侧倾角,线性状态空间在稳态条件下得到了解决.在稳态条件下应当为0,依据式(11)中关于求车辆侧倾动力学部分,期望侧倾角可通过如下关系式求得:
(20)
这些权重因数的初始值分别为
最小性能指标可通过求解微分方程得到
(23)
其中,P可表示为
(24)
控制器输入值uoc*可通过如下式子计算得到:
(25)
同时,针对所有状态变量导出线性反馈系数,从而调节防侧倾杆系统产生的最佳力矩值,防止车辆不稳定状态的产生.
2.2 模糊控制器的设计
由于模糊控制器具有简单实用性,开发了图3所示的模糊控制器,以研究车辆模型的侧倾阻力,该控制器主要目的为保持车辆在运动中的稳定性.

图3 模糊逻辑控制器Fig.3 Fuzzy logic controller
模糊规则主要分为4个工作步骤:模糊化、规则库的设计、近似推理和清晰化,具体阐述如下:
(1) 模糊化.这是将一个实数标量值转换为一个模糊值的过程.在这项工作中,基于状态变量和控制参数,5个状态都反映了参数的模糊控制策略的水平:极低、低、正常、高、很高.
(2) 模糊规则库.规则由一组if-then规则组成,由此形成推理机制.该规则机制阐述了状态变量与控制参数间的相互关系.
(3) 近似推理.一种由逻辑规则中的运算符构成的推理工具.一般来说,逻辑规则在状态变量之间使用AND或者OR作为连接操作符来指定足够的控制参数.
(4) 模糊化.在模糊控制规则库系统,获得最终的模糊集后,需要将其逆模糊化以得到一个数值输出量作为控制信号.最常见的反模糊化是在区域的中心,或极大域,这也是本文利用的区域.质心逆模糊法技术[11]可表述为
(26)
式中:x*为模糊化输出;μi(x)为集合隶属函数;x为输出变量.如图4所示,开发了一种模糊逻辑控制器并为整车提供设计所需的控制策略,它有2个状态变量作为输入量(侧倾角速度和横向加速度)和一个控制参数作为输出量(防侧倾力矩).设计的模糊逻辑控制器有2个输入,每个输入都对应3个中频值及9个模糊规则.因此,中频值的中心取为0.5.当车辆横向加速度和侧倾角速度增大时,根据车辆侧倾模型调整规则,控制器命令防侧倾杆系统产生更多力矩,以改善车辆操纵性能和防止侧翻.

图4 模糊逻辑控制隶属函数Fig.4 Fuzzy logic control membership function
3 仿真及分析
为了对车辆运动的稳定性进行有效评估,在正弦路面上进行运动分析,如图5所示.借助于数学软件Matlab进行数值仿真验证,仿真参数设置如下:车辆总质量m=1 070 kg,簧载质量ms=900 kg,簧载质量的高度h=0.6 m,簧上质量的距离hs=0.6 m,车辆转动惯量Izz=2 100 kg·m2,Ixx=500 kg·m2,惯性积Ixz=47.5kg·m2,前轴的距离Lf=1.1 m,后轴的距离Lr=1.3 m,前、后轮胎的转向刚度为Cf=Cr=45 312 N/rad,滚动轴刚度Kφ=65 590 N·m/rad,滚动轴阻尼系数Dφ=2 100 N·m/rad,车轮转动惯量Iw= 0.9 kg·m2,车轮有效滚动半径R=0.283 6 m,车辆行驶速度90 km/h,仿真时间为t=8 s.采用模糊逻辑控制的车辆横向加速度、侧倾角及侧倾角速度仿真结果分别如图6~图8所示.
由图6仿真曲线可知:车辆在路面行驶过程中遇到路面障碍物时,采用PID控制所产生的横向加速度峰值为11.1 m/s2,采用模糊逻辑控制所产生的横向加速度峰值为3.2 m/s2.由图7仿真曲线可知:采用PID控制所产生的侧倾角峰值为0.34 rad,采用模糊逻辑控制所产生的侧倾角峰值为0.18 rad.由图8仿真曲线可知:采用PID控制所产生的侧倾角速度峰值为1.12 rad/s,采用模糊逻辑控制所产生的侧倾角速度峰值为0.75 rad/s.综合比较,车辆采用模糊逻辑控制方法,横向角速度、侧倾角及侧倾角速度峰值较小,车辆行驶遇到路面复杂路况时抖动较小,运动相对稳定.
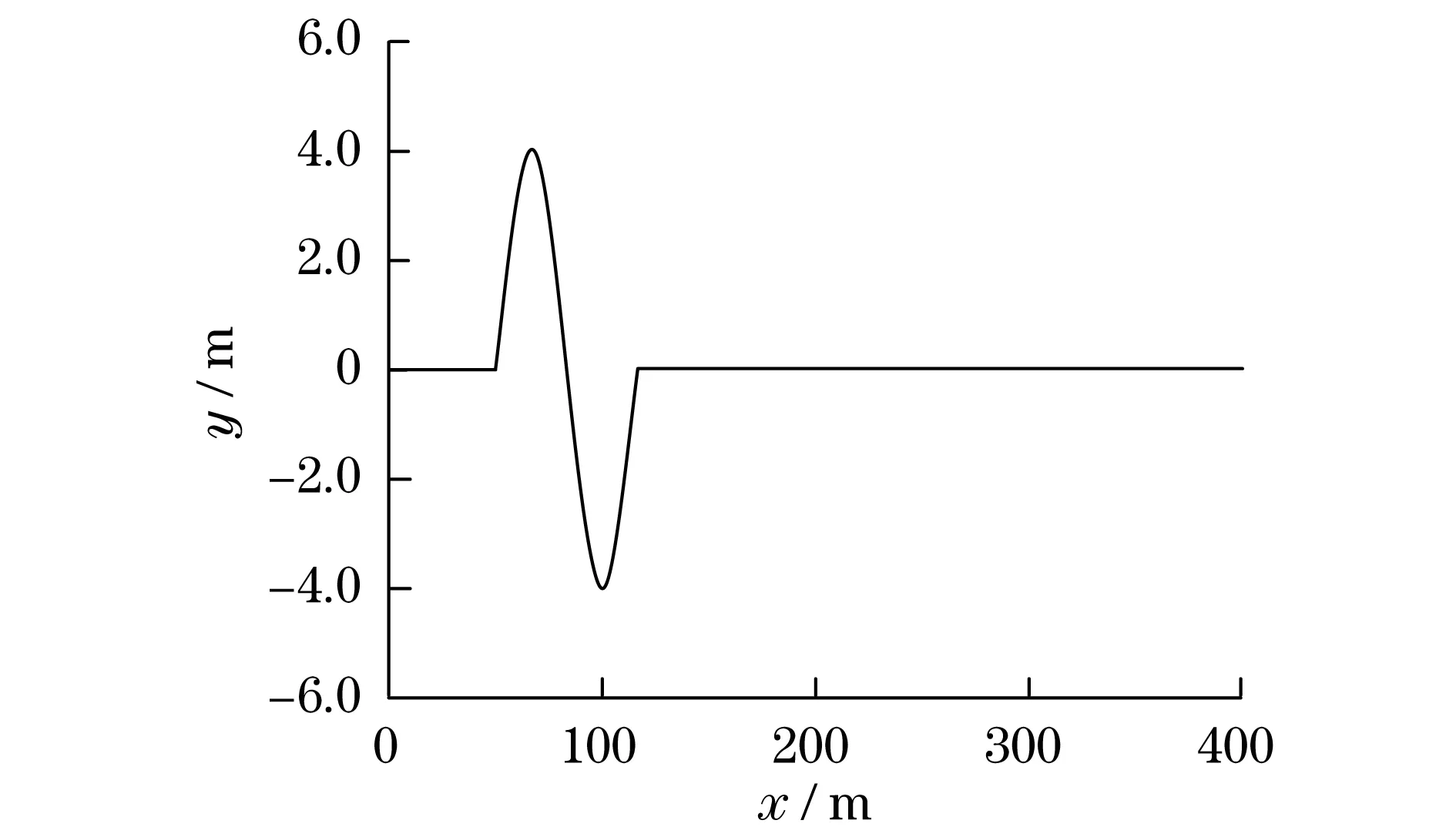
图5 正弦路面Fig.5 Sinusoidal pavement

图6 横向加速度Fig.6 Lateral acceleration
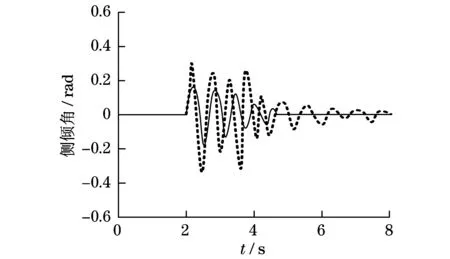
图7 侧倾角Fig.7 Side dip angle
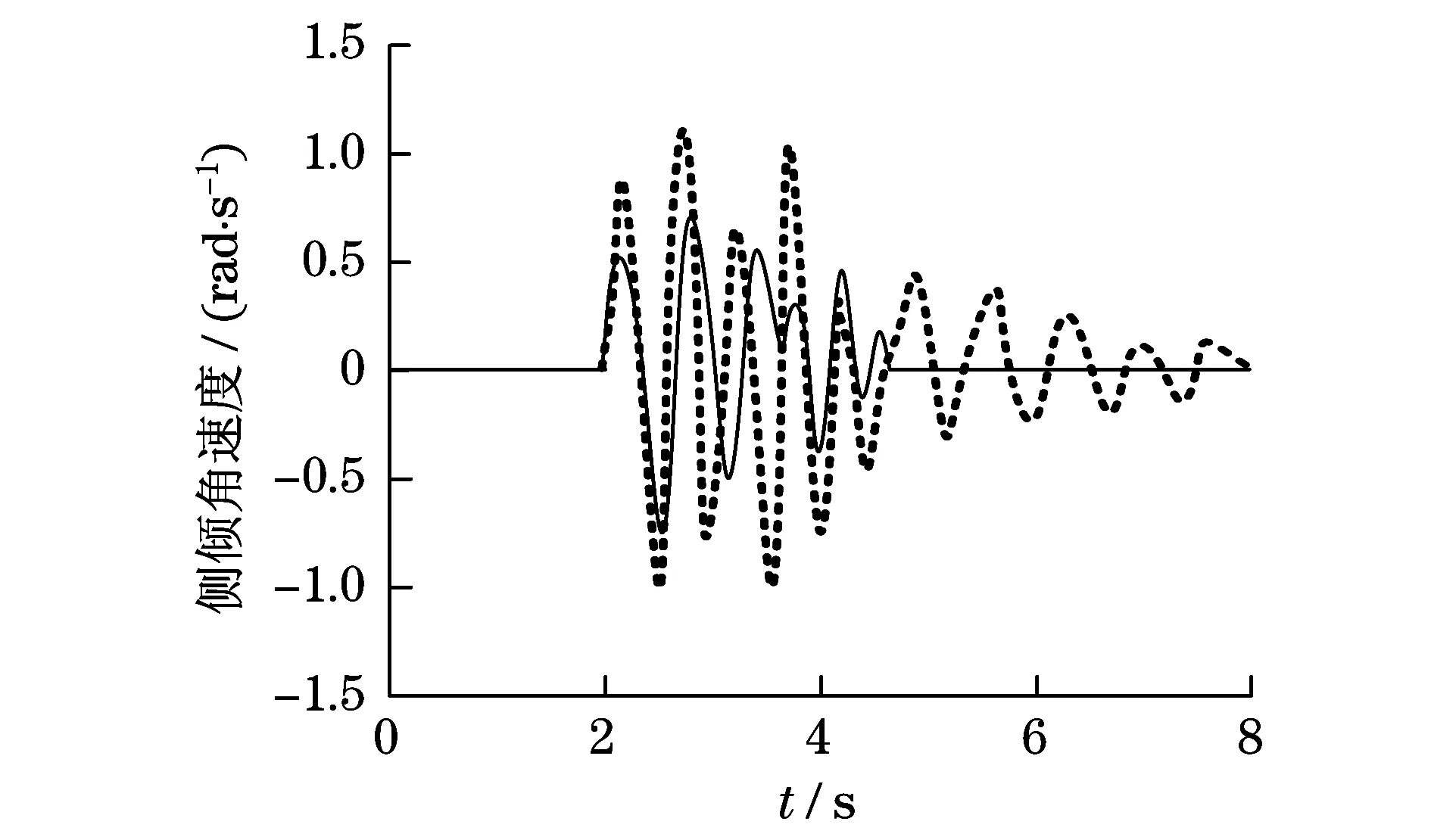
图8 侧倾角速度Fig.8 Side tilt angle velocity
4 结语
本文研究了车辆行驶稳定性模糊逻辑控制方法,建立车辆行驶侧倾模型简图,推导出车辆侧倾运动方程式,定义车辆模型几何参数,分析模糊控制法则,对车辆控制参数进行模糊化,采用模糊隶属函数设计车辆行驶的模糊逻辑控制系统.在Matlab软件中对车辆行驶产生的横向加速度、侧倾角及侧倾角速度进行仿真,并且与PID控制系统仿真结果进行了对比.仿真结果显示:在受到路面不确定路况干扰的情况下,车辆行驶采用模糊逻辑控制方法产生的横向加速度较小,抖动幅度较低,有效地避免了车辆侧翻情况的发生.

