高考数学全国卷解三角形简答题研究
潘敬贞

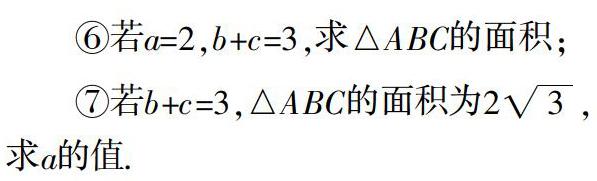
[摘 要] 解三角形是近年来全国卷考查的重点和热点内容,一般是第一道简答题. 试题难度不大,考查知识并不复杂,但每年高考学生的解答并不尽如人意,得分率不高. 全国卷解三角形简答题考查内容、考查问题比较稳定,试题命题也有一定的规律. 从考查内容、考查问题、解题思路、命题规律等角度进行研究,旨在为提高高考解三角形简答题备考的针对性与有效性,提高考生的得分率等提供参考.
[关键词] 全国卷;解三角形简答题;研究
解三角形是近年来全国卷考查的重点和热点内容,一般是第一道简答题. 试题难度不大,考查知识并不复杂,但每年高考学生的解答并不尽如人意,得分率不高. 文[1]分析了2017年高考全国课标Ⅰ卷理科第17题解三角形,由于学生忽略了隐蔽的余弦定理导致了解答并不顺利、得分率不高,并提示学生在解有关解三角形的题目时,当已知一个角或已求出了一个角一定不要忘记了余弦定理等.笔者深受启发,那学生为什么会忽略隐蔽的余弦定理呢?究其原因何在?这些问题值得我们深入研究,寻找问题之所在,对提高备考效果、促进备考效益具有重要意义.本文主要从考查内容、考查问题、解题思路、命题规律等角度进行研究,旨在为提高高考解三角形简答题备考的针对性与有效性,提高考生的得分率等提供参考.
考查内容
经过对近7年(2011-2017)全国卷试题的研究发现,解三角形简答题主要考查的内容不是很多,也不复杂,并且很稳定. 主要包括正余弦定理、三角形面积公式、和角与差角公式、诱导公式、同角公式与基本关系、三角形有关角的函数值等三角函数与解三角形的核心内容.
考查问题
经过研究近7年(2011-2017)全国卷发现,解三角形简答题主要考查的问题包括利用正余弦定理、主要三角公式(和角与差角公式、诱导公式、同角公式)、基本不等式等知识,通过转化与化归、函数与方程等思想方法,经过推理、运算,解三角形及其有关问题. 也可概括为三个方面的问题,第一是根据函数与方程思想,利用正余弦定理、三角形面积公式、所给几何图形的等量关系和已知等式,列关于三角形一个或几个元素的方程或函数解析式.第二是根据转化与化归思想,结合三角公式,将所列的方程进行变形、化简求值. 第三是利用基本不等式、三角函数对三角形的面积、周长或某一条边等进行求最值. 这三个方面的问题都是围绕着解三角形有关的元素或几何量,解决这些问题的关键是尽可能地找到已知的或隐藏的等量关系并列方程,然后结合三角公式对所列的方程进行变形、化简求解即可.
针对近7年(2011-2017)全国卷解三角形简答题考查的问题,可以将试题分成两类. 第一类试题的第一问,主要通过已知某一个等式的形式将某个角隐藏起来,要求考生将隐藏的角寻找出来,即求三角形某个角的大小或某个角的三角函数值,在求解过程中考查正弦定理、余弦定理、和角公式、诱导公式、同角基本关系、已知值求角等三角知识内容以及考查运算求解、推理等能力,突出能力立意.第二问主要考查三角形面积公式、正弦定理、余弦定理、基本不等式以及常见的数学运算(配方、开方、解方程组等),根据第一问所求出某个角的大小或某个角的三角函数值,主要从四个方面进行设问,第一是已知第一问所求出角对边的值和三角形的面积,求另外两条边的大小或求三角形的周长;第二是已知第一问所求出角对边的值,求三角形面積的最大值或三角形周长的最大值;第三是已知三角形的面积,求第一问所求出角对边的最小值;第四是已知三角形两条边的和以及三角形的面积,求第一问所求出角对边的值或已知三角形两条边的和以及第一问所求出角对边的值,求三角形的面积.第二类试题是已知三角图形以及三角图形中的边角关系、几何量的关系或值,求三角形的元素、几何量的值.
解题思路
第一类试题的第一问的主要解题思路是利用正弦定理把边化角或角化边,利用和角公式、诱导公式、降幂公式、同角基本关系、余弦定理、特殊角的三角函数值等进行求三角形某个角的值或某个角的三角函数值. 对于第一类试题的第二问通常有四种设问方法.第一种设问:已知第一问所求出角对边的值和三角形的面积,求另外两条边的大小或求三角形的周长. 解决此类问题的常用思路是利用余弦定理和三角形的面积公式分别列两个方程然后求解作答即可. 第二种设问:已知第一问所求出角对边的值,求三角形面积的最大值或三角形周长的最大值. 解决此类问题的第一种常用方法是利用正弦定理把边化角,最终将三角形的面积问题或三角形的周长问题转化为角的三角函数问题,再求三角函数的最大值,第二种常用方法是先利用余弦定理列方程,再利用重要不等式或基本不等式进行变形求解. 第三种设问:已知三角形的面积,求第一问所求出角对边的最小值.解决此类问题常用的方法是先利用三角形的面积公式列方程并化简得出两条边的乘积的值,然后利用余弦定理列方程,最后利用重要不等式进行变形求解. 第四种设问:已知三角形两条边的和以及三角形的面积,求第一问所求出角对边的值或已知三角形两条边的和以及第一问所求出角对边的值,求三角形的面积. 解决此类问题常用的方法是将已知三角形两条边进行平方,利用三角形的面积公式或余弦定理列方程并化简求解即可. 解决此类问题应注意,问题需要求几个量则需要列相应的几个方程,若根据题意所列的方程不足以解出方程中的未知数,则只能求某个元素或几何量的最值. 解决此类问题的关键是列有关元素或几何量的方程,利用三角函数、基本不等式求某个元素或几何量的值或最值.
第二类问题的主要解题思路是根据题目已知的等式和将题目中体现等量关系的条件转化为等式,从隐含的等式和条件中找等量关系,包括公式定理(正余弦定理、主要三角公式、面积公式、基本不等式)和三角图形中的线、面、角的关系. 注意,求什么(三角形的元素及其有关量)的值(范围)就列关于什么的方程(不等式),找与什么有关的等式.通过代换、运算、化简所列方程,消去与所求量无关的元素或量;求出所求量再解决相关问题.
命题规律
解三角形简答题主要考查学生对相关知识的掌握情况,考查学生函数与方程思想、转化与化归思想等数学思想方法的掌握情况,考查学生运算求解、推理等能力. 因此在命题时主要突出解三角形本质、突出能力立意等. 解三角形的本质是已知某三个元素(三角形确定),求其他元素或有关的量. 如果已知某一个或两个元素(三角形不确定),则可求出其他部分元素,并可求出某些元素或有关量的变化范围. 解三角形简答题的命题思路是间接地给出三角形的一个条件,利用另一个或两个元素的值和隐藏条件求某个元素或量的值或取值范围. 在命题过程中首先确定命题蓝图,如:给出三角形中的一个条件. (1)已知一个元素,求另一个元素;(2)已知另一元素,求某个元素或有关量的取值范围.再确定命题模坯,如:在△ABC中,AB=2AC. 若C=90°,求B;若AB=2,求△ABC面积的最大值.
示例:第一类试题第一问,首先确定某个角的大小或某个角的三角函数值,又由于如果已知某个角的正弦值,但在区间(0,π)内角不唯一,因此一般选择余弦或正切进行设计,再考虑考查内容,从正弦定理、余弦定理、和角公式、诱导公式、配角、同角基本关系中选择几个进行考查.
题目:在△ABC中,内角A,B,C的对边分别为a,b,c.
只有当教师全面了解解三角形考查内容、考查问题、主要解题思路和掌握命题规律,明确能力立意和学科核心素养,选编针对性强的试题指导学生练习,使学生熟练掌握解三角形相关知识,掌握函数与方程思想、转化与化归思想等数学思想方法和主要解题思路,提高学生运算求解、推理等能力,提高高考备考的针对性与有效性,提高学生得分率方可真正落到实处.
参考文献:
[1] 温和群. 隐蔽的余弦定理——2017年高考试题有感[J]. 中国数学教育(高中),2017(10):58-60.

