“图形的旋转”学生学习障碍分析——基于学生学习过程的研究

◇朱育红

根据以往的教学经验，有关图形旋转的教学内容，看起来简单，学起来并不容易。即使学生能熟练说出图形旋转过程中的关键要素——旋转中心、旋转方向和旋转角度，但遇到具体问题时，往往有“剪不断理还乱”的感觉。在教学时，虽然主张让学生多操作，帮助学生建立并积累数学经验，但学生还是感觉有困难，教师普遍认为反复训练加个别辅导定能解决问题。然而，“图形的旋转”的内容真的无法让学生真正理解并掌握吗？真的无法用比较清晰的数学语言来描述旋转运动的过程吗？学生的思维路径是怎样的？学生的困难或障碍是什么？

基于这些问题，我们以北师大版教材六年级下册第三单元 “图形的运动”中 “图形的旋转（二）”一课的“情境和问题串”为媒介，通过课前访谈、课堂观察和后测，了解学生在学习过程中的表现，特别观察：在学习过程中，学生到底是怎样解决问题的？他们有哪些思考方法？这些方法可以分成几种类型？哪些方法与教材一致？哪些方法与教材不一样？学生的方法是否体现了不同水平？教师应该提供什么样的学习支持？在这种支持下，学生对知识的理解程度如何？

为此，我们选择样本学生37人进行调研。下面从学习过程、学习效果两个方面介绍实证研究的情况。

一、学生的学习过程

1.关于“画出图中的小旗绕点M顺时针旋转90°后的图形”的学习过程（如图1）。

图1

有33人能够先画出旗杆，借助旗杆的旋转画出旗面；有4人需提示方能完成。可以看出大多数学生能借助一定的生活经验完成题目，而且旋转图中有旗杆，有利于学生借助线段旋转的经验解决整个图形的旋转问题。对学习有困难的学生（以下简称学困生）来说，存在两个障碍点：一是不能主动发现并利用线的旋转来思考、解决问题；二是如何确定旋转前后对应边或点的位置。

在访谈过程中，发现有一名学生无从下手解决这个问题，教师启发他“可以先找到旗杆旋转后的位置”后，他画出了旗杆旋转后的正确位置。看来教材引导学生进一步思考的“提示语”，对学困生有很好的提示作用。

在解决问题1后，教师追问学生：画整个图形时要注意什么？学生均能从旋转中心、旋转方向和旋转角度等方面进行交流。

但没有学生提出在画旗面时应注意什么，而这个问题正是学生要面对的关键问题——运用旋转的三要素可以解决一条线段的旋转问题，但是其他边或点在旋转的过程中发生了怎样的变化呢？这正反映出学生不能将图形旋转的表征与图形特征的判断相融合、相统一。这说明只记住旋转的三要素不足以解决平面图形的旋转问题，还需重视图形旋转活动中的经验积累。

2.关于“画出三角形ABC绕点A顺时针旋转90°或绕点B逆时针旋转90°后的图形”的学习过程（如图2）。

图2

在“画小旗旋转90°后的图形”活动的基础上，成绩中等及以上学生均能画出三角形ABC绕点A顺时针旋转和绕点B逆时针旋转90°后的图形，而且能够从含有中心点的线段（直角三角形的直角边）入手解决问题。对学困生来说，存在的障碍点是关注线的旋转的同时忽略了绕哪个点旋转，并且依然存在不能确定旋转前后对应边的位置的问题。画平面图形的旋转，对空间观念的要求比较高，教师需要帮助学生弄清楚“正确画图的关键”——厘清旋转中心、旋转方向和旋转角度，帮助学生学会借助操作、想象等活动确定旋转前后对应线段的位置。所以教材中介绍了方法“想一想，也可以剪一个同样大的三角形摆一摆”，对学困生解决问题有一定的帮助。

（1）图2左图中问题的解决与分析。

图2左图中解决的是画出三角形ABC绕点A顺时针旋转90°后的图形，有约83.8%的学生能够正确画出三角形旋转后的位置；有约16.2%的学生不能独立完成，需要经过提示或模拟操作的过程方能完成。

有趣的是，约91.9%的学生在解决这个问题时，从线段AC入手解决问题，只有约8.1%的学生从线段AB入手解决问题，没有学生从线段BC入手思考。学生交流想法时说，从三角形的直角边入手思考方便，因为直角边正好和方格纸中的线重合，很容易确定旋转的角度；线段AB旋转后与AC重合了，不好画。经过交流，学生达成共识，先画线段AC或AB都可以，这是三角形的两条直角边。

出现的主要错误类型如图3～图5所示。

图3

图4

图5

类型Ⅰ：对旋转中心不清楚，有2人。如图3，错将点C作为旋转中心，反映出此类学生没有掌握线的旋转方法。以点A为旋转中心，他们能想到从与点A有关的线段AC入手思考，这是很好的，但随之在头脑中不能建立点A固定不动，而点C带动线段AC实现顺时针旋转90°后的样子，这类学生不能在头脑中形成清晰的表象。

类型Ⅱ：不能确定旋转后对应边的位置，有4人。如图4和图5，此类学生能够从线段AC入手，正确找到线段AC绕点A顺时针旋转90°后的位置，而判断旋转后线段AB的位置时出现错误。实际上从线段的旋转表征到二维平面图形的旋转表征，解决问题的过程不单纯是表象运动过程，而是较复杂的思维过程，需要将平面图形的旋转与图形的特征相结合进行判断。当图形旋转的表征和基于几何概念的判断不清晰时，就会导致问题不能顺利解决。此时需要将动作感知、表象和概念相互联系。

（2）图2右图中问题的解决与分析。

图2右图中是画出三角形ABC绕点B逆时针旋转90°后的图形，其中约67.6%的学生能够独立、正确完成，约32.4%的学生不能独立完成，需要经过提示或模拟操作的过程方能完成。

出现的主要错误类型如图6～图9所示。

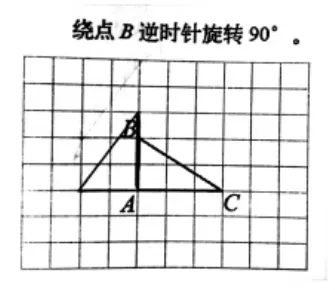
图6

图7

图8

图9

类型Ⅰ：对旋转中心不清楚，有2人（如图6）；把旋转方向弄错，有5人（如图7和图8）。

类型Ⅱ：旋转策略不清，有5人。如图9，此类学生能够从线段BA入手，正确地将线段BA绕点B逆时针旋转90°，而判断旋转后线段AC的位置时出现错误。

我们可以看到，画出三角形ABC绕点B逆时针旋转90°比绕点A顺时针旋转90°后的图形的错误率高，可能的原因是：

其一，部分学生认为解决逆时针旋转时容易出现错误。教师追问此类学生，他们说：想着逆时针，不知道怎么就比画成顺时针了。但不少学生有减少此类错误的好方法，如图10，把图形旋转的基本要素在图上清晰地表示出来，展现自己的思维过程。

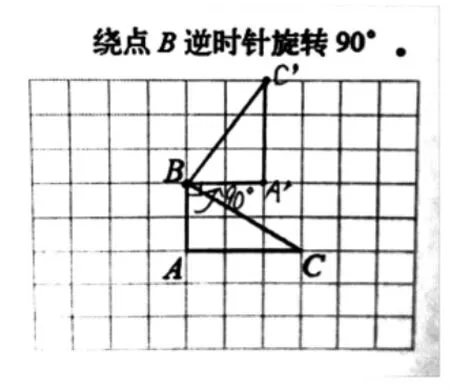
图10

其二，由于与旋转中心点相连接的两条线段，一条是直角三角形的直角边，另一条是斜边，而在方格纸上不能直接确定斜边旋转后的位置，与刚刚积累起的解决图2中左图的经验有所不同。这就需要学生根据三角形的特征，确定先解决哪条线段的旋转比较简单，思维的过程更复杂了。

3.关于“与同伴说说你是怎么画的，需要注意什么”的学习过程。

多数学生能够结合画的过程总结方法，并能提出需要注意的地方；只有1人忽略了旋转中心。其中学生表达方式略有不同，如图11，有的学生概括性强，有的学生描述具体，而学困生考虑问题不全面。

图11

二、学生的学习效果

经过教材上问题串的学习，有多少学生能够达到基本要求？达不到要求的学生，其主要困难是什么？该如何提供学习支持，帮助其理解知识呢？下面通过教材中的练习和延迟后测的分析进行说明。

学生完成正文中的三个问题后，逐一完成教材“练一练”中的三道题（题略）。完成情况如表1。

表1

从上面数据来看，学生基本体会到图形旋转的基本要素，并能在方格纸上画出一些简单图形绕图形上某一点旋转90°后的图形。在平面图形的旋转中,使用语言的准确性提高,头脑中二维平面图形的旋转表征清晰。学生在解决平面图形的旋转时,采用的是旋转加特征判断的策略,或者是旋转为主,辅之以特征判断,或者是特征判断为主,辅之以图形的旋转。其发展趋势是:平面图形的旋转表征清晰、准确、灵活、多样,特征判断从单维发展到双维,从不稳定到较稳定。

一周后进行了延迟后测，后测结果表明，学困生依然存在障碍，主要是由于这部分学生空间旋转表征与基于几何概念的判断还不清晰时需要依据动作感知。当几何概念较明确时,在一定程度上会加强空间旋转表征的清晰性,从而就可摆脱对动作的依赖。