“画”出来的精彩——例谈“画图中深度理解数学”的实践研究

◇董文彬

画图是学生数学学习中最为丰富的路径。如何帮助学生亲近数学、走进数学？如何帮助学生深度理解数学？如何变冰冷的数学学习为火热的有温度的数学思考？近几年，我带领学生一起进行了“画图中深度理解数学”的实践探索，与大家分享。

一、画图中直观表征数的意义

在“数的认识”领域，学生的认识对象主要是整数、小数和分数。从计量走向计数，数的相关概念是抽象的，在理解数的意义教学中，我们需要帮助学生寻求适合于他们的表征与理解方式。在北师大版教材四年级下册“小数的意义”教学中，我们进行了这样的尝试：画图表示你对3.33的理解。

图1是学生画出的“人民币实物模型图”，三年级时学生曾借助人民币初步认识了小数，这为学生四年级时再认识小数积累了学习活动经验，学生能够将这些经验迁移到小数的再认识中，通过画出形象的人民币单位模型图将抽象的计数单位进行直观化理解。

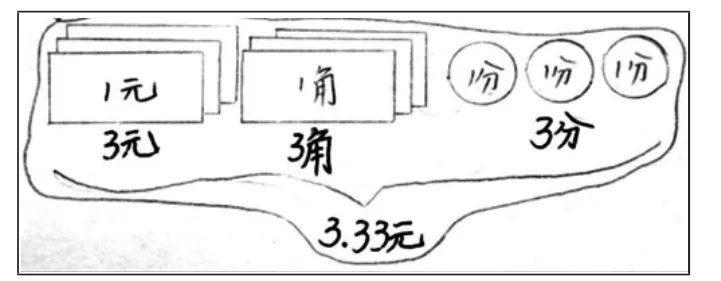
图1

图2 是学生画出的“长度数线模型图”，从低年级认识“10以内的数”开始，数线就是学生认识数时的重要模型，同时基于对“米、分米、厘米”这些长度单位的认识，学生将两部分学习经验合而为一拓展到表征数的意义中，从而他们不难表达对3.33的理解。

图2

图3 是学生画出的“计数器图”，图4是学生画出的“数位顺序表”，学生借助计数器和数位顺序表这两个重要的工具，将所要表示的数写在各自相应的数位上，简明地将抽象的计数单位，以及数中含有的计数单位的个数表示出来，明确3.33中每个“3”所表示的不同意义，从位值、数的组成的角度直观理解3.33这个小数。

图3

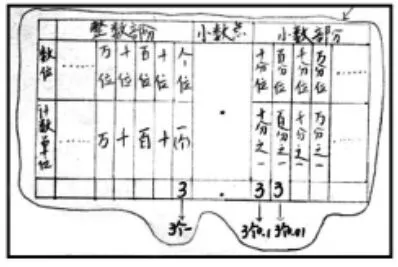
图4

图5 是学生画出的“方格面积模型图”，可以说，方格图是学生认识数的过程中又一个十分重要的直观模型。学生借助方格图直观地理解计数单位，将抽象的数形象地表示出来，清晰地建立“计数单位”的概念，深刻地理解“数就是计数单位个数的累加”的核心实质。

图5

从学生画出的这些简明、形象的作品中，我们能够看到学生学习活动中所积累的实践经验和思维经验，这些经验为学生建立计数单位的表象，直观地表征、理解数的意义起到了“助力”的作用。

二、画图中深化理解数的本质

在数的认识学习中，随着问题变得复杂和认知冲突的发生，学生对数的意义的理解是分层次的，对数的本质的认识逐步深化。能否继续引导学生通过画来进一步深化对数的再认识呢？同样在“小数的意义”教学2课时后，借助教材中的习题资源，我进行了这样的尝试：0.3时是多少分呢？画图表达你的想法。

在这个问题中，“时”与“分”的六十进制关系会对学生造成认知上的冲突和障碍。基于对小数意义的理解，学生画图探索解决问题的思维路径（如图6），在理解小数与十进分数之间内在联系的基础上，进一步深化了对小数意义的再认识及对小数核心本质的深度理解。

图6

三、画图中理解数的运算

如何帮助学生通过画图来直观理解抽象的数学运算？我在北师大版教材三年级上册“混合运算”中做了以下尝试：面包每个3元，蛋糕每个6元。胖胖买1个蛋糕和4个面包，应付多少元？先画图表达你的思考，再根据图的意思试着列出算式解答。

借助画直观图（如图7、图8），学生或呈现解决问题的思维路径，或直接表示思考的过程与结果，或形象刻画其中的数量关系，或基于对运算意义的理解表示运算的过程与结果。具象的图形语言背后承载的是学生或隐或显的对混合运算算式的抽象过程，更是对混合运算的意义、运算顺序的合理性的独特理解。这正是以适合学生自己的方式深度理解数学的过程。

图7

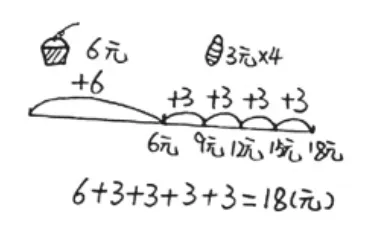
图8

四、画图中感悟数学内在的联系

数学的知识、思想、方法之间存在着隐藏的、抽象的联系。但在学情调研中，我们发现学生因感悟不到这种内在的联系，经常发生 “错误”的数学思考现象。

图9是四年级学生在小数混合运算能力测试中常出现的一种经典错误。不难看出，在进行数学运算时，学生没有感悟到不同运算表征之间的联系与区别，不能正确地进行数学运算，还理所当然地认为这样运算很“合理”。

图9

为此，我在“小数混合运算”的教学中展开了实践研究。

淘气这样计算对吗？为什么？画图解释背后的道理。

以上两道题的运算过程和结果，都与原题之间存在着一定的内在联系，这样计算的道理是什么？如果错了，问题出在哪里？如果学生能够通过画图将运算过程不同表征之间的联系直观地呈现出来，学生就能真正理解“这样计算”背后的道理。

“面积模型”图是学生的已有经验（如图10、图11），通过画图学生能够体会到：一是图形的长、宽及面积与小数运算之间存在的联系，二是运算过程不同表征之间存在的联系。在小数运算的学习中，让学生经历画直观图研究运算的过程，不仅可以帮助学生理解算理，还能够沟通、感悟到图形表征与运算表征之间、不同运算表征之间的联系。层层剥茧，感悟联系，只有看到“错误背后的真相”，学生才能真正理解运算的本质。如此辨析、化错，岂不妙哉？

图10

图11

五、画图中探究解决问题的策略

在解决稍复杂的数学问题时，学生一般会采用什么样的策略方法？我进行了这样的测试研究。测试对象是使用北师大版教材的三年级学生，他们刚刚初步认识了分数，但还没有学习五年级的“分数意义”，更没有接触分数乘除法的运算。测试内容是让学生尝试解决问题：“一盘草莓，小明吃了12个，占这盘草莓的。这盘草莓一共有多少个？”由于解决此问题要用到没有学过的内容（按照教材编排五年级才学到），因此有一部分学生不会解决。但从能够解决问题的学生的作答中，我惊奇地发现：学生大多是通过画直观图的方式来探究解决问题的策略。

一是学生能根据学习经验，画出线段图来描述数学问题（如图12），借助线段图来刻画、表征对这个分数意义的理解，从而理解题目含义，分析数量关系，寻求解决问题的思路：将分数问题转化为整数运算问题，“先求每一份，再求几份”，将其转化为学过的“归一问题”进行解决。

图12

二是学生用画出的长方形、圆饼图等面积模型来刻画数学问题（如图13），把画直观图，特别是长方形图直接作为解决问题的工具或手段，用画图的方法直接表示解决问题的思考过程与结果。学生用适合于自己理解的画图的方式表达对问题的理解。

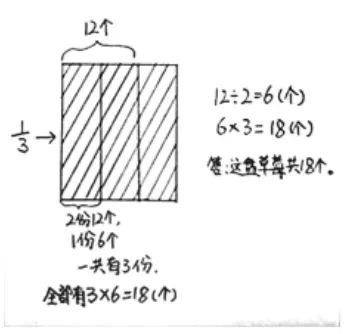
图13

三是基于对分数意义的理解（如图14），由部分想象整体，学生通过画圆圈图、点子图的方法表示已知数与未知数之间的数量关系，根据几何直观寻找解决问题的思维路径，再分步列式，通过计算解决问题。

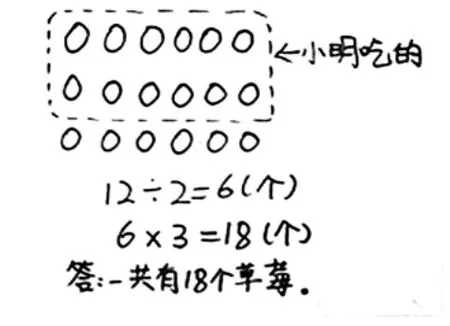
图14

由此可以看出，学生平均分的对象已经由“个”扩展到“群”，从单一整体的长度模型、面积模型扩展到多个物体或图形作为整体的集合模型，借助画图学生对分数意义有了进一步的理解。

运用画图的方式，学生可以直观、简明地描述题意，反映数量关系，表示理解和解决问题的过程，积累解决问题的思维经验，逐步体会“抽象”的数学思想，探索解决实际问题的策略。