驻波法与相位比较法声速测量实验的对比研究*

石明吉 罗鹏晖 刘 斌 于家辉

(南阳理工学院电子与电气工程学院 河南 南阳 473004)

1 引言

声波是一种在弹性媒质中传播的纵波，随着超声学研究的迅速发展，声学检测在实际应用中已越来越广泛，对超声波传播速度的测量在超声波测距、无损检测、定位、测量气体温度瞬间变化等方面具有重大意义[1]．超声波具有波长短、可定向的优点，因此，常被用作测量声速[2]．目前，大学物理实验中的声速测量方法主要有两种：驻波法(也叫共振干涉法)和相位比较法[3]．驻波法是让声波发射器发出超声波，超声波遇到接收器被反射，反射波与入射波叠加，形成驻波．移动声波接收器，将接收器产生的电信号送给示波器进行观察．当接收器依次经过波腹、波节、波腹、波节等的时候，示波器上波形的幅值(幅值与声压成正比)依次出现最小、最大、最小、最大……由于相邻两个波腹或波节之间的距离等于半个波长，进而得到波长，然后将波长与频率相乘就得到波速．相位比较法是将信号源的信号利用分支器一分为二，一路直接给示波器的一个通道，另一路给声波发射器，将声波接收器产生的信号接示波器的另一个通道，然后将示波器调整到X-Y工作状态，得到利萨如图形．改变接收器位置，则接收器产生的信号的位相开始变化．假设在某一位置，两路信号的相位差是2π的整数倍，则利萨如图形是一三象限的一条直线．由于沿着波传播的方向，每走一个波长，位相改变2π，一三象限的直线就重复出现一次．将出现一三象限直线的接收器位置记录下来，相邻两个位置的间隔就是波长，有了波长，再乘以频率就得到波速．不管是驻波法还是相位比较法，都是用眼睛观察示波器进行测量．测量的时候，为防止回程差的影响，不能回头，只能朝一个方向不断地移动测量，不容易测准确；利用人眼观察、读数、移动，费时费力．为解决这个问题，有必要研究全自动声速测量系统．

2 整体设计

自动声速测量系统要完成两个任务：一个是通过单片机控制步进电机驱动器，由驱动器驱动步进电机转动，通过丝杠实现声波接收器的运动；另一个是采集卡采集数据，传给上位机，在上位机界面上画图并保存数据．

2.1 驻波法

为了实现声压测量的自动化，有必要将接收器产生信号的峰值或有效值进行数字化，AD637有效值检测模块可以实现这一功能．将接收器产生的信号送到AD637模块，AD637输出的直流电压信号送给采集卡采集．系统的框图如图1所示．

图1 全自动驻波法声速测量系统框图

2.2 相位比较法

为了相位差测量的自动化，有必要将相位差测量数字化，AD8302相位差测量模块可以完成这个任务．将来自信号源的信号和声波接收器产生的信号输给AD8302相位差测量模块，AD8302输出与两信号相位差成反比的直流电压信号[4]，将这一信号送给采集卡采集．系统的框图如图2所示．

图2 全自动相位比较法声速测量系统框图

3 实验结果与分析

用驻波法测量，室温17.8 ℃，信号源vPP=11 V，开始调到共振频率40.08 kHz，开始时，声波发射器与声波接收器之间紧靠，由近及远测量，设置测量点数目为6 000个，时间间隔300 ms．将得到的数据利用Oringin7.5 进行处理，结果如图3所示．

图3 驻波法声速测量实验中声压与位置的关系

根据驻波理论，相邻的波腹与波腹之间、波节与波节之间的距离都是半个波长．所以，既可以根据声压振幅的各极大值点位置计算波长，也可以根据声压振幅的各极小值点位置计算波长．根据声压振幅的各极大值点位置，可以计算出

λ=8.75 mm

所以

v=λf=350.7 m/s

根据声压振幅的各极小值点位置，可以计算出

λ=9.05 mm

这样可以算出

v=λf=362.7 m/s

(1)

其中

v0=331.45 m/s

T0=273.15 K

T=(t+273.15) K=290.95 K

代入式(1)后算出17.8 ℃时声速的理论值

v′=342.1 m/s

对比可知，驻波法测量时，通过极大值点计算波速比较准确．这与文献[5]和文献[6]的观点相吻合．由于次峰的出现，如3 642，4 105和 4 579这些位置的前方，使得极小值点的位置不准，无法准确计算波长．次峰不仅影响极小值点的位置，也会对极大值点的位置产生影响．比如，在极小值5 321的后面，应该出现一个极大值、单峰的地方却出现具有两个极大值的双峰，两个极大值的差别很小，无法区别哪个是真正的极大值．这一现象与文献[7]和文献[8]所提的问题是一脉相承的．声波多次反射叠加，考虑到损耗，在用驻波法测量波长时，不仅要测量极大值的位置，还要比较极大值的振幅以排除次峰的干扰．

用相位比较法测量，室温17.8 ℃，信号源vPP=11 V，频率调到共振频率40.08 kHz，开始时，声波发射器与声波接收器之间紧靠，由近及远测量，设置测量点数目为6 000个，时间间隔300 ms，结果如图4所示．

图4 相位比较法声速测量实验中相位差

根据极大值计算，λ=8.76 mm，因为f=40.08 kHz，所以，v=λf=351.1 m/s．

根据极小值计算，λ=8.81 mm，因为f=40.08 kHz，所以，v=λf=353.1 m/s．对比可知，相位比较法测声速时，采用极大值计算是比较准确的，结果与驻波法测声速利用极大值点计算的结果几乎完全相同，差别仅有千分之一．用极小值计算的结果，差别略大．为寻找原因，将驻波法和相位比较法的测量结果绘制到同一幅图中，如图5所示．

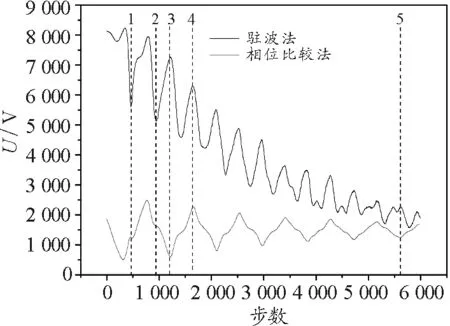
图5 驻波法和相位比较法的测量结果的比较

对比两条曲线发现：相位比较法曲线上的极值点(包括极大值点和极小值点，虚线3和4所示)与驻波法曲线上的极大值点近似地一一对应；驻波法曲线上的极小值点与相位比较法曲线上峰两侧的山腰位置近似地一一对应(虚线1和2所示)；驻波法测声速，信号随发射器和接收器之间距离的增加而迅速衰减，相位比较法测声速，信号随着发射器和接收器之间距离的衰减比较缓慢；驻波法曲线受次峰的影响比较明显，而相位比较法基本不受次峰的影响．所以，相位比较法测声速整体要比驻波法测声速要准确．

此外，当发射器与接收器距离较大时，可以利用相位比较法曲线帮助确定驻波法曲线的真正极大值位置．比如，在极小值5 321的后面的双峰(虚线5所示)，仅凭驻波法是很难确定哪个是真正的极大值点．但是，如果参考相位比较法曲线，就可以很容易地确定右边那个峰值点是真正的极大值点．当然，也可以利用驻波法曲线来帮助理解相位比较法曲线，比如，相位比较法曲线在450左右有一个小肩峰，如虚线1所示，这里本不该出现这个肩峰的．从驻波法曲线上看到在462处有一个极小值，其右侧峰位是789的这个峰形状与其后1 217，1 638处的峰很不相同，其左侧明显是受到次峰的影响，所以，对应在相位比较法曲线上的该肩峰不能认定为极大值点．在相位比较法曲线上出现这个肩峰应该对应一种实验现象．重新回到传统的相位比较法声速测量实验中，当发射器和接收器之间的距离较小，利用示波器合成利萨如图形观察时，在两次一三象限直线的位置之间有时会观察到一个比较小的一三象限直线位置．就是这个现象与相位比较法曲线上的这个肩峰对应．所以，如果是用传统的相位比较法测量声速，这个位置就不能算．

4 结语

搭建了全自动声速测量系统，利用有效值检测模块将声压数字化，实现了全自动驻波法声速测量．利用相位差测量模块将相位差数字化，实现了全自动相位比较法声速测量．将驻波法和相位比较法的数据进行比较，可以更好地发现并减小次峰的影响，提高声速的测量精度，增加理解声速测量问题的角度．