悬而未决，“转”出精彩——“旋转法”在解决与线段数量有关问题中的运用

☉江苏省苏州工业园区星海实验中学 戴 惠

一、知识背景

旋转变换作为几何的三大变换之一，常常蕴含了全等、相似、勾股定理等很多知识点，对学生分析问题和解决问题的能力有较高要求，往往具有较大的难度和区分度.九年级学生经过一轮复习后，对于此类指明“旋转”的题目基本会解决.但是对没有出现“旋转”字眼的题，学生对此常感到束手无策.此时我们可以试将图形的某一部分作适当旋转，突破思维瓶颈，找到解题思路.

二、教学目标

1.知识与技能

当已知条件比较分散时，考虑“旋转法”，把分散的条件通过旋转的方式重新整合，构造特殊图形，进而解决问题.

2.过程与方法

在数学解题中，有时用“动”的观点来处理“静”的问题，即“化静为动”，让学生深刻的体会“从变化中找不变”的基本解题思路.

3.情感、态度与价值观

从旋转的角度思考问题，提高空间想象能力和逻辑思维能力.

三、教学过程简录

片断（一） “旋转法”的引出与认识

例1 如图1，在正方形ABCD中，E，F是BC，CD边上的点，且∠EAF＝45°，连接EF.

求证：EF＝BE＋FD.

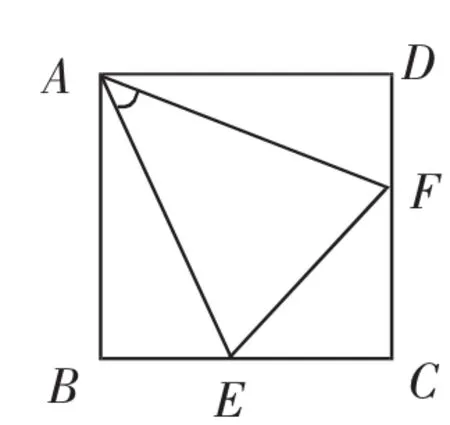
图1

设计意图：此题以我们熟悉的正方形作为载体，线段EF、BE、FD位置分散，常用方法为“截长补短”法.启发引导学生从旋转的角度去思考问题，初步认识 “旋转法”.

师：分析题目条件，你想到了什么？

生（齐）：“截长补短”法.

师：实物投影展示正确的解法.

师（启发）：几何画板演示△ABE旋转至△ADE′过程，从旋转的角度考虑，以点A为旋转中心，将△ABE逆时针旋转90°，如图2请问△AEF≌△AE′F依然成立吗？

生：成立，∠BAE=∠DAE′，∠BAE+∠FAD=45°，可以得到∠DAE′+∠FAD=45°，即∠E′AF=45°，通过SAS证明全等.

图2

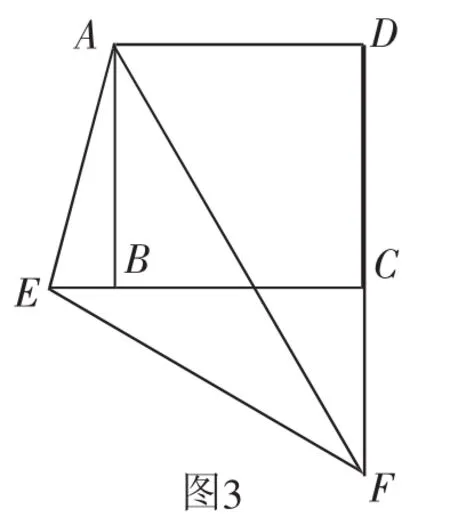
图3

图4

片断（二） “旋转法”的探索与归纳

变式1 如图3，在正方形ABCD中，∠EAF=45°，它的两边分别交CB，DC的延长线于点E、F，线段BE，DF和EF之间又有怎样的数量关系？

设计意图：此题为例1的变式，∠EAF从在正方形的内部变成有部分在正方形内部，同样使用“旋转法”可以解决问题.让学生感知“旋转法”的思路，体会用运动的观点思考问题，“化静为动”，让学生深刻地体会“从变化中找不变”的基本解题思路.

师：这道题跟例1的区别在哪里？我们先猜测一下三条线段之间有什么数量关系？

生（齐）：DF=BE+EF.

师：怎么证明呢？我们能不能也使用旋转的方法解决它呢？

生（齐）：将△ABE旋转至△ADE′，如图4.

师（追问）：旋转的目的是什么呢？

生1：使得DE′=BE，DF-BE=E′F，只要证EF=E′F即可.师（追问）：怎么证线段相等？我们常用方法是什么？生（齐）：全等，对应边相等.

师：证哪两个三角形全等呢？

生2：通过SAS证明△AEF≌△AE′F.

师：几何画板演示△ABE旋转至△ADE′过程，我们将这样的方法称为“旋转法”.什么情况下我们可以使用“旋转法”呢？

生：已知条件中线段的位置不交分散，有公共顶点，有相等的边……

师：共点——旋转中心；相等的线段——对应线段；旋转角度——旋转角.（板书）

通过构造全等三角形，转移线段，寻找线段间的数量关系.

变式2 如图5，在四边形ABCD中，AB=AD，∠B+∠D=180°，且∠EAF=∠BAD.

（1）点E、F分别在边BC、CD上，试说明EF=BE+DF；

（2）如图6，点E、F分别在直线CB、DC延长线上，线段BE、DF和EF之间又有怎样的数量关系？

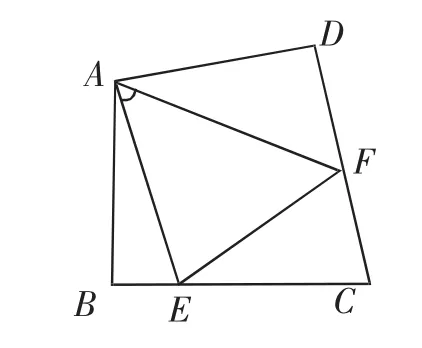
图5

图6

设计意图：此题作为学生自主练习题，是上面两道的变式，正方形、45°角的特殊关系一般化，“半角模型”.一方面检验学生是否学会使用“旋转法”，另一方面让学生体会“从特殊到一般”的数学思想.这两道题请两位同学到讲台前讲解，激发学生学习兴趣.在解决问题的过程中，培养学生举一反三的数学能力.

片断（三） “旋转法”的运用与巩固

例2 如图7，在等边三角形△ABC内有一点P，PA=2，PB=，PC=1，求∠BPC的度数.

设计意图：此题具备了数学的简洁之美，条件之间没有直接联系，不再问边的关系，而是换成了角度，学生对此束手无策.但当我们从旋转的角度去思考该问题时，转移相关线段，就会豁然开朗，柳暗花明.

图7

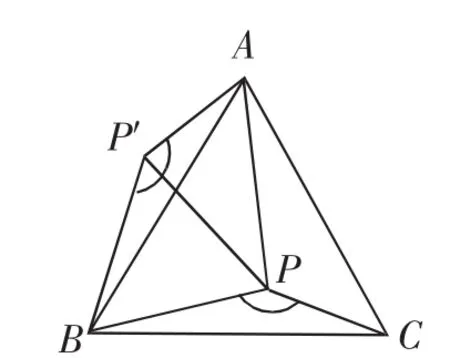
图8

生（齐）：勾股定理

师：这里有直角三角形吗？

生（齐）：没有.

师（启发）：那这里是不是也可以旋转呢？通过旋转某个三角形，转移某些线段，进而构造直角三角形呢？大家试一试.

生1：将△PBC进行旋转，如图8.

师：如图8，几何画板演示旋转过程.我们想要的直角三角形出现了吗？

生（齐）：没有，再连接PP′.

师：很好，将我们要求的∠BPC转化成两个角的和，此时∠P′BP=60°且BP=BP′，我们得到△P′PB是等边三角形，得到∠BP′P=60°.另外一个角∠AP′P又是多少度呢，你会吗？

生2：90°，根据勾股定理的逆定理得到.

师：非常好，一起告诉我∠BPC的度数.

生（齐）：150°

师：你感受到了旋转法的奇妙之处了吗？

图9

变式1 如图9，在正方形ABCD内有一点P，∠BPC=135°，BP=，PC=1，求AP的边长.

设计意图：此题作为学生练习题，载体等边三角形换成正方形，已知条件既有边的关系，又有角的关系，在解决问题的过程中，培养学生融会贯通的能力.

片断（四） “旋转法”的拓展与提升

例3 （2015·常州）如图10，在⊙O的内接四边形ABCD中，AB=3，AD=5，∠BAD=60°，点C为弧BD的中点，则AC的长是__________.

设计意图：展示中考题，激发学生攻克难题的决心.学生通过积极思考和探索，把握命题规律，提炼问题本质.一题多解，通过比较让学生切实体会旋转法的奇妙作用，调动学习积极性.

师：哪位同学来挑战一下这道中考题？

生1：C为弧BD的中点可以得到CB=CD，将△ACD进行旋转，如图11.

图10

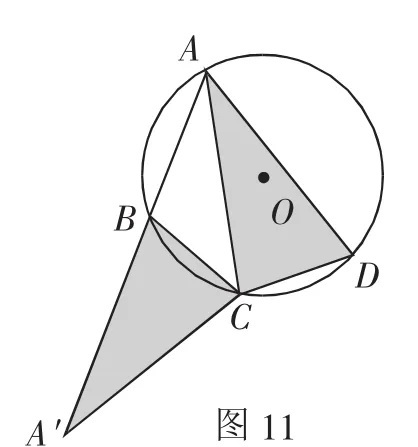
图11

师（追问）：这里四边形ABCD有什么特殊性使得我们可以选择使用“旋转法”.

生1：⊙O的内接四边形对角互补，符合我们的“旋转法”.

师（追问）：然后我们如何做呢？

生1：在△AA′C中作AA′边上的高.

师：接下来我们利用三角函数、等腰三角形性质等就可以解决.

设计意图：问题再次升级，将学生刚刚已经熟悉边角关系以直线解析式的形式呈现，给人耳目一新的感觉.难度提升一个台阶，对学生的能力要求进一步提高.通过 “转化的思想”，通过直线解析式可以得到边角关系，同样使用“旋转法”可以解决问题.

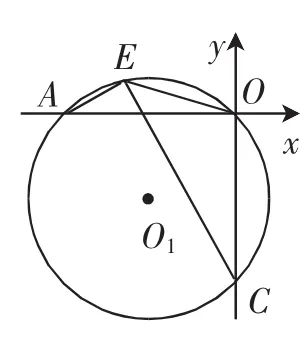
图12

图13

师：在圆中，圆周角90°，我们常作什么辅助线？

生（众）：连接AC，AC为直径.

师：EC-EA如何处理呢？“旋转法”好用吗？

生2：以O为旋转中心，将△OAE逆时针旋转90°，如图13.

师：EC-EA=EE′，△OEE′为等腰直角三角形，则EE′∶EO为.能否将△OAE，以A为旋转中心顺时针旋转90°呢？课后思考.

四、教后反思

对于“空间与图形”的教学，《数学课程标准》的理念是：观察感知、动手操作、深化理解.“向学生提供充分参与数学活动的机会，帮助他们在自立探索和合作交流的过程中真正理解和掌握数学思想和方法，获得广泛的数学活动经验”.这节课作为初三专题复习课较好地体现了《数学课程标准》的新理念，教会学生用旋转的思想去解决问题.

教学设计中比较注重数学思想的渗透与点拔，注重引领学生认识和体会数学内在的美感.如“旋转点”“基本形”等数学语言所体现的简约美；旋转变换带给学生的奇妙感觉，让学生感受数学的推力，激发学生进一步学习数学的欲望；几何画板的使用让是整个运动过程比较直观具体.练习图形的旋转过程，既让学生演示了顺时针旋转，又进一步引导学生动手实践逆时针旋转等不同方法，培养学生的思维广阔性.J