基本图形在初中数学教学中的应用研究

☉江苏省如东县茗海中学 缪晓菊

几何部分是初中数学的重要组成部分，是后期学习立体几何知识的必要前提，因此，学好初中平面几何部分知识，不仅有助于初中数学学习水平的提高，更是后期数学学习的重要保障.由于初次接触几何问题，并且在七年级接触的几何问题难度增加，使得初中几何是很多初中生学习的一个难点.在众多复杂的几何图形中，我们都可以找出它们所包含的基本图形，借助基本图形，能够将几何部分的知识衔接到一起，帮助学生寻找解题的突破口，攻克教学的难点.

一、基本图形概述

基本图形就是在初中数学课本中，描述图形定义、公理、定理的图形，如：平行四边形、圆形、直角三角形，以及具有一定代表性的例题或习题所对应的图形，例如，图1～4.

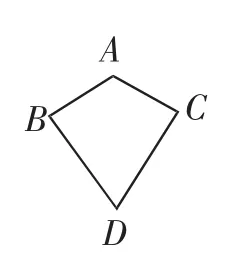
图1

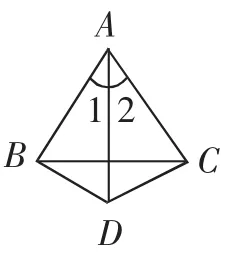
图2

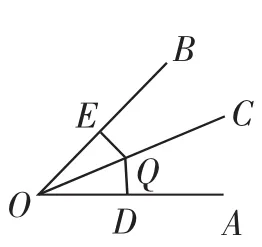
图3

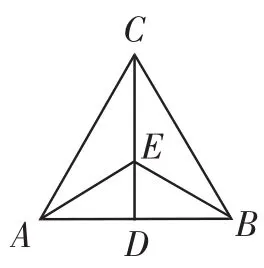
图4

如图1，已知AB=AC，BD=CD，求证：∠B=∠C.

如图2，已知DB⊥AB，DC⊥AC，∠1=∠2，求证：BD=CD.

如图3，求证：角的内部的点到两条边相等的点在这个角的平分线上.

如图4，CD是AB的垂直平分线，E在线段CD上，连接AE、BE，求证∠CAE=∠CBE.

这些习题中所涉及到的图形，也可以称之为基本图形，如果对这些基本图形加以利用，将会对数学教学的效果具有积极的作用.

二、基本图形的应用过程分析

基本图形在学生数学信息加工过程中具有重要的意义，它能够帮助学生快速地进行图形分析，寻找问题的突破口.在平时的解题过程中，我们可以将利用这种拆解复杂图形的方式，帮助学生快速完成问题的解答.

例1 如图5，在△ABC中，BD、CE分别是边AC、AB上的高，点M时BC上的中点，MN⊥DE，垂足为N，求证：NE=ND.

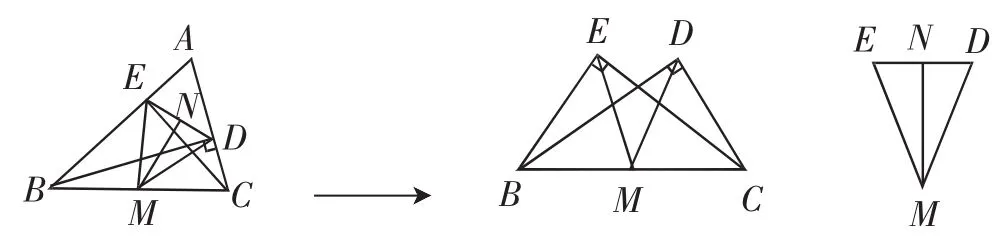
图5

问题分析：借助基本图形理念，将图中的复杂图形进行拆分，得到两个基本图形，通过第一个基本图形我们就可以明显地看出ME=MD，第二基本图形中“等腰三角形三线合一”得出NE=ND，为学生问题的解答提供了更多的有力信息.

例2 如图6，在△ABC中，AD⊥BC于点D，BE⊥AC于点E，F是AB的中点，FG⊥DE于点G.求证：∠DFG=∠EFG

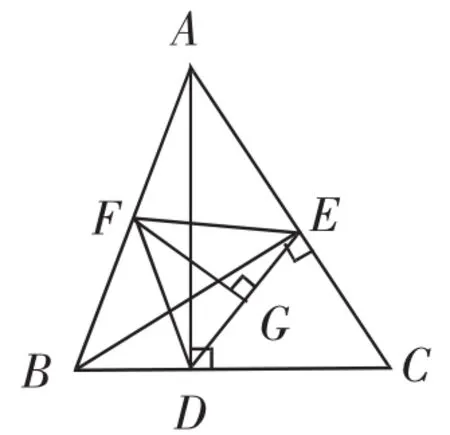
图6

问题分析：该题目的分析思路如下，根据AD⊥BC，BE⊥AC就可以得出△ABD和△ABE是直角三角形，由于F是AB的中点，就可以得出DF=AB，EF=AB，那么DE=EF.又因为FG⊥DE，最终得出∠DFG=∠EFG.为了能够帮助学生快速寻找解题信息，本题依然可以采用基本图形分解的方式，将原图转化为三个更为直观的基本图形，通过三个基本图形就可以直观地发现解题信息，求出答案.

三、基本图形在数学教学中的作用

1.承担着语言转化桥梁的作用

初中数学学习的一个重要部分就是数学语言的学习，能够灵活运用数学语言之间的转换，来表述自己的观点，寻找解题的突破口.在初中数学“平行线”部分的教学中，对学生数学语言转化的能力的培养提出了明确的要求，能够灵活完成数学语言之间的互译.例如，平行线分线段成比例定理.文字语言为：平行于三角形一边的直线，与它的两条边所截得的线段成比例.符号语言为：已知BD//CE，求证=，=，图形语言为：如图7，借助基本图形，能够使学生更加直观地理解不同数学语言之间的不同，使学生能够灵活掌握数学语言之间的灵活转化.

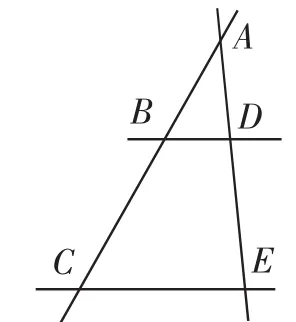
图7

2.是数学性质、定理的载体

在七年级的数学学习中，同位角、内错角、同旁内角等角的知识点非常重要，是后面研究平行问题的必要前提，也是后面数学学习的基础.借助基本图形的动态演示，能够帮助学生理解“三线八角”的定义和性质，攻克在教学中的难点.

例3 如图8，8个角的位置与数量的关系，决定了角的定义和性质，也决定着直线CD与EF之间的关系.

同位角：在直线CD、EF、AB的同侧，两角所在直线之间构成“F”状，如图8中的∠1和∠5，∠4和∠8，∠2和∠6，∠3和∠7.

同旁内角：在两条直线的内部，在第三条直线的同一边，两角所在直线之间构成“U”状，如图7中∠4和∠5.

内错角：在两条直线的内部，在第三条直线的两侧，两角所在直线构成“Z”状，如图8中∠3和∠5.

在解题中，学生如果正确使用基本图形关于定义、定理的特点，就可以快速完成解答.

例4 找出图9中的内错角.

问题分析：学生只需要结合上边所说的基本图形的载体功能，寻找“Z”状图形包含的两个角就可以快速完成求解.

3.规范学生几何解题步骤

几何证明题是初中数学必考题型，它对学生的思维能力和书写表达能力具有较高的要求，很多学生在做题中因为出现书写不规范的问题，导致出现解题错误.例如，因为题目较为简单，经常出现“易得”“易证”，和一些“跳跃性”的结论.对于初中几何证明题来说，都有固定的书写格式，它们都对应着一个或者多个推论，但是基本的格式都是一致的，因此做好基本图形逻辑推理的书写格式，是解决综合问题的必要前提.

例5 如图10，在△ABC中，点D、E分别在AB、AC上，其中BE=CD，∠1=∠2，证明△ABC是等腰三角形.

图8

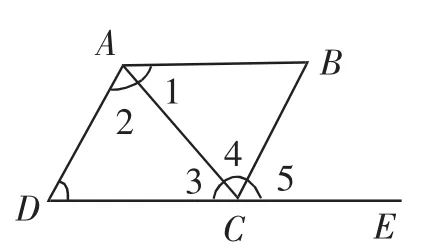
图9

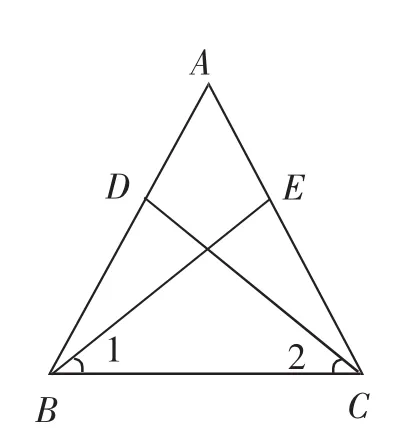
图10

问题分析：将原有图形拆分为基本图形，要证明原题只需要证明两个基本图形就可以，将两个基本图形的逻辑证明推理组合起来就成为了这道题整个的证明过程.需要注意的是，在两个图形分析中，有的逻辑推理就是下一个图形推理的结论，这样这样的情况只需要书写一次即可.在△ECB和△DBC中，BE=CD，∠1=∠2，BC=CB，所以△ECB≌△DBC，所以∠ECB=∠DBC，所以AB=AC，所以△ABC是等腰三角形.

4.构造基本图形，解决复杂数学问题

在解决数学几何问题的时候，通过构造基本图形的方法来寻找解决综合问题的突破口，是我们常用的解题方法，我们通过添加辅助线、割补图形等方法来完成基本图形的构造，然后借助基本图形的性质来完成求解.

四、基本图形在教学设计中的应用

本文以等腰三角形的判定部分的教学内容为例，对基本图形在教学中的应用方法做简要阐述.该章节的教学重点在于探索和掌握等腰三角形的判定方法.

1.引导思维阶段

在该部分的教学设计中，引入折纸实验，通过实验探究，激发学生的学习兴趣和思考欲望.首先，教师在多媒体上展示两组折纸图片，如图11，学生根据视频所示进行来动手折纸.认真观察纸张折合部分三角形的特征，它们是否是等腰三角形？它们的角之间有什么样的特殊数量关系？

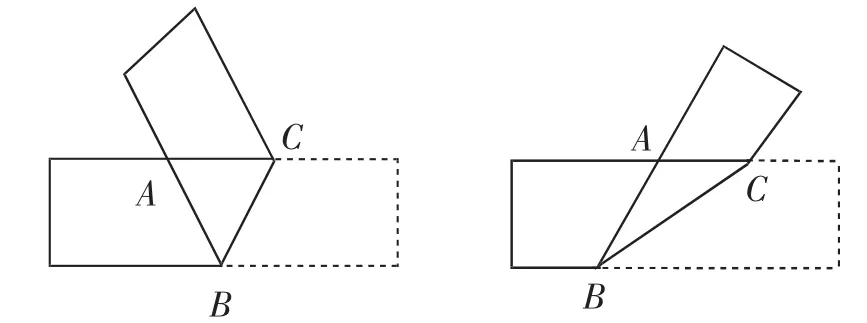
图11

2.定理论证阶段

如图12，在△ABC中，∠B=∠C，说明△ABC是等腰三角形.我们如何能够构造出一个以AB和AC为对应边的全等三角形呢？

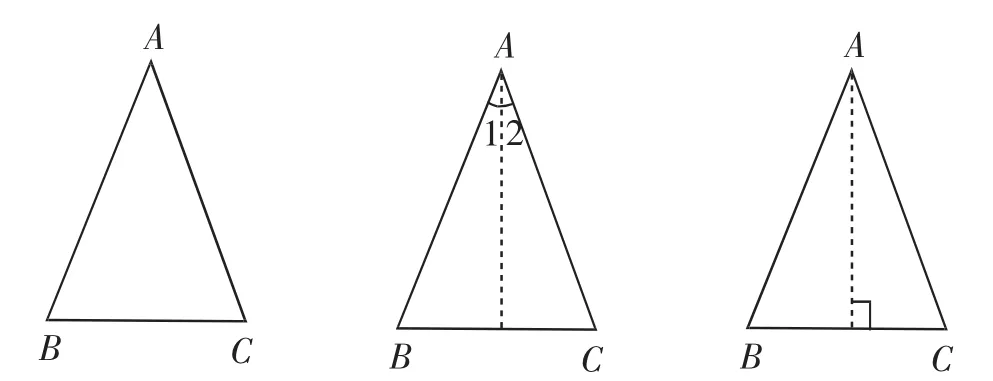
图12

学生思考：通过作∠A的平分线，根据AAS定理就可以证明出AB和AC为对应边的三角形全等，通过A作BC的垂线，利用ASA定理也可以证明AB和AC为对应边的三角形全等.

教师提出问题：如果作BC的中线，是否能够证明AB和AC为对应边的三角形全等？

3.定理强化阶段

在这一阶段，主要是运用基本图形，帮助学生梳理语言、强化书写，提高学生文字语言、图形语言、符号语言之间的灵活转化能力.

首先，借助简单的问题，帮助学生熟悉“等角对等边”，认识常见的基本图形.

例6 说明图中共有几个等腰三角形.如图13所示在△ABC中，已知∠A=36°，∠ABC=72°，BE是∠ABC的角平分线.

（1）如图14，DE∥BC；

（2）如图15，CD平分∠ACB，连接DE；

（3）如图16，EF为∠BEC的角平分线，FG为∠EFC的角平分线.

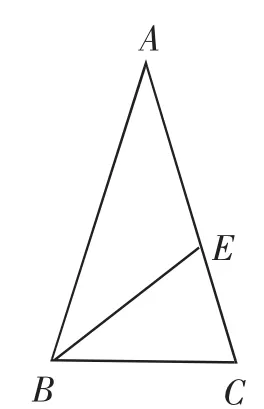
图13

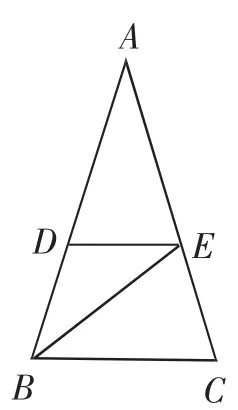
图14

图15

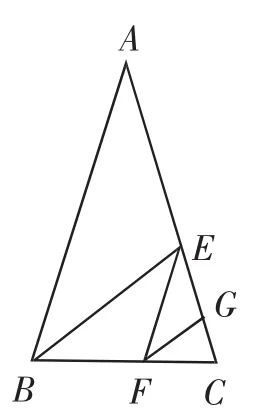
图16

其次，让学生体会从复杂图形中分离基本图形，体会基本图形的应用思路，鼓励学生在解题事件中应用基本图形.

图17

图18

例7 如图17，在△ABC中，BP和CP为∠ABC和∠ACB的角平分线，MN∥BC，证明：MN=BM+CN.

例8 如图18，BD是∠ABC的角平分线，CD平分△ABC的外角，DE∥BC，证明：EF=BE-CF.

五、小结

几何部分是初中数学的一个重点也是难点，很多学生对几何问题的求解是望而却步.其实，任何几何都是由基本图形构成，只要抓住了基本图形，在复杂的几何问题都可以迎刃而解.另外，通过基本图形的学习，能够帮助学生更好地理解相关的几何知识，提高数学学习的效果.J