一题多解需谨慎 分层递进是良策*

☉江苏省无锡市锡山高级中学匡村实验学校 周荣伟

在当前初一、初二的数学课堂上经常会看到这样两种现象：新授课上为了追求所谓的教学深度，简化知识的发生过程，忽视例题的基本方法，更多关注的是一题多解、一步到位（美其名曰：深度学习、与中考接轨！）；但是到了单元习题课、章节复习课、期末复习课、乃至初三中考复习课上却依然停留在回忆式的习题讲解上，除了提高解题的熟练度，方法并没有任何更新.笔者认为，导致这两种现象频发的主要根源是对一题多解教学理解的偏失.本文以苏科版义务教育教科书数学八年级上册的一个习题为例，谈谈如何基于分层递进开展一题多解教学，以真正提高新授课、习题课以及复习课的教学效益.

一、题目呈现

已知：如图1，在平面直角坐标系中，△OAB三个顶点的坐标分别为O（0，0），A（2，4），B（6，2）.求△OAB的面积.

图1

图2

二、基本解答

视点1：这是八上第5章《平面直角坐标系》第5.2节平面直角坐标系第二课时（新授课）的内容，课标要求是把一些简单图形置于平面直角坐标系中，探索点的坐标与线段长度之间的转化，从而进一步感受“数形结合”的数学思想.基于此，应该引导学生得出以下两种常用的面积分割法.

解法1：如图2，过点A作DC⊥y轴，垂足为点C，过点B作DE⊥x轴，垂足为点E，两条线相交于点D，则四边形OCDE是长方形.（注：苏科版义务教育教科书中《矩形》要到八年级下册才出现）

解法2：如图3，过点A作AF⊥x轴，垂足为点F，过点B作BE⊥x轴，垂足为点E，则四边形AFEB是直角梯形.

视点2：八上第6章《一次函数》的单元复习课，课标要求是能根据一次函数的图像，利用待定系数法确定一次函数的表达式，在经历用一次函数解决问题中增强应用意识，并逐步加深对函数思想的理解.基于此，应该引导学生得出以下两种常用的函数解析法：

图3

图4

解法3：如图4，过点A作AF⊥x轴交直线OB于点G，垂足为点F，过点B作BE⊥x轴，垂足为点E.首先，利用待定系数法分别求出直线OA的解析式为y=2x，直线OB的解析式为y=x，然后再由A（2，4）得出G（2，），从而求出线段AG=AF－GF=4－=.

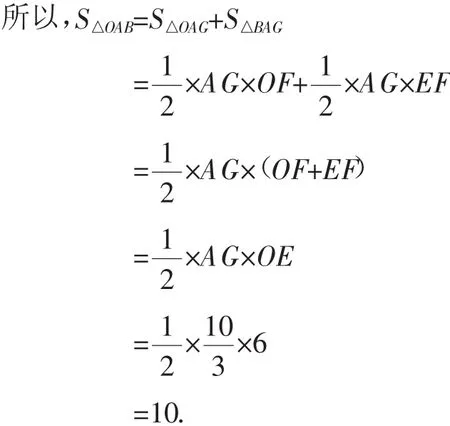
解法4：如图5，延长线段BA交y轴于点H，过点A作AC⊥y轴，垂足为点C，过点B作BK⊥y轴，垂足为点K.首先利用待定系数法求出直线AB的解析式为y=-x+5，然后再求出H（0，5），从而得出线段OH=5.

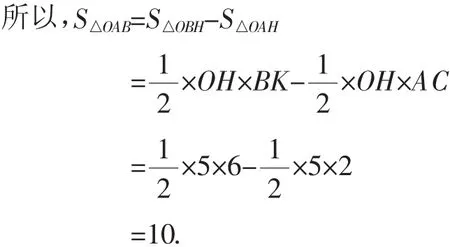
视点3：苏科版义务教育教科书数学八年级上册的目录依次为：第1章《全等三角形》，第2章《轴对称图形》，第3章《勾股定理》，第4章《实数》，第5章《平面直角坐标系》，第6章《一次函数》，因此到期末复习课时，又可结合前面的第1章《全等三角形》和第3章《勾股定理》的相关知识，通过判断三角形的形状再加以解决.基于此，应该引导学生得出以下两种常用的形状判定法.

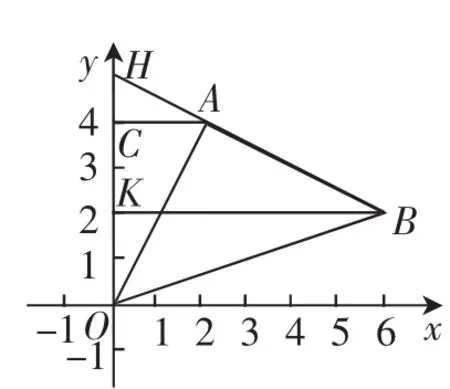
图5

图6

解法5：如图6，过点A作AC⊥y轴，垂足为点C，过点B作BD⊥AC，垂足为点D.

在△OAC和△ABD中，

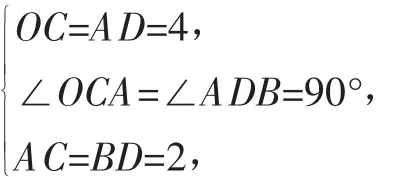
所以△OAC≌△ABD（SAS）.

因为AC⊥y轴，所以∠ACO=90°.

所以∠OAC+∠AOC=90°，所以∠OAC+∠BAD=90°.

所以∠OAB=90°，即△OAB是直角三角形.

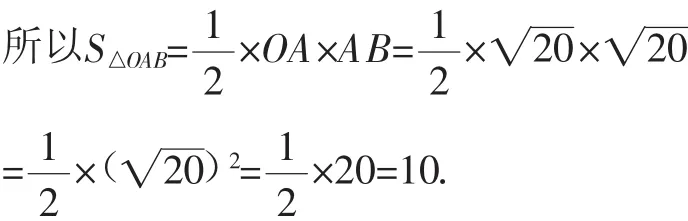
（注：苏科版义务教育教科书《二次根式》要到八年级下册才出现，这里用的是平方根的意义求解，下同）

所以OA2+AB2=OB2，

由勾股定理逆定理可知，∠OAB=90°.（下面的解法同解法5）

三、教学反思

1.一题多解的教学起点应该源于学生的认知现实

在当前的初中数学课堂教学中，无论是基于学生的想法，还是基于老师的预设，一题多解教学似乎是课堂教学的标配，某些学校（或各类评优课）甚至把它纳入到课堂评价的范畴.因为一题多解教学确实能够帮助学生夯实基础，提高学生的认知能力，同时也可以培养学生思维的发散性和灵活性，提高学生的创新能力.但我们需要关注的是一题多解的教学起点：学生的认知现实.一题多解教学必须要在学生对有关的知识和技能熟练掌握的基础上进行，如果学生对有关的知识和技能没有熟练掌握，就谈不上灵活运用，谈不上纵向、横向联系，也就不能进行一题多解教学.相反，学生对基础知识掌握得越深刻，越透彻，基本技能越娴熟，越灵活，一题多解教学效果就越好.本课时的教学目标是探索点的坐标与线段长度的转化.因此，对于该题的解答，比较符合学生认知现实的应该是面积分割法，即解法1和解法2.也就是说，在新授课上，该题的一题多解教学更多的应该体现在“面积分割”方法的多样性上，而不是急于用形状判定法，即解法5和解法6，这样反而会导致因其他难点（形状判定）而淡化课时目标.

2.一题多解的教学节奏应该基于课标的分层递进

《义务教育数学课程标准（2011年版）》在第一部分前言的课程基本理念中明确指出：“课程内容的呈现应注意层次性和多样性.”第四部分实施建议的教材编写建议中也提出：“重要的数学概念与数学思想要体现螺旋上升的原则.”这就要求我们要树立与新课程相适应的教学观：在不同学习阶段重复呈现特定的学科内容（也包括解题方法），同时利用学生日益增长的心理的成熟性，使学科内容不断拓展与加深——分层递进，螺旋上升.因此，一题多解的教学节奏也应该基于课标要求，从“一步到位”向“分层递进”转变.分层递进的基本策略主要有三条：一是教师的教要适应学生的学，学生的学是有时空差异的，教师的教也要有分层差异；二是每一个学生都有充分发展的潜能，要促进他们在原有基础上得到较好的发展；三是学生之间的差异是一种可以开发利用的教育资源.笔者认为，对于求解此类三角形面积问题，解法1和解法2比较适用于新授教学课，解法3和解法4比较适用于单元习题课，解法5和解法6则适用于期末复习课，而到了初三中考复习课，应该是在复杂图形背景下对上述6种解法进行综合运用，如2017年江苏苏州中考压轴题第28题第（3）小题：

如图7，二次函数y=x2+bx+c的图像与x轴交于A、B两点，与y轴交于点C，OB=OC.点Q在函数图像上，CD∥x轴，且CD=2，直线l是抛物线的对称轴，E是抛物线的顶点.

（1）求b、c的值.

（2）如图7，连接BE，线段OC上的点F关于直线l的对称点F′恰好在线段BE上，求点F的坐标.

（3）如图8，动点P在线段OB上，过点P作x轴的垂线分别与BC交于点M，与抛物线交于点N.试问：抛物线上是否存在点Q，使得△PQN与△APM的面积相等，且线段NQ的长度最小？如果存在，求出点Q的坐标；如果不存在，说明理由.

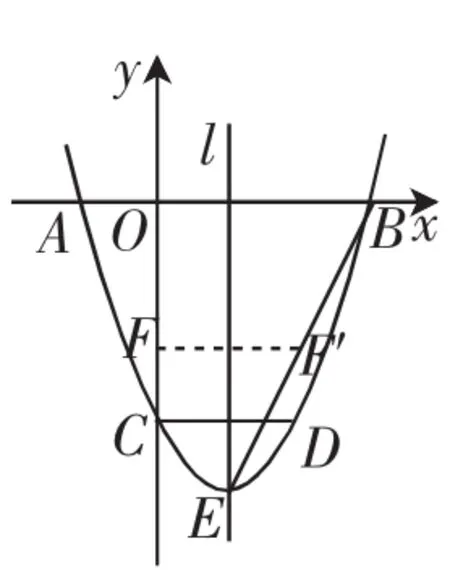
图7

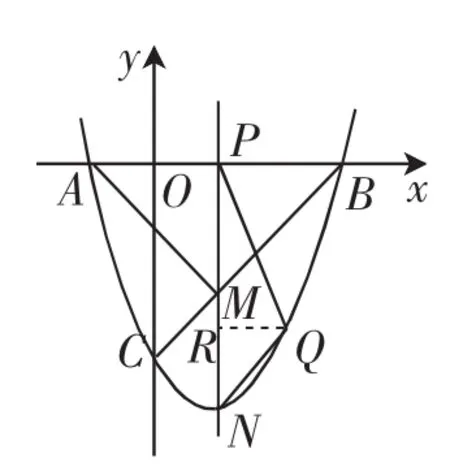
图8

3.一题多解的教学追求应该终于数学的整体理解

在学生了解多种解题方法之后，学生的解题思维不能到此完结，因为学生此时对各种解题方法的认识还不是非常深刻：哪些是一般的解法，哪些是创新的巧法，哪种是最简便的解法等，这些都需要逐步引导学生自己去思考，进一步去认识.复习课需要重复但又不能简单的重复，需要知识技能再认识，思想方法再升华，活动经验再积累，核心素养再落实，应重而不复.比如，在初三中考复习阶段，把本例的条件“B（6，2）”改为“B（5，2）”，那么通过判断三角形形状的解法5及解法6就行不通了.而对于利用面积分割的解法1及解法2，其实是源于初一年级（甚至在小学阶段）的网格图，也不应该是初三中考复习的教学追求.那么对于初三年级的孩子，该题的教学追求究竟是什么呢？不妨先看2017年苏州中考第28题第（3）问的略解：

设点P坐标为 （n，0），则PA=n+1，PB=PM=3－n，PN=－n2+2n+3.作QR⊥PN垂足为R.

因为S△PQN=S△APM，

当点Q在直线PN的左侧时，Q点的坐标为（n－1，n2－4n），R点的坐标为（n，n2－4n），N点的坐标为（n，n2－2n－3）.在Rt△QRN中，NQ2=1+（2n－3）2，所以n=时，NQ取最小值.此时Q点的坐标为 （， －）.

当点Q在直线PN的右侧时，Q点的坐标为（n+1，n2－4），同理，NQ2=1+（2n－1）2，所以n=时，NQ取最小值.此时Q点的坐标为 （，－）.

“一览众山小”，站在初三中考要求、课标要求、以及学生数学核心素养要求的高度来审视此类三角形面积求解问题，强化学生函数建模能力的解法3和解法4是更容易揭示问题的本质结构的最优解法.这就相当于是在认知与元认知两个层面都有所提升、有所收获，这应该是该题一题多解的教学追求.

总之，一题多解的教学，应根据学生的年龄特征与知识积累，在遵循科学性的前提下，宜采用分层递进、螺旋上升的原则，而且在深度、广度等方面都要有实质性的变化，即体现出明显的阶段性要求.所以，如果真正能够做到把一题多解的教学作为一个分层递进的整体来思考，通过新授课首呼、习题课中联、复习课尾应，那么，必定可以在学习数学的过程中掌握“四基”，在应用数学的过程中提高“四能”，最终在学习与应用数学的两个过程中整体达成“六核”的数学学科核心素养目标.