遵循正确策略，科学探寻规律——以一道中考几何规律题的探究为例

☉浙江省宁波市鄞州区云龙镇中学 曹世贤

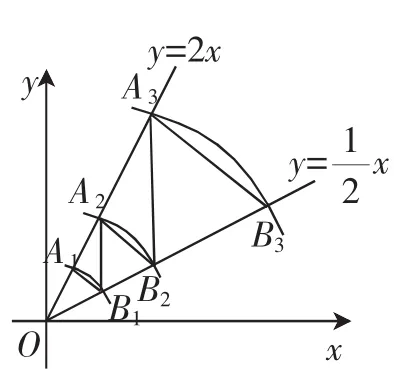
图1

几何规律探寻题在近几年中考中出现的频次很高，该类问题一般以平面直角坐标系为背景，结合大量的文本操作，以考查学生对于图形认识，信息提取，规律探究的能力.本文将以一道中考几何规律探寻题为例开展思路探究，并进行相应的学习思考，以期对读者的学习带来一定的启示.

一、试题呈现及简析

例题 （2018年山东威海市中考卷第18题）如图1所示，在平面直角坐标系中，点A1的坐标为（1，2），以点O为圆心，以O长为半径画弧，交直线y=x于点.过B点1作B1A2∥y轴，交直线y=2x于点A2，以O为圆心，以OA2长为半径画弧，交直线y=x于点；过点作BA∥y轴，23交直线y=2x于点A3，以点O为圆心，以OA3长为半径画弧，交直线y=x于点；过B点作BA∥y轴，交直线y=2x于334点，以点O为圆心，以O长为半径画弧，交直线y=x于点B4，…按照如此规律进行下去，则点B2018的坐标为__________.

简析：上述题目是一道典型的平面直角坐标系中的规律探寻题，题目涉及到作平行线、画弧等操作，考查了扇形、三角形、相似、点坐标等知识，是数形结合思想、归纳转化、模型思想的综合考查.解答本题目除了需要理解题目中的作图过程，还需要结合几何性质来确定关键点的坐标.其中结合问题条件确定点A1、B1的坐标是问题探究的起点，然后以上述两点为基础来总结后续点获得的方法，形成规律，归纳通解式.

二、试题求解过程探究

1.识图读题，提炼基本图形

对于一般含有大量文字信息的几何题，都是采用“先读题，再读图”的策略，即从题目的文本信息入手，理解题意，再对几何图形进行探究，但这样的解题策略对于几何规律探究而言并不完全适用，因为探究题一般结合了必要的操作过程，如果首先读取文本信息，很难获得有效信息.在此建议首先观察图像，读取图形中的典型特点，初步探寻其中可能存在的性质.对于本题目从几何图形来看，在直角坐标系中存在两条正比例函数直线，多条平行于y轴的直线，以及两类常见的图形，扇形和三角形.显然，通过观察图像可以获得较为直观的几何认识，借助直角坐标系研究图形的性质对于后续的规律探究是十分有利的.然后再详细地阅读题目文本，提取其中的关键信息，例如“以点O为圆心，以OA1长为半径画弧，…过B1点作B1A2∥y轴，交直线y=2x于点A2，…按照如此规律进行下去”，文本中主要有两个关键作图步骤，一是以原点O画圆弧，二是过标有序号的点B以规律长线段作y轴的平行线.如果按照这样的方式进行持续作图，图中必然会出现较多的平行线、同心弧，其中的边长和角度之间也存在一定的关联.

2.图文对应，确定初始数据

根据题目中所描述的作图过程，以及初始点坐标，可以获得两个较为明显的数据：根据点A1的坐标（1，2），可求得OA1=；由O长画圆弧，则O=O=，而根据位于直线y=x上可以设出点的坐标为 （a，a）.除了上述的线段长以及坐标关系没有更多可以提炼的数据，因此其他数据的获得需要结合作图过程以此来生成，另外文本中关于平行线的作法可以获得相应的坐标关系，如B1A2∥y轴，则可以推得B1的横坐标与A2的横坐标相等，在求解时可以适度地将这些数据标注在对应的点和线段上，从而明确哪些为已知条件，哪些是可推得的信息，哪些是待探究的信息.这样可以准确把握后续问题的探究方向，避免“走弯路”.

3.适度拓展，推导衔接数据

根据上述的几何关系和求出的初始数据，可以通过简单的计算来获得一些具有衔接性的拓展数据，如点O，点的坐标 （a，a）可以建立关于参数a的求解方程a2+ （a ）2=（）2，解得a=2，可得B（12，1）；进一步根据xB1=xA2=2，以及点A2位于正比例函数y=2x上可以求得点A2的坐标为（2，4）.此外结合几何的相似原理可知图像中存在一些相似图形，如其中的扇形OA1B1、OA2B2、OA3B3互为相似，则根据相似性质可知其中的边OA1、OA2、OA3…OAn，OB1、OB2、OB3…OBn之 间必然存在一些比例关系，利用这些推导的数据可进一步开展研究.

4.深度关联，猜想通解规律

由上述数据可以进一步推导后续点的坐标，B2（4，2）、A3（4，8）、B3（8，4），考虑到xBn=OBn·cosα，yBn=OBn·sinα （α为直线y=x与x轴的夹角 ） ，=O·cosβ，=OAn·sinβ（β为直线y=2x与x轴的夹角），可知点坐标之间的比例关系与线段之间的比例关系相同，因此根据OA1∶OA2∶OA3=1∶2∶4，OB1∶OB2∶OB3=1∶2∶4可猜想OA1∶OA2∶OA3∶…∶OAn=1∶2∶4∶…∶2n-1，OB1∶OB2∶OB3∶…∶OBn=1∶2∶4∶…∶2n-1，则点坐标之间也必然存在这样的比例关系，可以猜想点B的坐标有如下推导公式：xBn=xB1·2n-1=2n，yBn=yB1·2n-1=2n-1，于是可以猜想点Bn（2n，2n-1）.

5.形成数系，合理检验通式

与点B的坐标通式猜想相同，可以获得点A的推导式An（2n-1，2n），然后建立相应的点系，如点A系：A1（1，2）、A2（2，4）、A3（4，8）；点B系：B1（2，1）、B2（4，2）、B3（8，4）.这种推导方式属于不完全归纳，是否适用于一般情况还有待论证，可以结合几何坐标以及相关性质进行进一步点的计算，然后与通式的结果进行比较.如求得点B3（8，4）后可以继续取n=4，利用通式可得B4（16，8），而根据图像中的规律可知xA4=xB3=8，点A4位于y=2x上，则yA4=16，即A4的坐标为（8，16），画弧可得点B4的坐标，设其为（b，b），根据半径相等可得b2+ （b ）2=82+162，解得b=16，所以点B4的坐标为（16，8），上述采用的是函数解析法的求解方式，同样可以获得点B4的坐标，且与猜想的通式结果相一致，因此坐标通式是正确的，使用通式Bn（2n，2n-1）可以计算出点B2018的坐标为（22018，22017）.

三、试题求解的感悟

1.遵循特定策略，挖掘信息条件

中考中的几何规律探寻题，除了会给出具有规律性的文字描述外，还会配合对应的几何图像，而对规律的探寻需要以分析数据变化为主，而这些数据的变化充分体现在直观的图像上，如上述点坐标之间的比例关系由几何线段之间的长度比例来体现，因此对于结合了直角坐标系的坐标规律探寻题需要从文本、图像两个方面来完成信息提取，图文配合挖掘隐含条件.另外在解题时需要采用正确的解题策略，遵循“识图—读文—对应”的分析步骤，深刻认识图形特征，把握初始数据，图文对应理解问题的作图过程，获得几何元素之间的隐含联系，会后续的思路分析，猜想证明作基础.

2.多维数据提取，合理实施猜想

数学规律的探寻是建立在对问题信息条件的理解之上，即首先理解问题的作图过程，掌握规律的形成方法，然后懂得如何使用文中方法获得后续的数据.因而在剖析问题时，需要充分提炼题干的关键信息，如几何的性质条件、基本数据，然后对提炼的信息进行整理，从中获得利于后续思路推导的有用信息.对于与问题不相关的信息可以适当的删减，如上述考题中可以提炼出几个相似的三角形，但考虑到线段的边长难以获得，因此可以将其删除.数据的提炼是为后续的猜想作准备，在该环节需要充分结合几何性质，深入分析信息之间的关联性，可以将对应的数据放入直观的图像中，结合几何线段、角度来分析，参考数学上数形结合的方式进行.几何规律探寻题是特定情景下的规律探究，虽然信息给出的形式呈现多样化，但同时也为问题解决提供了多种途径，进行图文配合，多维度提炼数据是解题的有效方法，将特定数据放置在具体的图形中，更能检验其可靠性，为合理猜想铺平道路.

3.科学验证猜想，上升理论高度

规律探寻题的另一个关键环节是对猜想的证明，该过程相对而言较为复杂，但却是检验猜想必不可少的过程.在具体的实施中可以采用多思路验证的方式，即从不同的角度来拓展数据、验证数据，如几何探寻题可以参照题干方法来进一步推导数据，然后与猜想所获得数据相对比，从而完成结论的论证过程，上述考题就是利用几何性质来进行数据拓展与验证的.结论验证的过程是多样的，但必须遵循一定的原则，即论证过程必须具有逻辑性、严谨性和一般性，不能采用循环自证的方式，而应是不同理论指导下的科学推导.对于几何规律探寻题需要充分利用几何中的性质定理，按照科学的证明思路来完成推理，确保结论的获得是建立在理论基础之上.总之，猜想是对问题特征的感性思考，结合理性的推理验证才能上升到理论高度，从而获得最终答案的通解.

四、结束语

几何规律探寻题是中考数学的重点题型，虽然其难度梯度差别较大，但其中存在一定的推理方法，本文所论述的是其中一种较为有效的解题策略——把握几何特征，提炼文本信息，图文配合推理，科学严谨论证，依照该思路开展规律探究，可实现问题的高效求解.