答疑有法，智慧成长——初中数学理答技巧分析

☉江苏省无锡市第一女子中学 项 菲

学生在遇到难题时能够及时请教老师是一种优良的本能反应，教师及时帮助学生解决疑难能够起到多方面的效应.学生带着问题请教老师是其内在需求驱动的表现，教师为学生诊断思维障碍则是了解学情的大好良机，这相互之间的情感交融能更好地促进学生心智的觉醒以及智慧的生成.

教师在回答学生疑问之时能够采取的形式很多，但终究必须遵循帮助学生学会思考并形成智慧的这一原则.笔者教学中的一个实例如下.

学生疑问：已知A（2，-3），B（4，-1），C（a，0），D（a+3，0）在平面直角坐标系内，当a为何值时能令四边形ABCD周长最小？

帮助学生解决这一问题的整个过程如下.

一、以退为进，降低探索入口

图1

师：大家先来看看这个问题：已知A（2，-3），B（4，-1），C（a，0），则a为何值时能令△ABC周长最小？此题会做吗？

生1：这是求CA+CB最小的几何问题，如图1所示，关键是x轴上的点C的横坐标.可以先找出A（2，-3）关于x轴的对称点A′（2，3），然后连接A′B，可得直线A′B的解析式为y=-2x+7，令y=0，得x=，联系初二学习过得内容可知，当a=时，CA+CB最小，AB的长是一定的，因此此时△ABC周长最小.

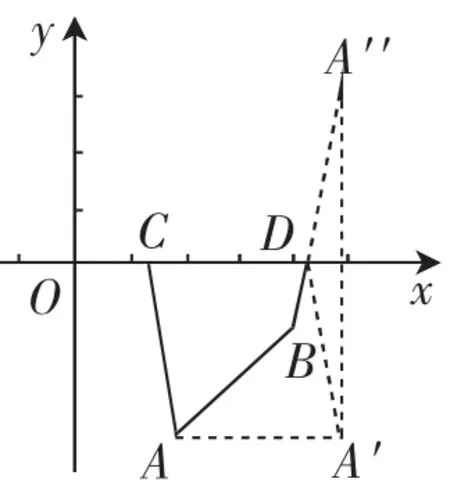
图2

生2：（观察很久）：C点应该满足CA′=CA和C、A′、B三点一线才可以.

师：观察得很仔细，你的结果或许有用.我们回过头来看看你们先前的问题，四边形ABCD的周长是AB+BD+DC+CA，DC为长是3的位于x轴的动线段，AB为定线段，因此，问题直接转化成了AC+BD最小即能令四边形ABCD周长最小，两定两动求距离和最小这一问题可以转化成两定一动的问题吗？（如图2中的实线部分四边形ABCD）

给几位学生一定的思考与讨论时间后，有学生发言了.

生3：如果将图2中的AC向右平

通过采用现代的组合砂轮工具，磨削工艺和抛光工艺能够同时实现。在展成法磨齿工艺中，组合砂轮工具得到了充分地使用。

移到A′D的位置，求AC+BD最小就意味着求x轴上一点D并使A′D+DB最小这一问题了.具体如下：把点A（2，-3）右移3个单位得A′（5，-3），作A′关于x轴的对称点A′′（5，3），连接A′B，则A′B和x轴的交点就是我们要求的，而且点D确定之后点C也因此确定了.

师：能说说理由吗？

生3：根据平移知识可得AC=A′D，A′、A′′关于x轴对称，所以A′D=A′D，即AC=A′D，由线段基本性质得A′D+DB最小，则有AC+DB最小，因为AB、CD的长都为定值，因此四边形ABCD的周长此时是最小的.

师：怎样求a呢？

生4：首先求出直线A′′B的解析式y=4x-17，令y=0，得x=，所以a+3=，则a=.

师：还有其他办法吗？

生1：他是平移AC来转化解题得，平移DB也行，我来画图（图3）.

其他学生在这启发下又画出了图4和图5并进行了理由说明（略）.

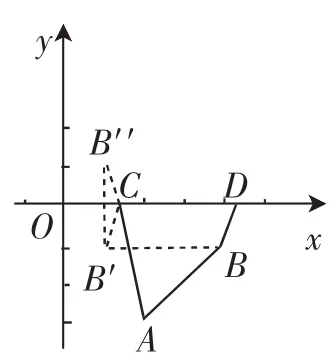
图3

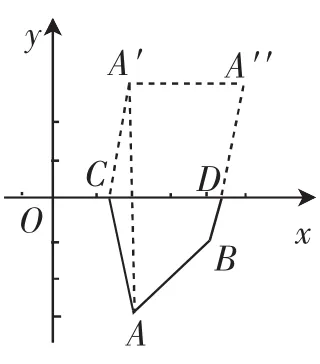
图4

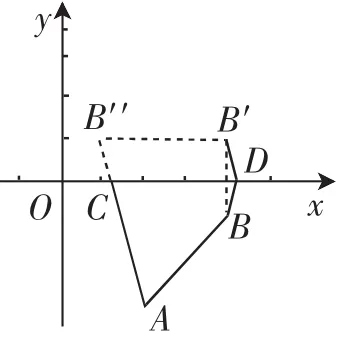
图5

教师将学生的疑问进行转化并促进学生自主思考就好比为学生培育了智慧生长的土壤，教师在这一过程中应启发学生这一思维主体的觉醒并使其心智得到启发.回顾此题的思考与解决，图1中的AC=A′C，A′、C、B三点共线这两个本质条件的灵活应用正是学生在智慧生成的过程中获得的.

二、启思诱导，变式中拓展思维空间

问题解决到这一阶段也已经算解决了，不过细看C、D两点的位置不难发现本题仍具有一定的可变性，于是笔者提出这样一问：假设C、D位置发生了变化，你们能不能进行新题的改编呢？

学生在另一个课余时间进行了改编题目与解答的展示.

题目1：已知A（2，-3），B（4，-1），C（0，a），D（0，a+3）在平面直角坐标系中，则a为何值时能令四边形ABDC周长最小？

略解：如图6，作点A关于y轴的对称点A′并将之往上平移3个单位可得A′′（-2，0），连接A′′B与y轴相交于D，根据原题的解答可知此时四边形ABDC的周长最小.

设直线A′′B的解析式为y=kx+b，将A′′（-2，0），B（4，-1）代入可得y=-x-.令x=0得y=-，所以a+3=-，即a=-.

题目2：已知A（2，-3），B（4，-1），C（0，a），D（b，0）在平面直角坐标系中，则a、b为何值时能令四边形ABDC周长最小？

图6

图7

略解：如图7，作点A关于y轴的对称点A′（-2，-3），作点B关于x轴的对称点B′（4，1），连接A′B′交x轴于点D，交y轴于点C，则四边形ABDC周长此时最小.

笔者追问：有什么理由说它周长此时最小呢？

生1：在x、y轴上分别取不同于D、C的点D1、C1，则有BD+DC+CA=B′D+CD+CA′=B′A′＜B′D1+D1C1+C1A′（线段B′A′的长小于折线断BD1C1A′的长），因此四边形ABDC周长最小.

生2：设直线A′B′的解析式为y=kx+b，将A（′-2，-3），B（′4，1）代入后可得y=x-，令x=0得y=-，令y=0得x=，则当a=-，b=时，四边形ABDC周长最小.

生3：假如将C、D两点的坐标改成C（a，0），D（0，b），由图8可得，当a、b不等于0时，四边形ABDC的周长取不到最小值.

生4：我们也有将点D坐标用（a+3，0）或（0，a+3）来表示的想法，不过在符合条件的a的值上感觉有难度，是不是有什么办法可以解决？

笔者在学生展示自编新题与解答过程中也适时进行了追问，学生在整个过程中展现出了流畅的思路，感受到了学生在此题的探索中已经逐步学会了运用变化的观点来进行可变图形的观察，深知学生对课本知识的本质以及思维的入口已经很好掌握与定位，欣慰于学生内在驱动力不断生成的同时也对学生提出了更高的要求，请学生对问题的新型解法进行探索.

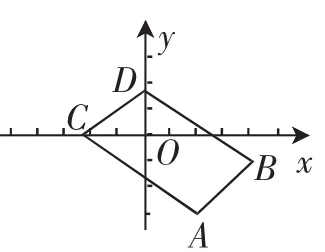
图8

三、思路突破，探求新解法

用题目2的解法来解决生4所提出的问题确实是行不通的，因为C，D坐标中的a、b并不能满足b=a+3，也就是说A′，C（0，a），D（a+3，0），B′或A′，C（a，0），D（0，a+3），B′不可能共线.

师生又作探讨：设C（0，a）、D（a+3，0），根据两点间距离公式得：AC+BD=，此时用代数方法求AC+BD的最小值无法解决，是否能从式子的特征结构来构造符合等式结构的图形最终解决问题呢？大家可以再试试.

这几个学生在又一个空余的时间呈现了他们的再次解答：设a+3=x，则1-a=1-（x-3）=4-x，此时AC+BD=

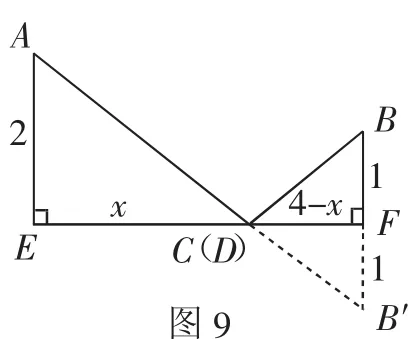
图9

根据这一等式特征可以构造图9并观察得出：问题最终化归为在长是4的线段上找一点C（D）并使AC+BC最小，作点B关于直线EF的对称点B′，连AB′交EF于C，则点C即为所求，由△AEC∽△B′FC可得：2∶x=1（∶4-x），x=，由a+3=时，折线CABD的长最小.

生2受到启发并画出图10进行了解答.设C（a，0），D（0，a+3），根据两点间距离公式得AC+BD=.设a+4=x，则2-a=2-（x-4）=6-x，所以AC+，根据等式特征构造出图11并可观察出，当C、D重合且A、C、B三点共线时，AC+BD最小，由△AEC∽△BFC可得，4∶x=3（∶6-x），x=，由a+4=，得a=-，则a+3=，即当C（-，0 ），D（0，）时，折线CABD最短.

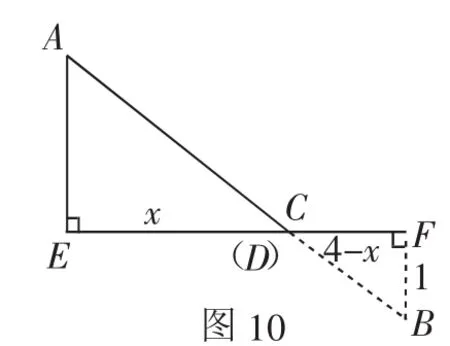
图10

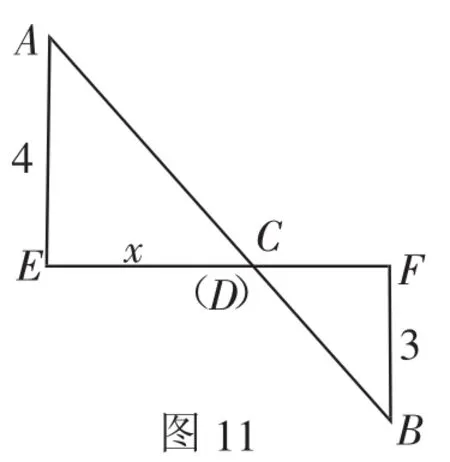
图11

很显然，在C（0，a），D（a+3，0）或C（a，0），D（0，a+3）的条件下求四边形ABDC周长最小时a的值对于学生来说是解决不了的，但学生在原题的深度讨论与探索中所获得的智慧与感悟却是永存心间的.

四、反思总结，引领学生智慧成长

1.引领学生在化归中智慧成长

学生往往因为已有知识与问题结论之间无法形成联系的通道而令自己的思维受阻，化归是此时打破思维僵局并促进学生智慧生成的有效办法，因此，教师在解答学生疑惑时应专注于启发学生如何思考，使学生能够在不断的引导与启发下将已有知识与有待解决的问题形成对接并顺利突破.

2.引领学生在变化中智慧成长

很多教师在实际教学中往往止步于问题的解释、思路或结果，对于问题所能产生的价值却关注甚少，这对于学生的智慧成长来说是消极的.教师在解决学生疑惑时应看到问题背后隐藏的本质并引导学生进行条件、结论等的变式，使问题在不断变化中衍生出更多的内涵并因此促进学生智慧的生成.

3.引领学生在另辟蹊径中智慧成长

一些暂时无法解决的问题在另辟蹊径后往往会令学生学习兴趣倍增，也能促进学生能力的超越并使学生在再发现、再创造出获得更加光亮的思维火花，学生在这些可变性、可解性问题的探索中往往能够迸发、生成新智慧.H