一道中考试题的“前世、今生和拓展”

☉山东省博兴县教学研究室 刘克光

☉山东省邹平县黄山实验初中 由学芹

我们有幸参加了本市2018的中考数学命题工作.试卷中第19题如下：如图1，在矩形ABCD中，AB=2，BC=4，点E、F分别在BC、CD上，若AE=，∠EAF=45°，则AF的长为___________.

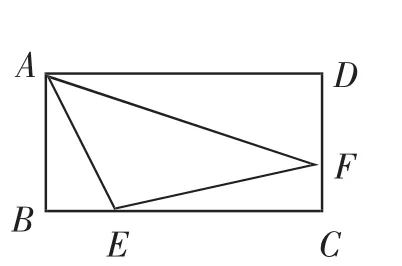
图1

现把本试题命制的过程、思考、感悟与大家分享如下.

一、试题的前世

第19题来自新课标人教版九年级数学上册第60页的课本例题：如图2，E是正方形ABCD中边CD上任意一点，以点A为中心，把△ADE顺时针旋转90°，画出旋转后的图形.

例题分析1：旋转变换的特征有三个，对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等.

例题分析2：正方形的特征有三个，正方形的各边都相等，恰好便于旋转后边的重合；正方形的内角等于90°，恰好为本题中的旋转角；经过旋转后所得三角形的边BF，恰好在正方形的边BC所在直线上.

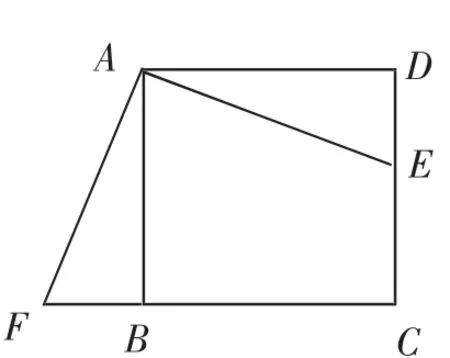
图2

例题分析3：正方形的特征决定了它本身是考查旋转变换知识的很好载体.同样正三角形等正多边形也具有同样的特征.

二、试题的今生

从此问题出发，通过固定点E的位置，在正方形内部作∠EAF，使其等于45°而得以下问题：

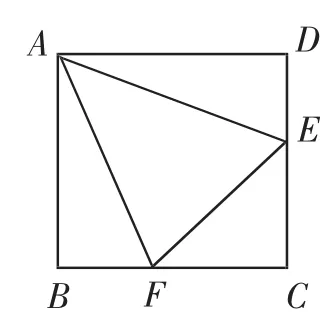
图3

题1：如图3，正方形ABCD的边长为2，点E、F分别在CD、BC上，若AF=，且∠EAF=45°，则AE的长为_________.

此问题的突破口就是把△ADE顺时针旋转90°，得到“前世”的基本图形（如图4），利用∠BAF+∠DAE=45°， 证 明△AEF≌△AMF，得到MF=EF，在Rt△EFC中，利用勾股定理构造方程，使问题得以解决.

我们知道，一份考卷既是考查区分、学情反馈，同时又要发展师生、引领教学.但是在本次整份试题的命制过程中，一是感觉对矩形知识的考查较弱，二是感觉此题的区分度还不够，于是思考能否把题一中设置的情景置于矩形之中.就是在这样的思考下，得到了试卷中的第19题.

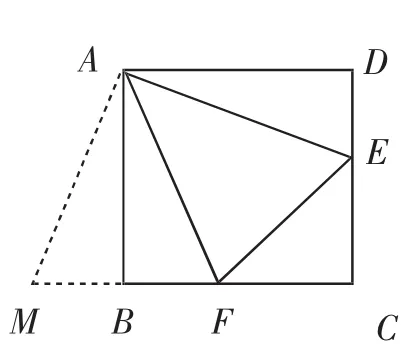
图4

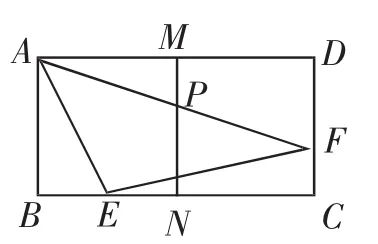
图5

试卷中19题分析：此题的背景是矩形，但可通过分割矩形得到正方形.取AD中点M，作MN⊥BC于N，交AF于点P，从而得到题45°，求AF的长.1的基本图形，易求得MP=，根据中位线定理可求得DF=2MP=，在Rt△AFD中利用勾股定理可求得

三、试题的拓展

对试题进行进一步思考，如果改变题目中的条件，问题能否得解呢？

变式1：如图6，矩形ABCD的边长为AB=3，AD=6，若点E、F分别在BC、DC上，BE=1，且∠EAF=

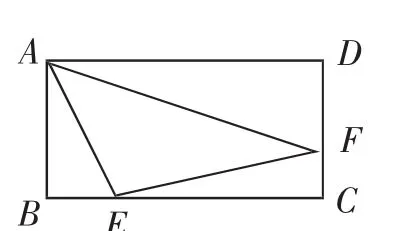
图6

变式2：如图7，矩形ABCD的边长为AB=3，AD=6，若点E、F分别在线段BC、直线DC上，BE=，且∠EAF=45°，求AF的长.

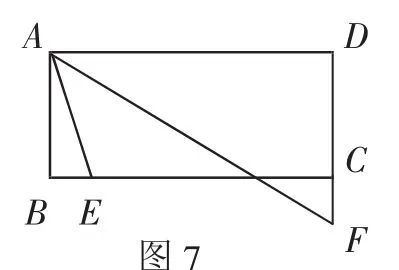
图7

变式3：如图8，矩形ABCD的边长为AB=3，AD=6，若点E、F均在BC上，BE=，且∠EAF=45°，求AF的长.

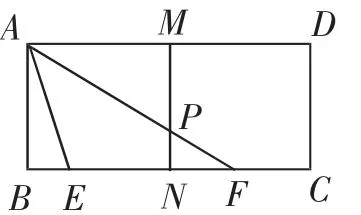
图8

变式4：如图9，矩形ABCD的边长为AB=3，AD=8，若点E、F分别在BC、DC上，BE=2，且∠EAF=45°，求AF的长.

分析1：此题中，边长不是整数倍的关系，但我们可以类比以上问题的解决方法，取AM=3，作MN⊥BC于点N，交AF于点P，可分割得到正方形.然后采用试题中第19题的方法求得MP=，根据平行线分线段成比例定理求得DF=＜DC，说明点F在边DC上，在Rt△AFD中利用勾股定理可求得

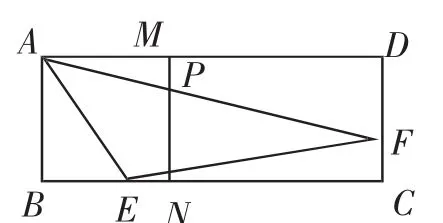
图9

分析2：通过变式4的解答过程，我们可以看到边长为任意数的矩形问题也可以通过转化为正方形的问题来解决，从而使学生真正体验到“千题万题不离母题”的基本活动经验.

四、试题命制过程的思考

1.维护学业水平考试的公平性、客观性

源自教材的问题背景，学生能从教材中找到它的影子，更易于接纳并思考.面对这样的问题，学生的心理活动是积极主动的，因而可以有效激发学生的探究欲望，促进学生的数学思考，鼓励学生的创造性思维.同时源于教材背景的问题，更有利于学生找到解决问题的切入点，提高思维的效率和效度，激发学生数学学习的兴趣，培养学生良好的数学学习习惯，进而掌握有效的数学学习方法.

2.积累解题方法，提高解题能力

问题中的不变量，为试题的“前世、今生和拓展”搭桥.上述问题中，无论它的前世、今生和拓展，都是借助了正方形的特殊性质：四条边都相等、四个角都是直角.正是有了这样的图形背景，为图形的旋转变换创造了必要的条件，为问题的解决提供了思考方向，也为我们命制试题、解答问题提供了方法支持.所以在教学中，我们要引导学生善于从变化中找到不变的特性，用“执果索因”的联想法，体会一题多变、多题同法之数学化归思想的精髓，提高学生发现问题、提出问题、分析问题和解决问题的能力.

3.引领教学，告别题海

源于教材、又高出教材的原创命题，让人会有“回味无穷、渐入佳境”的感觉.面对这样的问题，势必会引领教师重视教材，创造性地利用教材，告别题海，告别对题型的死训练，引导学生走上学习解题、积累方法、感悟思想、开发智慧的“数学育人”之路，进而实现传授知识和技能，关注过程和方法，培养学生良好的学习情感、积极的学习态度和正确的价值观三维目标的高效落实.