固体火箭发动机喷管传热与壁面烧蚀的耦合计算分析①
张小英,向红军
(1.中山大学 中法核工程与技术学院,珠海 519082;2.北京航空航天大学 宇航学院,北京 100083)
0 引言
固体火箭发动机工作过程中排出燃气与Al2O3粒子混合的高温高速喷流,对发动机喷管结构形成强烈的对流和辐射加热,引起发动机喷管的烧蚀破坏,并污染火箭底部的有效载荷,这些现象已经从回收的航天器上得到证实。准确预测高温喷流对发动机喷管的加热,对于火箭底部结构的热防护设计非常重要,低估羽流加热将会导致火箭底部关键设备的烧蚀损坏,估计过高又会使防热设计过于保守而增加死重,并提高发射成本。
针对火箭发动机在高温喷流加热作用下的传热分析,美国宇航局20世纪80年代前开发的火箭发动机推力室传热及温度分析程序均为一维的;1988年NASA开发了三维稳态热分析程序,但不考虑轴向导热和燃气对发动机表面的辐射[1]。Nesbitt J A研究采用一维径向导热和二维径向/周向导热模型,计算一台H2/O2火箭发动机隔热层的瞬态热响应[2]。2002年,NASA Lewis研究中心集成开发了一套火箭发动机导热/对流/辐射耦合分析的三维软件RTE,其中壁面辐射用离散交换系数法(DEF)计算,燃气的吸收和发射用灰气体模型计算[3]。针对火箭工作时热分析的实时性要求,Francisco Alhama采用一维瞬态导热与对流/辐射耦合的模型,用网络法求解喷管壁温随时间的快速变化[4]。近年来,在火箭发动机热分析研究领域还兴起反演研究,Chen Tsung-chien等研究了喷管二维轴对称瞬态传热与壁面热流和温度的实时反演,根据壁面材料内部测点的温度值,反算材料表面的温度和热流分布[5]。
国内学者围绕火箭发动机的温度分析和热防护结构设计,也开展了大量研究。在火箭发动机的热分析和温度计算方面,早期有研究在不考虑辐射换热条件下分析结构的一维传热[6]。后来逐渐发展到研究火箭发动机燃烧室的二维稳态传热,如吕发正建立了火箭发动机推力室传热分析的二维有限差分模型,考虑了壁面间及壁面与燃气的辐射换热[7];董志锐建立了双层壁冷却结构环形燃烧室火焰筒壁面的二维稳态传热/对流/辐射耦合传热模型[8]。后来,针对火箭发动机的三维瞬态热分析成为研究的热点,较早的有韩振兴采用三维有限元模型对液体火箭发动机铣槽推力室的辐射与对流复合换热进行分析[9]。马忠辉建立了多层隔热结构内瞬态导热与辐射的复合换热模型,采用二流法计算结构内部的辐射热流[10];白丹研究了多层隔热结构中瞬时辐射和导热耦合的数学模型,采用有限体积法求解辐射传递方程[11];王保国采用DSMC方法计算了Ballute飞行器壁面的气动热和温度分布[12]。
固体火箭发动机喷管在喷流对流和辐射加热作用下传热烧蚀的计算分析非常复杂。一方面,喷流中的高温燃气是多组分强光谱选择性辐射气体,喷流中燃烧生成的Al2O3粒子有强烈的辐射发射和散射作用,因此喷流对喷管的辐射换热精确计算非常困难;另一方面,火箭发动机喷管多采用金属基体内衬高温下可热解烧蚀的复合材料,喷管喉部及收敛段壁面在喷流加热作用下不断烧蚀变薄,且喷管壁面温度与喷流对喷管的加热热流相互影响。因此,现有研究大都采用均匀灰气体模型计算喷流对喷管壁面的辐射换热,并假定喷管壁温不变条件下计算壁面与喷流的对流和辐射换热,而在计算喷管壁温时假设其厚度不变,这些假设导致计算结果与实际情况存在一定偏差,不能满足先进航天运载技术之火箭发动机精准化热防护设计的需要。为此,本研究将计算火箭发动机高温喷流燃气辐射的波带模型和计算Al2O3粒子辐射的Mie算法,与动边界条件下沿复合喷管厚度方向的一维瞬态导热和热解烧蚀模型相结合,建立喷管壁面导热与内外对流辐射的耦合热分析模型,计算某固体火箭发动机在地面试车工况下复合喷管的瞬态温度与烧蚀厚度,为发动机的精准热防护设计提供详细参考数据。
1 喷管结构/材料与几何参数
本文计算的第一个算例是文献[13]中所采用的试验发动机喷管。试验发动机燃烧室直径为φ144 mm,内置8 mm厚的热防护层。采用复合推进剂,铝粉含量为14%,燃烧温度达3460 K,最大工作时间为23.7 s,燃烧室压强为4.2 MPa,喷管喉径φ11 mm,收敛段和扩张段均为圆锥形,收敛角为56°,扩张角为20°,喷管采用钢制外壳,背衬和内衬采用高硅氧酚醛。文献采用试验方法测量了该发动机喷管的温度场,本文对该发动机喷管内部的流场和壁面温度场进行计算。
本文计算的第二个算例是美国Trident 2 D5弹道导弹发动机,一级发动机燃烧时间64.7 s,工作时间67.4 s,喷管数量1个,喷管喉径350 mm,出口直径1143 mm,出口锥扩张半角22.6°。喉衬材料采用碳/碳复合材料,扩张段材料采用高硅氧-酚醛复合材料。二级发动机燃烧时间73.7 s,喷管数量1个,喷管喉径240 mm,出口直径1372 mm,出口锥扩张半角22.4°。本文计算一级发动机地面试车140 s的喷管传热与烧蚀,为适当简化喉衬和扩张段不同材料的热解分析,假定喷管整体壁面材料均为厚度0.005 4 m的金属基底内衬厚度0.025 m的高硅氧-酚醛复合材料构成,即图1所示的红色金属基底和橙色复合材料内衬。高硅氧-酚醛复合材料的质量组分为高硅氧纤维24%,酚醛纤维20.4%和酚醛树脂55.6%。
2 喷管内流场的计算
对于两个算例的喷管内流场,都采用CEA( Chemical Equilibrium with Applications) 计算复合推进剂化学平衡组分及喷管入口参数,随后利用FLUENT 对固体火箭发动机喷管-尾焰流场进行一体化数值仿真。采用时间推进法及AUSM 空间离散格式数值求解二维轴对称Navier-Stokes 方程组,采用k-ε湍流模型模拟喷流与环境大气的掺混,并考虑了H2、CO、HCl在尾焰流场中的二次燃烧, 采用拉格朗日方法模拟Al2O3颗粒与喷流的相互作用。
3 喷流对喷管的换热计算模型
3.1 喷流对喷管的对流换热计算模型
喷管内壁的对流换热系数用巴兹公式计算[14]:
(1)
式中 粘性系数μ、定压比热容cp、普朗特数Pr均以燃气总温T*为定性温度;Dt为喉部直径;At为喉部截面面积;A为计算截面面积;rc为喷管喉部的曲率半径;σ为定性温度变换系数;pc为燃烧室的压强;C*为燃气的特征速度。
C*计算如下:
(2)
其中,Rg为燃气的气体常数;Pr、μ采用近似计算方法如下:
Pr≈4k/(9k-5)
(3)
式中Mr为相对分子质量。
3.2 喷流对喷管的辐射换热计算模型[15]
喷管内的高温喷流是多种辐射性气体与Al2O3粒子的混合介质,有强烈的辐射发射、吸收和散射特性,吸收/发射/散射性介质中的辐射换热微分方程如下:
(4)
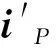
(5)
ΔVPΔω′
(6)
(7)
(8)
高温喷流对喷管壁面的光谱辐射热流qr,λ由喷管壁面近场流体向壁面的投入辐射能量Gλ与壁面的自身辐射强度εEb,λ之差计算,
qr,λ=ε(Eb,λ-Gλ)
(9)
总辐射换热热流qr为光谱辐射热流对全波长的积分。因喷流中的高温燃气是强光谱选择性辐射介质,主要辐射光谱在短波和中波红外波段,故本文将2~6 μm波段等间隔地分为40个波带,分别计算喷流的光谱辐射亮度和喷管壁面的光谱辐射热流,将其他波段合并考虑为无燃气辐射的波带。对喷流中Al2O3粒子因其辐射光谱性不明显,考虑为灰体连续介质。计算喷流对喷管辐射换热所需的燃气光谱特性参数采用HITRAN分子光谱数据库的谱线数据[16],对于单个Al2O3粒子的光谱特性参数采用Mie理论计算[17],粒子云发射和散射系数采用单次独立散射无关性假设计算为单个粒子的作用之和,粒子云的散射相函数计算为8组粒子相函数之数学平均。
4 固体火箭发动机喷管的升温与烧蚀计算模型
喷管内衬高硅氧-酚醛材料对喷管起着热防护作用。随着喷管壁面在高温喷流加热作用下的升温,热防护层的升温和烧蚀将经历5个阶段。第一阶段为热防护层升温,但温度未达到酚醛树脂热解温度300 ℃之前的阶段(Tw<300 ℃);第二阶段为酚醛树脂开始热解至热解完毕,热解层转变成炭化层的阶段(300 ℃ 根据一维平板非稳态导热模型列出热防护层内部节点的传热方程为 (10) 对于内、外边界节点,可根据附加热源法列出传热方程,在热防护层内边界节点,有 (11) 式中qc、qr分别为燃气对热防护层内表面的对流和辐射加热热流(W/m2)。 热防护层外边界与金属基底接触,边界节点的传热方程为 (12) 以上公式中,下标“s”表示热防护层的参数,下标“sm”表示热防护层与金属基底的交界面。 本阶段壁面的传热需考虑喷管复合材料的热解吸热,因此内节点的传热方程为 (13) (14) 在热解层内边界接触高温喷流的节点,传热方程为 (15) 在热解层外边界与金属基底接触面的节点,传热方程为 (16) 以上公式的下标“j”表示热解层的参数,下标“js”表示热防护层与金属基底的交界面。 此阶段炭化层的传热分析方法与热防护层升温阶段相同。 此阶段炭化层材料中的SiO2发生熔融蒸发,不仅导致炭化层的质量损失,SiO2熔融蒸发还会吸收部分喷流对喷管的传热量。SiO2软化熔融层内节点的传热方程写为 (17) 在SiO2软化熔融层内边界接触高温喷流的节点,传热方程为 (18) 对SiO2软化熔融层外边界与炭化层接触面上的节点,传热方程为 (19) (20) 对于SiO2熔融物的汽化与脱落,本文采用熔融层吹扫和碳化层δ准则脱落模型相结合的方法加以判断。当碳化层孔隙率θ≤0.9,采用熔融层吹扫模型,假定熔融层厚度的90%被吹扫至喷管下游壁面,选择90%的吹扫率是考虑到熔融层与未熔基层材料界面处存在一层薄粘性底层作用;当孔隙率θ>0.9时,采用文献[20]提出的δ准则判断烧蚀脱落,即碳化层发生整体脱落。孔隙率计算为 (21) 对于两个算例的喷管内流场,都采用CEA(Chemical Equilibrium with Applications) 计算复合推进剂化学平衡组分及喷管入口参数,随后通过FLUENT 对固体火箭发动机喷管-尾焰流场进行一体化数值仿真。采用时间推进法及AUSM空间离散格式数值求解二维轴对称Navier-Stokes 方程组,采用k-ε湍流模型模拟喷流与环境大气的掺混,并考虑了H2、CO、HCl在尾焰流场中的二次燃烧, 运用拉格朗日方法模拟Al2O3颗粒与喷流的相互作用。 因两个算例计算的喷管内流场参数较接近,这里只给出Trident 2 D5弹道导弹发动机的喷管流场结果,所计算喷管内燃气和Al2O3粒子(文中只给出Dp=3.8、9.6、17.4 μm三组粒子结果)的温度、压力、速度、组分、粒子数密度见图2~图11。 算例1为验证本文的计算模型和方法,计算的文献[13]中试验所用某含铝复合推进剂固体发动机喷管的温度,并与测量的温度结果比较。图12为试车后喷管喉部下游x=4.5 mm截面处,内表面往里4 mm节点处壁面温度Tw的计算值和测量值随时间τ的变化,图13为喷管喉部下游x=4.5 mm处壁温随厚度的变化。图12中,本文所计算该喷管壁面节点温度随喷管试车时间的变化趋势与文献中实验结果一致,但文献测量的壁面节点温度随时间的变化趋势较为平滑,而本文计算的壁面节点温度在τ=7 s和τ=16 s时出现明显阶跃。时间τ=7 s时,材料从初始状态升温到热解温度;时间τ=16 s时,材料热解完毕生成炭化层,不同阶段的传热机理有所不同,因此计算的壁面节点温度出现阶跃。图13中,本文计算喷管喉部下游4.5 mm处壁面温度沿厚度的分布与文献的计算结果接近,但本文计算壁面内侧的温度略低,原因是所采用热防护层材料热解模型不同(文献未给出计算采用的材料热解模型)。 算例2计算美国Trident 2 D5弹道导弹一级发动机地面试车140 s时间的喷管传热与烧蚀。图14为喷管喉部壁面烧蚀厚度随时间的变化,图中随试车时间增加喷管喉部壁面的烧蚀厚度呈阶梯状上升,最大烧蚀厚度为8 mm,平均烧蚀速率为0.057 mm/s。由于热防护材料的热解-炭化-熔融-汽化脱落都从最内层材料逐渐向外层材料发展,每一层新材料均需要经过一定时间才能完全烧蚀,因此壁面的烧蚀厚度随时间呈阶梯状上升。图15为发动机工作后10 s,高温喷流对喷管内壁的辐射与对流热流沿喷管长度的分布,图中喷管收敛段喷流的温度很高,喷流对喷管的辐射热流很强,达到8000 kW/m2,相比之下对流热流则小得多,只有3000 kW/m2。在喷管喉部,喷流加速流动,对流换热急剧上升至与辐射热流相当的数量级;喉部下游喷流的温度和压力都不断下降,因此对喷管的对流和辐射加热热流都大幅下降,辐射热流降幅更快,在喉部下游对流热流大于辐射热流;喷管出口段壁面的对流热流和辐射热流都很小。 图16和图17分别表示发动机地面试车后100 s,沿喷管长度的6个横截面上,壁面内表面和外表面温度随时间的变化。 图18是发动机试车后的7个时刻:τ=20、40、60、80、100、120、140 s,喷管壁面6个厚度处材料层温度沿喷管轴向长度的分布,图中Y表示计算材料层至喷管内表面的距离。 图16中,在喉部前方横截面x=0.077 m和喉部x=0.3 m上,壁面内表面温度在2500~3200 K之间起伏,原因是喉部前喷流对喷管内表面的辐射加热很强,材料不断经历热解-炭化-熔融-脱落,因此温度也发生不断起伏;在喉部下游扩张段前部的横截面x=0.56、0.75、0.95 m上,壁面内表面温度随时间阶段式升高,随着横截面的后移升温台阶的发生时间也相应滞后,在100 s时上述3个横截面的内壁最高温度分别达到2500、2000、1800 K;在扩张段中部横截面x=1.14 m处,内表面温度在试车后的初始阶段0~10 s,初始温度陡升至1600 K后,迅速下降至1100 K,之后直到100 s的时间内,再缓慢地降至1000 K。在喷管的外表面,随着喷管内壁受热升温,喷流加热量逐渐向喷管外壁传递。因此,图17中发动机开始试车后,喷管横截面x=0.077、0.3、0.56、0.75、0.95 m处喷管外表面温度随时间缓慢上升;至外表面温度升至330 K。此时,热防护层内侧温度超过材料的热解温度,材料热解释放出大量能量传递到喷管外表面,导致外表面温度迅速上升;之后,随着喷管内表面温度的稳定,外表面温度也趋于稳定;在喷管横截面x=1.14 m处,因喷流对喷管内壁加热下降,内表面升温幅度小,外表面温度则基本不变化。 在图18中所示的各个时刻,由于喷流对喷管内表面的总加热热流在喉部前沿轴向上升,在喉部后沿轴向下降,因此最内层材料(Y=3 mm)的温度在喉部前沿轴向长度上升,在喉部后沿轴向长度下降;中间层材料(Y=6、9、12、15 mm)的温度受到内层材料的导热和自身蓄热升温进程共同影响,温度沿轴向长度下降,还在扩张段后部(x>1 m)出现材料层温度的跳跃式下降,原因是在喷管下游,喷流中的Al2O3粒子数量急剧下降,对壁面的辐射热流大幅下降,导致喷管壁面温度也陡然下降;外层材料(Y=18 mm)的温度在20 s时还没有发生明显变化,在其后的几个时刻外层材料升温,并呈现沿轴向长度前高后低的特征。在τ=60 s及以后各时刻,内层材料温度曲线上的不连续处是烧蚀节点。 由图18可见,最内层材料(Y=3 mm)在τ=60、80 s时,喷管入口部位和喉部的节点被烧蚀,在τ=100 s及以后时刻,喷管收敛段及喉部的最内层材料都烧蚀了;在τ=140 s时,喷管收敛段除最内层材料烧蚀,中间层材料(Y=6 mm)也出现局部烧蚀。 图19选取发动机试车后的3个时刻(τ=40、80、140 s),给出喷管壁面的温度分布云图,其中可清楚地看到沿壁面厚度喷管温度的急剧下降,在贴近喷管内表面的高亮区域温度很高,在贴近喷管外表面的区域温度较低。 比较τ=80、140 s的壁面温度云图,后者的高温区域和烧蚀区域都更厚。 为研究固体火箭发动机复合喷管的辐射对流换热与壁面烧蚀,对喷管与管内高温喷流辐射与对流换热、以及与外部环境换热作用下的壁面升温与材料烧蚀,分为基体材料升温-热解-热解层碳化-SiO2熔融-碳化层脱落五个阶段,建立一维非稳态模型并编制了热分析程序,对某模型火箭发动机喷管试验工况和Trident 2 D5弹道导弹发动机地面试车工况进行计算分析。研究表明: (1)所计算模型火箭发动机喷管传热与烧蚀计算结果与文献的实验结果有较好一致性; (2)所计算Trident 2 D5弹道导弹一级发动机地面试车时,喷流对喷管收敛段壁面的辐射热流很强,达到8000 kW/m2,而对流热流只有3000 kW/m2,喷管喉部的对流热流与辐射热流数值相当,约为9000 kW/m2,喷管出口段壁面的对流热流和辐射热流都很小; (3)在τ=100 s及以后的时刻,喷管收敛段及喉部的最内层材料都有明显烧蚀,烧蚀厚度随试车时间呈阶梯状上升,140 s时,喉部烧蚀厚度最大为8 mm,平均烧蚀速率为0.057 mm/s; (4)随着喷管内表面受喷流加热不断经历热解-炭化-熔融-吹扫脱落,内表面温度随着时间在2500~3200 K范围内起伏变化,壁面中间节点和外表面温度随时间连续上升; (5)喷管壁面各厚度材料层温度随轴向长度增加而下降,且在扩张段后部(x>1 m)出现材料层温度的跳跃式下降,只在喷管喉部之前,内表面温度随轴向长度增加而上升。4.1 热防护层升温阶段(Tw<300 ℃)
4.2 热防护层热解阶段(300 ℃
4.3 热解层开始炭化但炭化层未达到剥蚀厚度阶段(800 ℃
4.4 SiO2软化熔融阶段(1750 ℃
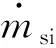
4.5 SiO2熔融物的汽化与脱落阶段(3000 ℃
5 计算结果与分析
5.1 流场计算结果
5.2 喷管传热计算模型与方法的验证
5.3 Trident 2 D5一级发动机地面试车的喷管传热与烧蚀
6 结论

