基于抛物线的一条性质的类比推广

张留杰

(北京市陈经纶中学 100020)

众所周知，椭圆、双曲线、抛物线均是由一个平面截圆锥所得的平面图形，所以这三种曲线具有许多共同的几何性质．在教学和研究中，我们应该善于从一种圆锥曲线的特殊性质入手，试图将这种性质类比推广到另外两种曲线上，进而探究该性质背后蕴含的圆锥曲线的一般特征，揭示问题的本质．下面以一道高考试题为例，谈谈探究历程．

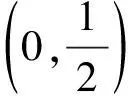
(Ⅰ)求抛物线C的方程，并求其焦点坐标和准线方程；

(Ⅱ)求证：A为线段BM的中点．

1 试题的解答与反思

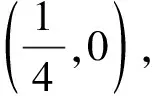
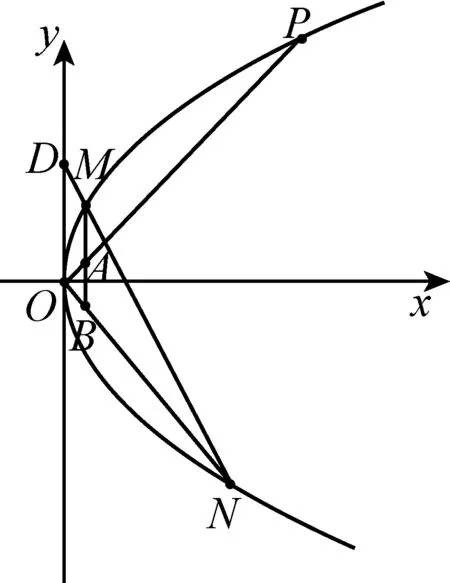
图1

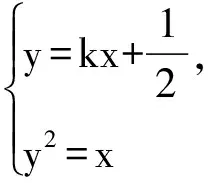
2ky2-2y+1=0，

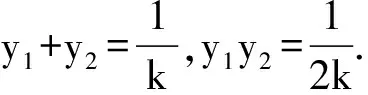
又直线OP的方程为y=x，MA⊥x轴且交OP于点A，所以A(x1,x1)；

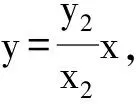
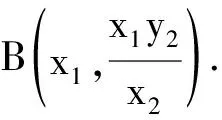
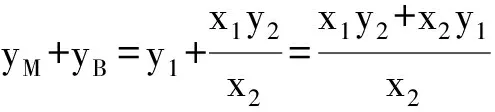
所以点A是线段BM的中点．

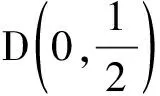
2 试题的纵向、横向推广

经过探究，若点D是y轴上的动点，可将试题做如下推广．

结论1如图2，过y轴上一点D(0,y0)作抛物线C：y2=2px的切线DP，切点为P，过点D引直线l与抛物线交于不同两点M、N，过点M作x轴的垂线分别与直线OP、ON交于点A、B，则点A是线段BM的中点．

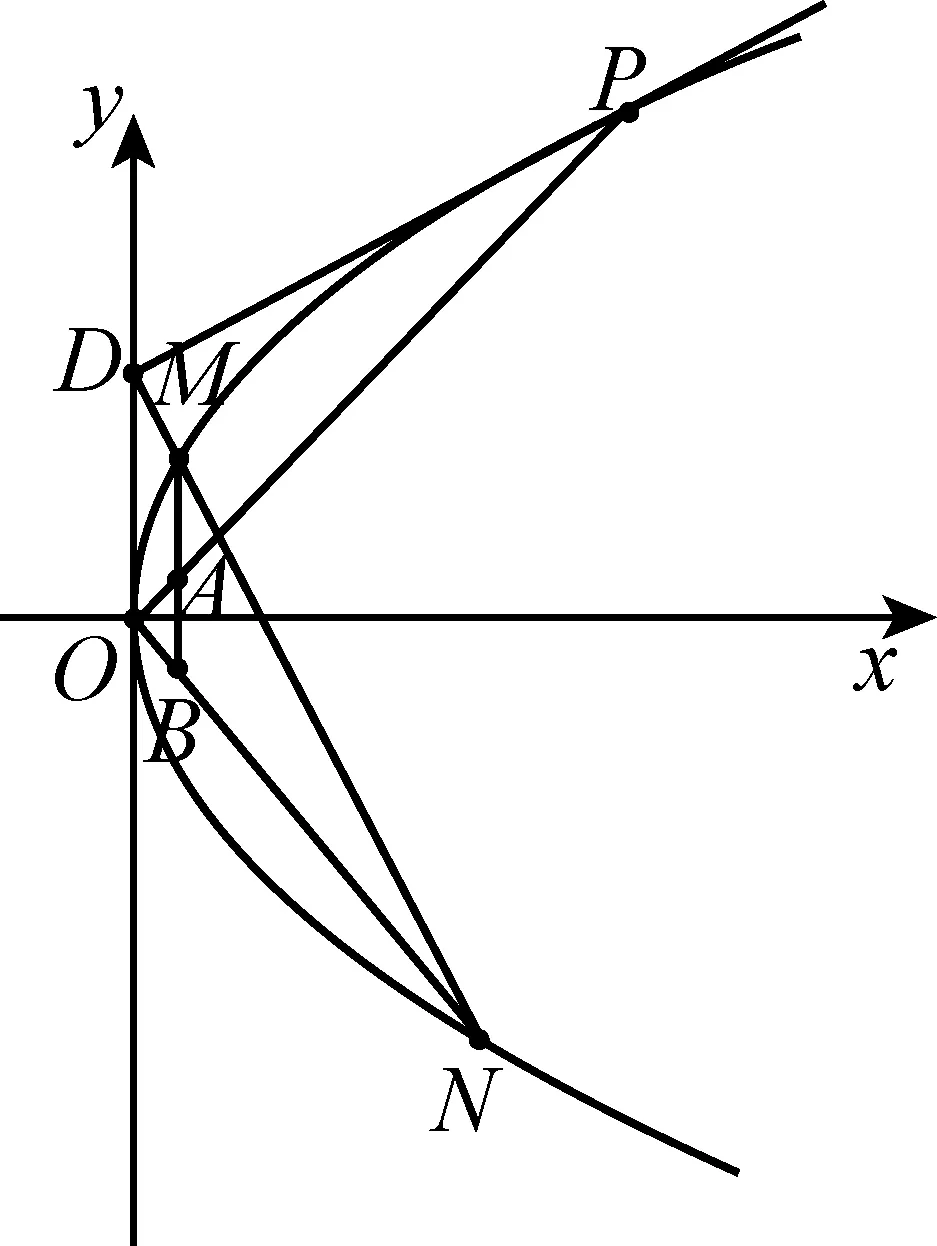
图2

证明设切线DP：y=hx+y0，P(xP,yP)，

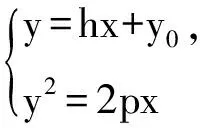
①

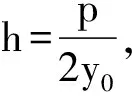
解得y=2y0，即yP=2y0，

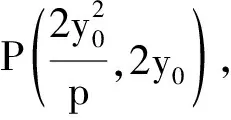
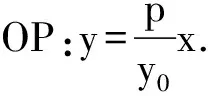
设直线l：y=kx+y0，M(x1,y1)，N(x2,y2)，

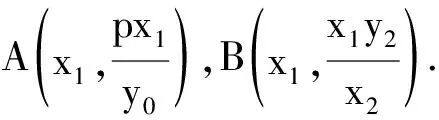
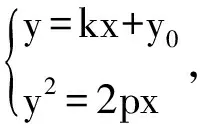
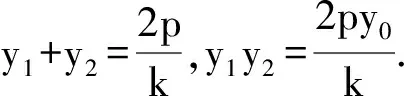
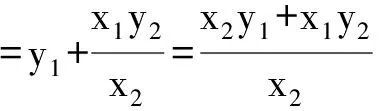
所以点A是线段BM的中点．命题得证．

能否将此结论类比到有心圆锥曲线呢？如果将原点O看作抛物线的顶点，则可以类比到椭圆、双曲线过顶点的切线，于是得出如下结论(以椭圆为例)：

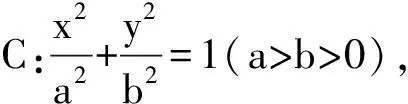
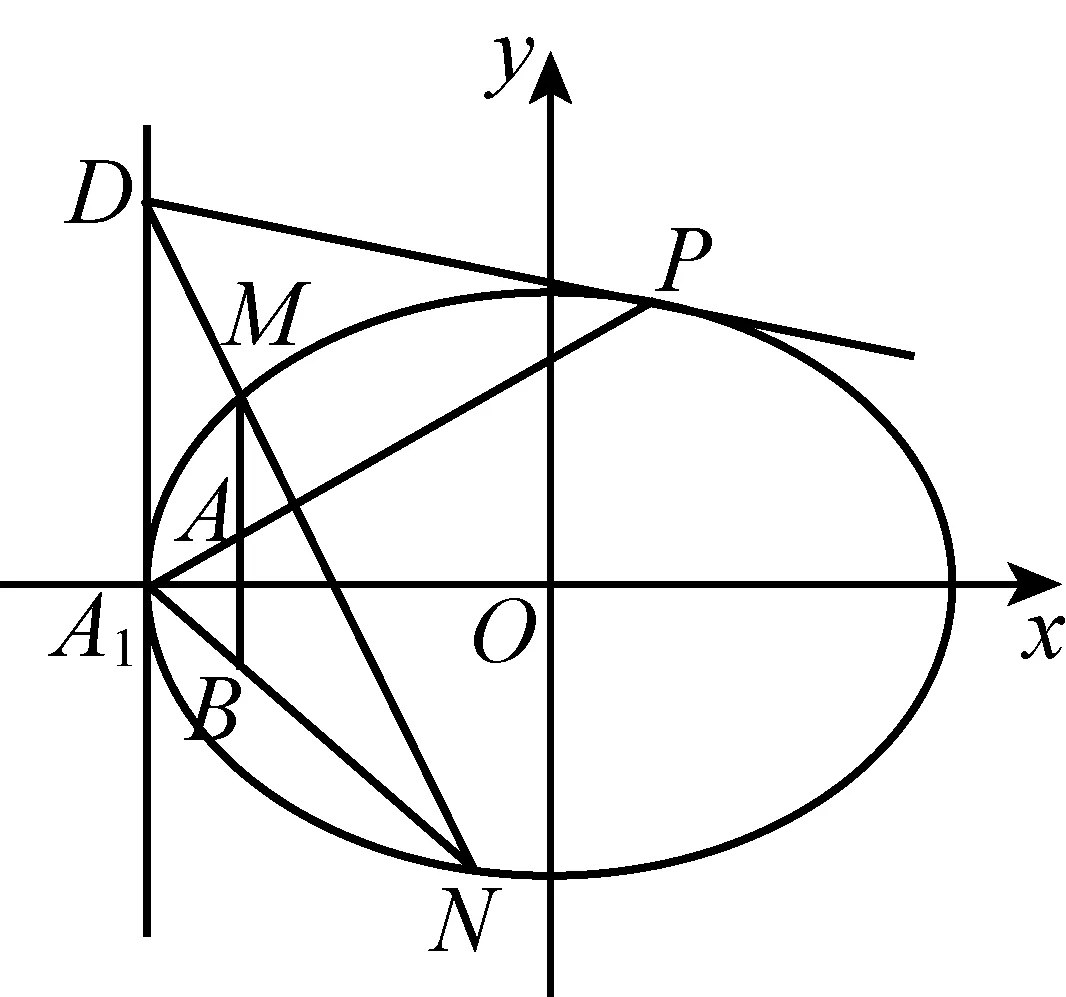
图3

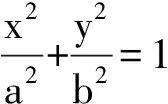
设直线l：y-y0=k(x+a)，

M(x1,y1)，N(x2,y2)，

所以将x=x1分别代入方程①、②可得

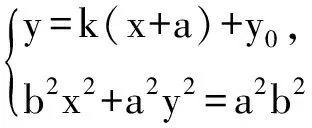
要证点A是线段BM的中点，

根据它们的坐标只需证yB+yM=2yA，

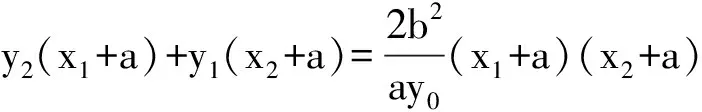
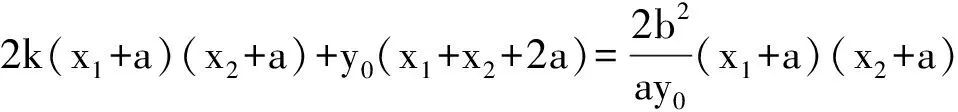
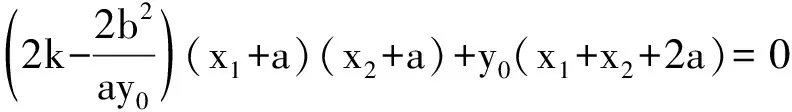
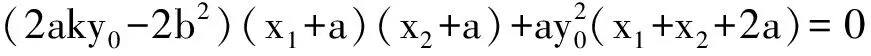
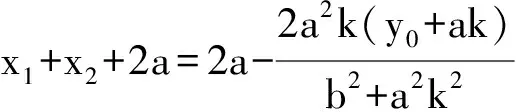
(x1+a)(x2+a)=x1x2+a(x1+x2)+a2

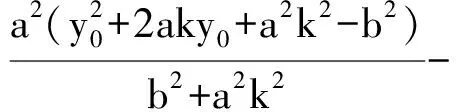
所以代入③式，只需证明

⟸2aky0+2a2k2-2aky0-2a2k2=0.

显然成立．故点A是线段BM的中点．

类似地，对于双曲线，该结论也成立．

3 试题蕴含的一般规律

上述结论中的点D能否弱化为圆锥曲线外任一点呢？过点M的垂线又如何随切线的变化而变化呢？经过一番鏖战，得出更具有一般性的结论如下：

结论3点D是圆锥曲线W外一点，过点D引曲线W的两条切线DP、DQ，切点分别为P、Q．过点D引曲线W的割线l交曲线于两个不同点M、N，过点M作切线DQ的平行线分别与直线QP、QN交于点A、B．则点A是线段BM的中点．

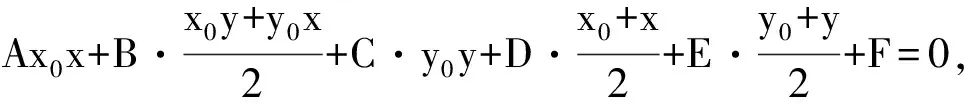
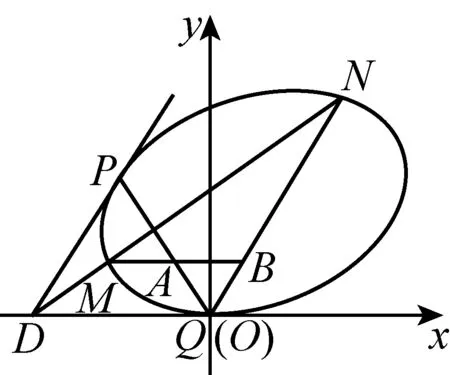
图4

证明(以椭圆为例)如图4，以点Q为坐标原点，切线DQ所在直线为x轴，建立如图所示的平面直角坐标系．设曲线W的方程为ax2+bxy+cy2+dx+ey=0，D(t,0)(t≠0)，根据极点与极线的关系，可得切点弦QP的直线方程为：(2at+d)x+(bt+e)y+dt=0，

因为PQ过原点，则d=0，

所以QP的方程化为2atx+(bt+e)y=0．

设直线l：x=hy+t，M(x1,y1)，N(x2,y2)，

由直线MA平行于DQ可得

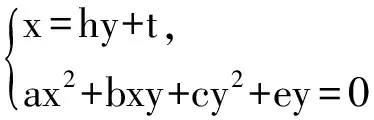
(ah2+bh+c)y2+(2aht+bt+e)y+at2=0，

依题意，要证点A是BM的中点，

只需证明xM+xB=2xA，即证

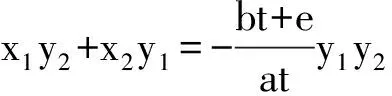
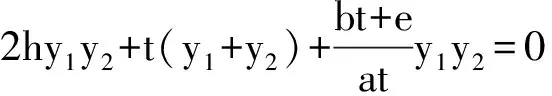
⟸(2aht+bt+e)y1y2+at2(y1+y2)=0

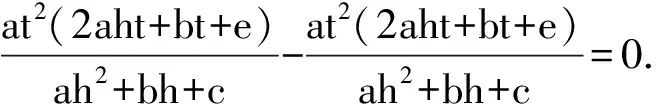
故点A是线段BM的中点．命题得证．

经过层层探究，得出更一般的结论，凸显了这道高考试题丰富的内涵，彰显了类比猜想的魅力，正如牛顿所说“没有大胆的猜想，就做不出伟大的发现”，以此与大家共勉．