针对一型深水结构物的水下声场计算与试验研究

孙建刚，赵晓宇，吴有生，邱立凡

（中国船舶科学研究中心，江苏 无锡 214082）

0 引 言

工作于深海环境的深水结构物需要承受极高的静水压力，如果选用单圆柱壳的结构形式，根据相关的强度设计理论，设计潜深与耐压壳直径成反比，与壳板厚度成正比，一味的加大板厚往往会超出板材供货规格和加工建造能力，因此为了保证设计的有效舱容，将多个较小直径加肋圆柱壳相组合的结构形式就成为较合适的方案，这也将成为深水结构物耐压设计的一个发展方向。

针对有限长圆柱壳的声辐射问题，国内外的学者多年来进行了深入的研究，Laulagnet等[1-2]研究了敷设柔性阻尼材料的有限长圆柱壳的声辐射性能；商德江等[3]利用有限元加边界元方法对双层加肋圆柱壳在端部球头处轴向激励下的振动和声辐射作了数值计算，系统地比较了内外层圆柱壳的法向振动响应和场点声压的规律；陈美霞等[4]基于Donnel壳体理论，将横向构件的作用看成壳体上的反力和反力矩，推导了带无限长刚性障板的双层柱壳的近场声压解析解，并与消声水池中的试验结果作了比对；姚熊亮等[5]基于弗留盖壳体理论和Helmholtz波动方程来求解流固耦合方程，得出了有限长双层圆柱壳在径向点激励下的振动响应和声功率，讨论了托板结构和舷间介质对声辐射的贡献；祁立波等[6]基于三维水弹性方法分析并比较了单/双层加肋圆柱壳纵向以及垂向激励下的声辐射特性；邹明松等[7-11]发展了适用于任意形状的、具有复杂内外结构的弹性浮体流固耦合振动与水中声辐射分析的三维声弹性理论方法，利用该理论方法计算了球壳、加筋圆柱壳以及实尺度船体等结构的水下声辐射，与解析结果、试验结果吻合较好。

本文针对一型多耐压壳体双层深水结构物，基于三维声弹性方法，对其场点声压传递函数进行了数值计算，经与混响修正后的模型声学测试数据相比对，二者吻合程度良好。文中最后对该型深水结构物场点声压的周向分布特征进行了计算研究。

1 数值建模与干模态分析

深水结构物的水平剖面如图1所示，三个环肋增强的耐压圆柱壳沿正横方向“一”字形排列，柱壳间通过横向板架结构及耐压通道连接，在耐压结构的外部敷设非耐压的蒙皮结构，蒙皮与柱壳间通过六根桁材连接，蒙皮结构采用十字交叉的扶强材加强，结构物的上下两端为加强的耐压封板，结构的主体尺寸参数为：R1/t1=112.5、R1/l1=4.5、R1/L=0.225、R2/t2=90.714、R2/l2=3.175、R2/L=0.159、R3/t3=16.667、R3/L=0.063、t4/L=0.001、t5/L=0.001、t6/L=0.001、t7/L=0.006、A1/（l1h1）=0.413、A2/（l2h2）=0.386 和 A3/（l3h3）=0.254，其中 R1，t1，l1分别为中间柱壳的半径、厚度和肋距，R2，t2，l2分别为两侧柱壳的半径、厚度和肋距，R3，t3分别为柱壳间耐压通道的半径、厚度，L为模型垂向尺寸，t4，t5，t6，t7分别为蒙皮、纵桁材、实肋板和耐压封板的厚度，A1，A2，A3分别为中间柱壳环肋、两侧柱壳环肋和蒙皮两向加强筋的截面积，l3为蒙皮加强筋的间距。结构材料均为钢材，其密度ρs=7 800 kg/m3，杨氏模量E=2.1e11Pa，泊松比ν=0.3，结构损耗因子取0.02。

图1 模型水平剖面视图Fig.1 Horizontal section of model

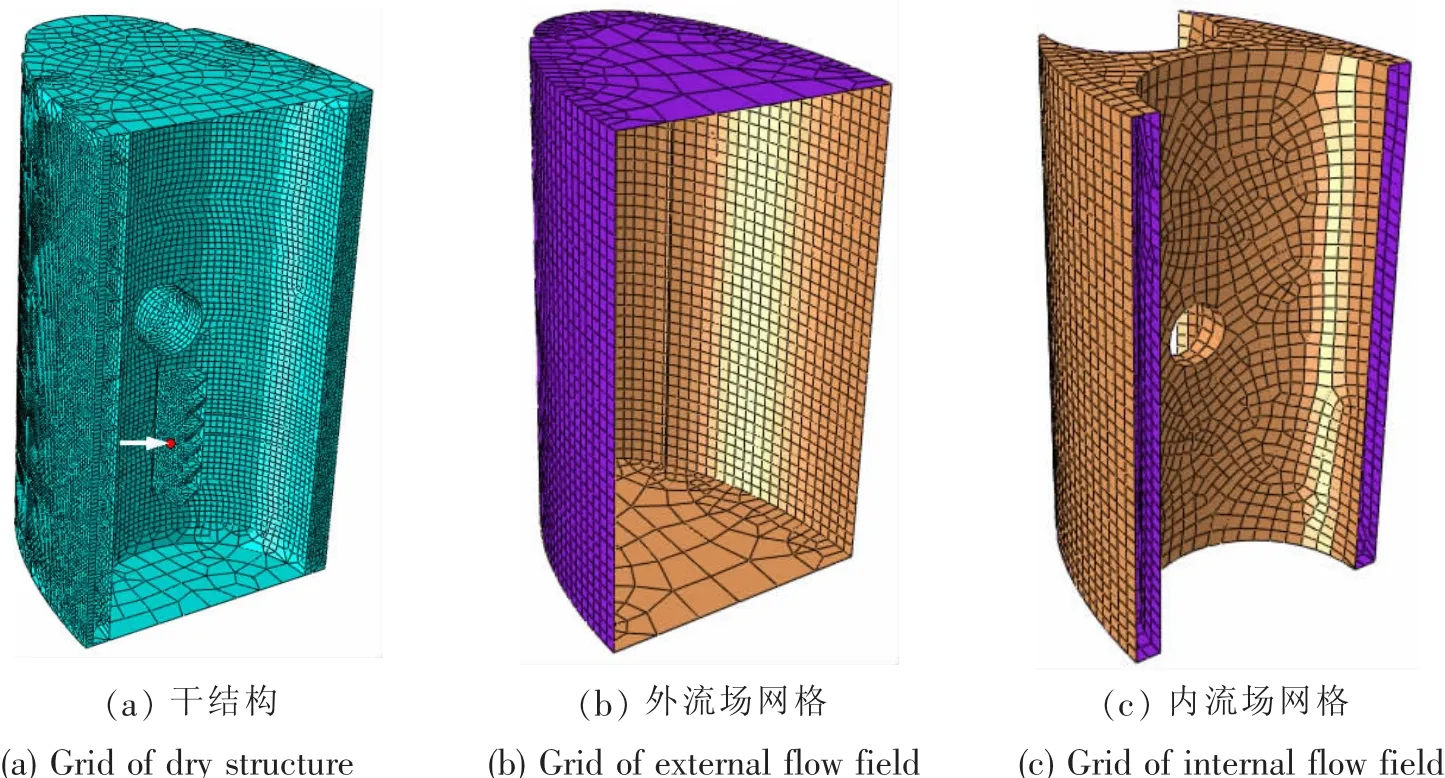
图2 数值模型Fig.2 Numerical model

建立数值模型如图2所示：干结构模型节点总数113 048，单元总数120 384（与声介质接触的干结构单元数74 640），分别针对舷间声介质和外部声介质建立湿面元网格，网格总数4 921（外流场网格单元数2 020，内流场网格单元数2 901）。在中间柱壳单侧的设备基座上施加法向简谐单位力激励（激励位置位于基座面板的板格中心，在图2（a）中由箭头标出）。

数值模型为自由边界条件，在0.1～1 925 Hz频段内对其进行干模态分析，得到7 950阶弹性模态，部分低阶模态的振型如图3所示（为便于观察，对每一阶干模态将外层蒙皮振型和内层柱壳振型单独显示）。

图3 干模态振型Fig.3 Modal shape in vacuum

2 三维声弹性理论

本文针对深水结构物水下场点声压的求解是基于三维声弹性理论方法[8]，由展开定理，微幅振动的水下结构相对于平衡位置的运动和变形可表示为：

结构表面上的流固耦合界面条件为：

主坐标位移响应满足的广义线性水弹性力学运动方程为：

式中：［a］，［b］，［c］分别为干结构的广义质量、广义阻尼和广义刚度阵；［A ］，［B］，［C］分别为广义流体附加质量、广义流体附加阻尼和广义流体恢复力系数矩阵；｛q｝为广义主坐标列向量；｛Ξ ｝为广义力向量。广义流体附加质量、广义流体附加阻尼和广义流体恢复力系数矩阵计算公式如下：

与水池试验环境相对应，采用有限水深的Green函数：

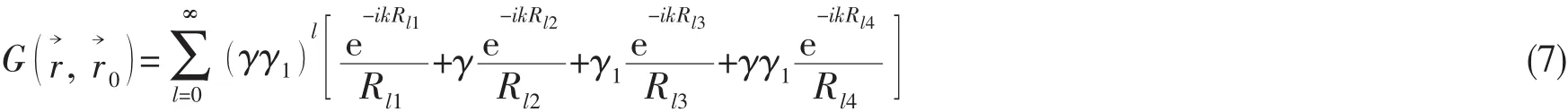
式中：γ 和 γ1分别为水底和水面的声反射系数， 分别取为，水深取为h=13 m，潜深取为h1=5 m。

与各阶模态辐射波速度势相对应的简单源边界积分方程为：

则对应于第r阶干模态的振型速度为：

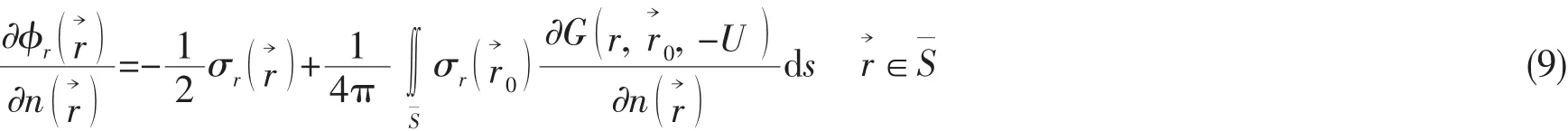
由（9）式和（2）式即可求解各阶模态的湿表面源强σr，代入（8）式后，可导出结构振动所诱导的辐射速度势：

场点声压由船体振动引起的辐射速度势得出：

场点声压级定义为：

式中：p0=1×10-6Pa·Hz-1/2为声压的基准值。

3 模型试验

在露天水池中对深水结构物模型进行了水下噪声测试，模型布放于水池中心位置，布放区域最大水深约13m，模型几何中心的布放深度为水下5 m，绕模型轴线设置两周共48个计算场点，按周向15°均布，两周场点距模型轴线径向距离分别为6 m和15 m，水听器布放深度为水下5 m，场点分布如图4（a）、（b）所示。对模型结构采用MB modal-110电磁激振机激励（最大激振力500 N，激励信号可调频段2～6 500 Hz），配套功放为MB 500VI，激振机通过橡胶隔振器柔性安装在中间柱壳单侧的设备基座上（激励位置与图2数值模型一致），激振机安装频率约13.2 Hz，安装布置情况如图4（c）所示。水声测量采用B&K 8104水听器。测量与分析系统采用B&K的PULSE 3560D多通道采集分析仪。

各水听器布放位置场点声压信号的信噪比结果如图5所示，由图可知在100 Hz以后的频段信噪比满足测试要求。

图4 试验布置图Fig.4 Testing arrangement

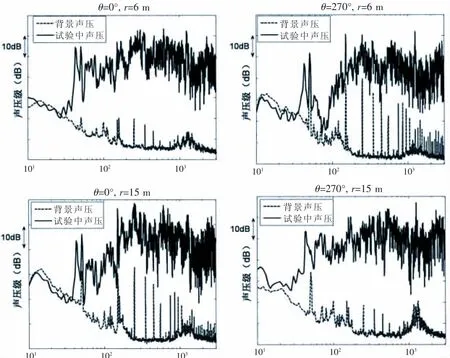
图5 场点声压信号信噪比Fig.5 Signal-to-noise ratio of sound field pressure

试验水池中的声场较为复杂，不存在严格意义上的扩散声场，但在工程应用中，可以通过扩散声场的处理方法对测得的近场声压数据进行混响修正。由统计声学的理论，在混响场中的实测场点声压级为：

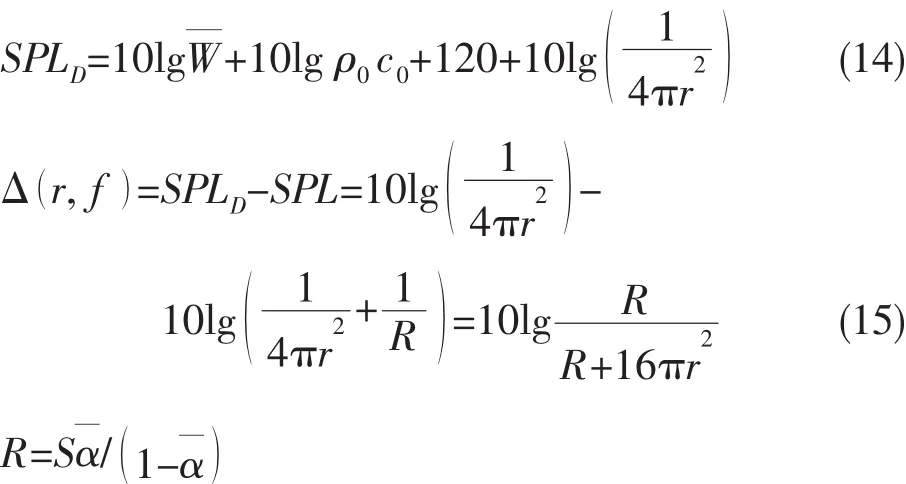
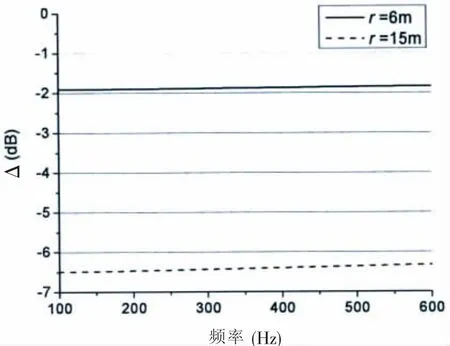
图6 混响修正曲线Fig.6 Reverberation correction curves

4 场点声压传递函数计算结果的试验比对

将场点声压实测结果进行混响修正并对激励力进行归一化处理，将归一化结果与计算结果进行比对，如图7、图8所示。由图可知，除个别场点的结果外，二者在100～600 Hz的低中频段内量级水平和趋势一致，吻合得较好。图8中（θ=315°，r=6）场点的比对结果较不理想，经初步分析可能与试验水池在该指向上局部区域的复杂声场环境有关。

分别对内外周各24个场点声压传递函数进行能量平均，得出其在100～600 Hz频段的平均声压传递函数如图9所示，分析其总声级，计算值均比实测值偏低0.8 dB左右。

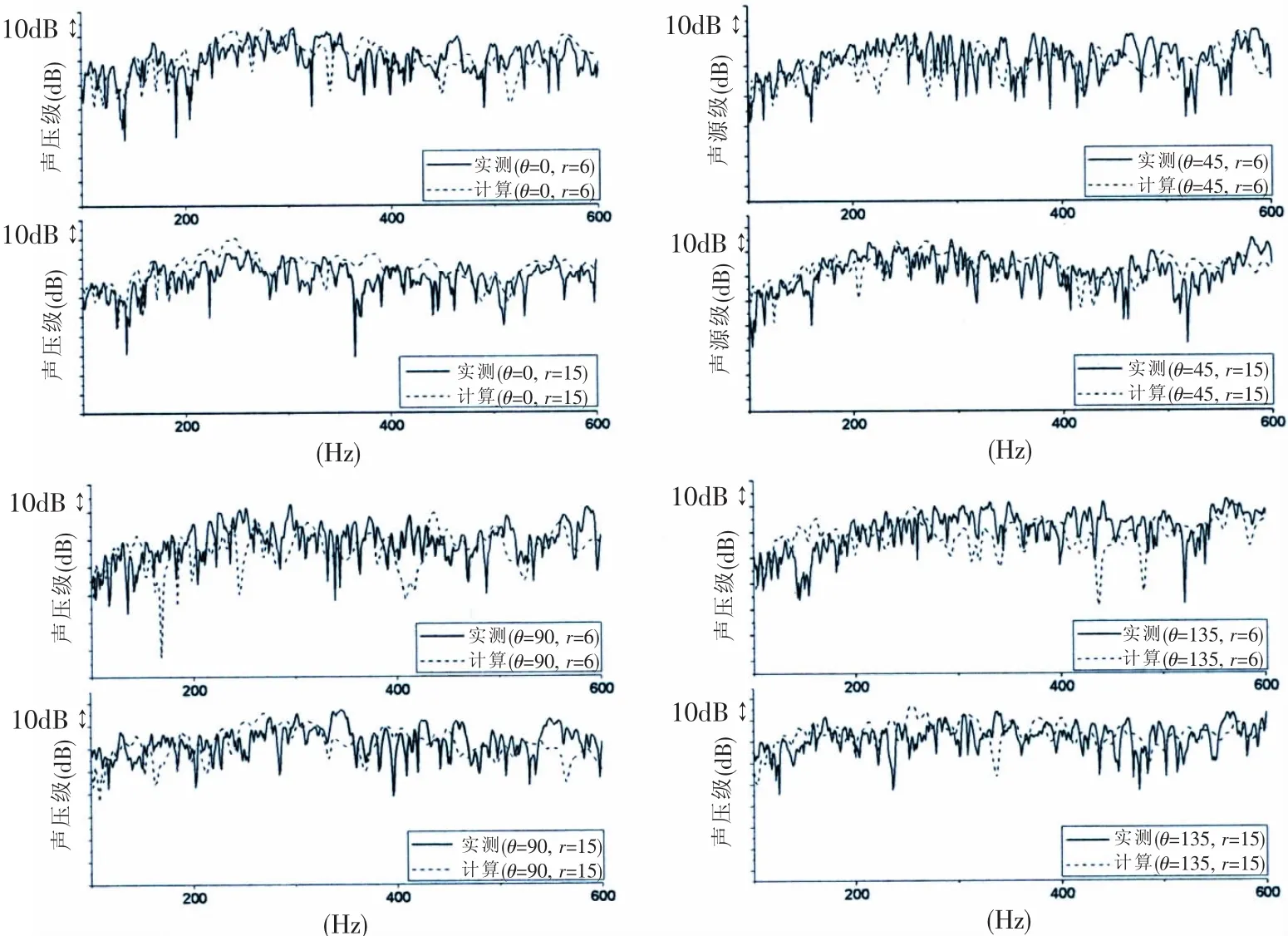
图 7 场点声压传递函数（θ=0°，45°，90°，135°）Fig.7 Transfer function of field pressure(θ=0°，45°，90°，135°)

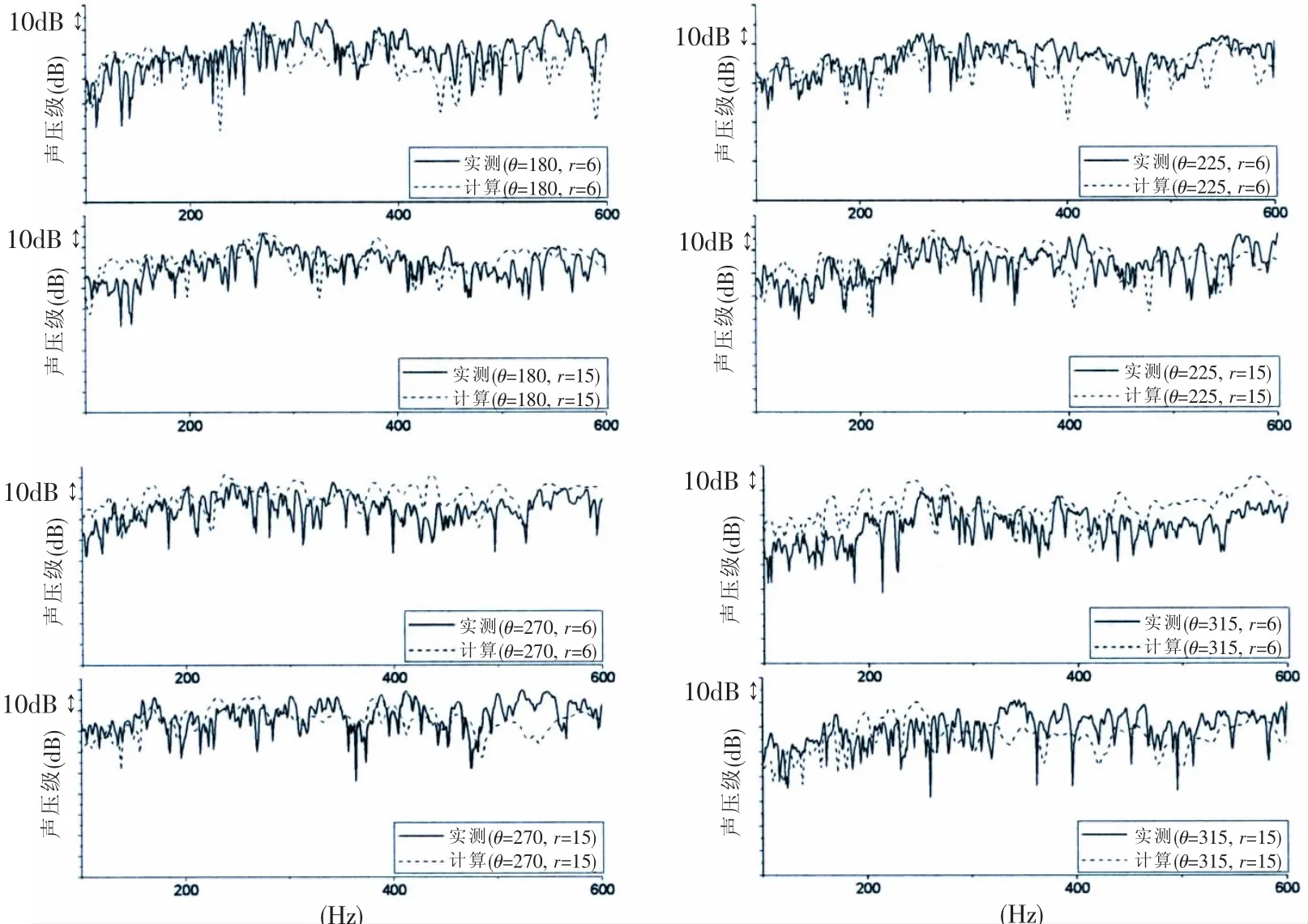
图 8 场点声压传递函数（θ=180°，225°，270°，315°）Fig.8 Transfer function of field pressure(θ=180°，225°，270°，315°)

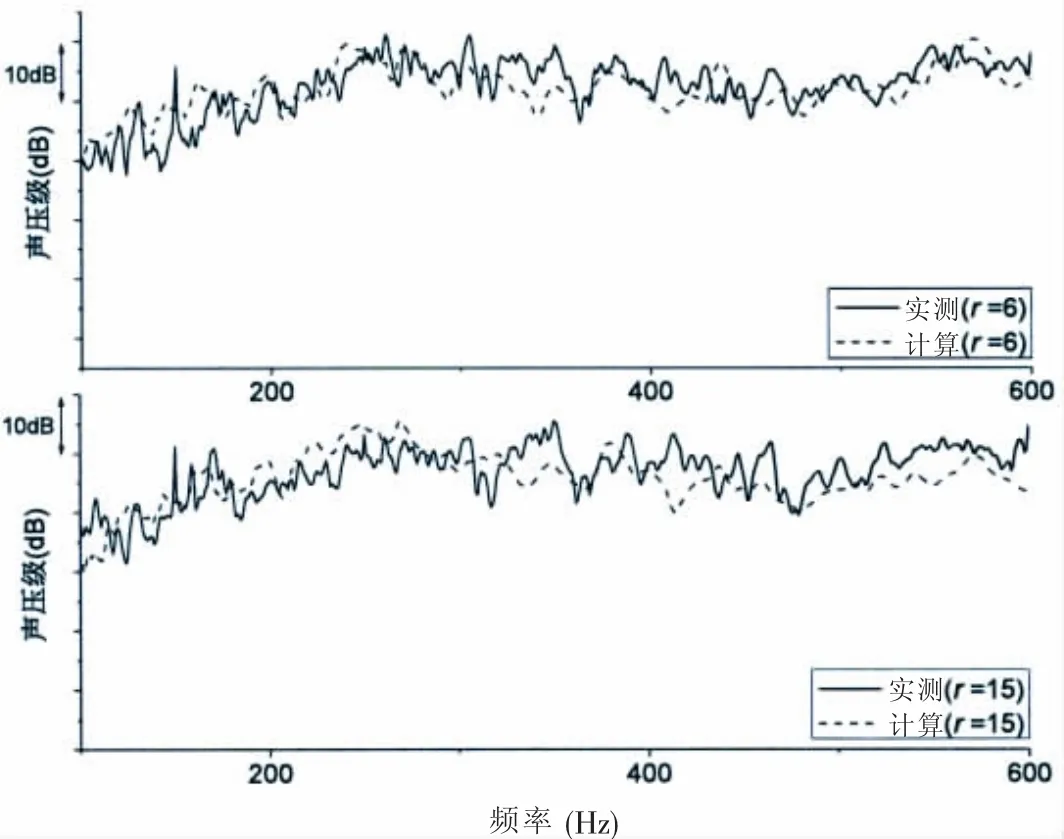
图9 场点声压传递函数（周向平均）Fig.9 Circumferentially averaged transfer function of field pressure

5 场点声压周向分布特性

由15 m远处场点声压传递函数的计算结果求得100/200/300/400/500/600 Hz共六个频率点处的场点声压周向分布图，如图10所示。由图可知，在不对称载荷的激励下，模型的场点声压呈现左右不对称的特性，随着分析频率的提高，波瓣数目呈逐渐增多趋势。此外，单从上述六个频率点处的场点声压周向分布来看，声场并没有显现出明显的指向性特征。

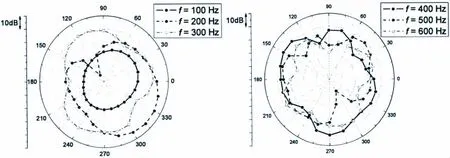
图10 场点声压周向分布Fig.10 Circumferential distribution of field pressure

进一步在100～600 Hz频段内对各点的场点声压进行能量求和，得出场点声压总级（带级）的周向分布，如图11所示，图中总声压级最大值位于周向θ=330°处，最小值位于周向θ=105°处，二者相差约4.5 dB。结合受激励基座所处空间方位，可知场点总声压级最大值的周向方位位于壳体受激励位置的外法向附近。

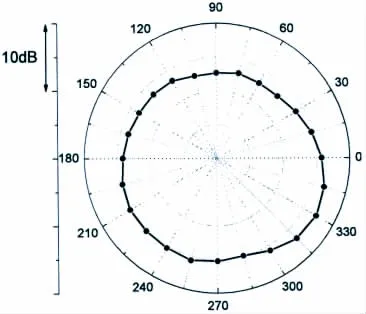
图11 场点总声压级周向分布Fig.11 Circumferential distribution of overall sound pressure level

6 结 论

本文针对一型深水结构物，基于三维声弹性方法进行场点声压的数值仿真计算，并在露天水池进行了模型的声学试验验证，得出以下一些结论：

（1）基于统计声学的方法得出所用水池的混响声对场点声压实测值的贡献，在距模型轴线6 m和15 m处分别为1.9～1.8 dB（100～600 Hz）和 6.5～6.3 dB（100～600 Hz），表明相对于试验模型为有限尺寸的试验水池中进行的声学测试，混响声的干扰不可忽略，需要进行混响修正；

（2）在100～600 Hz的频段将场点声压传递函数的数值计算结果与混响修正后的测试结果进行比对，二者量级水平和大致趋势普遍吻合良好，将各个周向点的场点声压传递函数进行能量平均，计算值和实测值的误差小于1 dB，说明三维声弹性方法对于多耐压壳体复杂结构物的声学问题的求解具有较高的精确度；

（3）计算表明，深水结构物存在着与加肋圆柱壳相一致的以下声场分布规律：随着分析频率的提高，声压分布图的波瓣数目逐渐增多；场点声压总级最大值的周向方位接近壳体受激励位置的外法向方向。