典型含水复合结构在聚能装药水下爆炸作用下的毁伤

王长利，周 刚，马 坤，陈春林，戴湘辉，冯 娜，李虎伟

（西北核技术研究所，西安 710024）

0 引 言

伴随聚能型水中兵器的发展，为提高战斗部的作战效能以及水中兵器的生存能力，国外对于聚能侵彻体在水介质中的运动以及聚能装药的设计开展了相关研究。Lampert[1]通过使用气炮发射圆柱形弹丸侵彻水的方式研究了水对于高速侵彻体的影响，得到了不同水层厚度对圆柱形弹丸的速度衰减以及弹丸的墩粗变形规律。Janzon[2]通过实验和数值计算研究了EFP在水中运动的情况，对比了铜和钽两种药型罩的效果，给出了优化的聚能战斗部模型参数。Blanche[3]对比了EFP及聚能杆式弹丸对含水目标的侵彻效果，给出了不同方案的设计方法。从文献调研情况可以看出，国外对聚能侵彻体的理论研究以及实验研究均起步较早，实验手段完善，但近年来，再无公开报道。

国内对该问题的研究主要集中在实验与数值计算方面。叶本治、李成兵[4-5]等分析了聚能战斗部爆炸以及高速弹丸在水介质中的相似特性。他们认为水下高速弹丸（射流）运动规律及破甲能力，满足几何相似和弗鲁德相似准则，弹丸对复合靶板的侵彻深度遵循相似律准则。杨莉、叶本治、裴明敬、王团盟[6-9]等研究指出，聚能侵彻体在水中运行速度呈指数衰减，运动过程会产生空化，同时，后效的毁伤与侵彻体的速度和质量密切相关。这些研究成果为应用于水中的聚能装药设计提供了有力的支持，为开展模拟实验研究提供了依据。但以上研究大多基于数值计算和地面模拟实验，并未在水中进行过全面的研究，与实际使用情况不同。

聚能装药水下爆炸产生的主要载荷是聚能侵彻体和水下爆炸冲击波，其对含水复合结构的毁伤主要为聚能侵彻体对钢+水+钢的贯穿以及水下爆炸冲击波的联合毁伤。本文通过水下爆炸实验和数值模拟，对典型含水复合结构在聚能装药水下爆炸作用下的毁伤进行了研究。该工作可为水中聚能装药技术研究以及水中结构抗冲击设计提供参考。

1 实验设计

本文针对两种典型含水复合结构（下称复合结构）在聚能装药水下爆炸作用下的毁伤进行研究。复合结构如图1所示，包括前板、后板、水舱以及后效靶组成，前板和后板之间为一定厚度的水层，后效靶放置在密封箱体中，周围介质为空气不同的含水复合结构的水层与靶板厚度不同。

聚能装药如图2所示，其直径为108 mm，高度为109 mm，采用高能装药，装药为3 kg TNT当量，药型罩为变壁厚设计，直径85 mm，质量260 g，材料为紫铜。聚能装药采用波形控制器实现多点起爆，确保成型稳定。

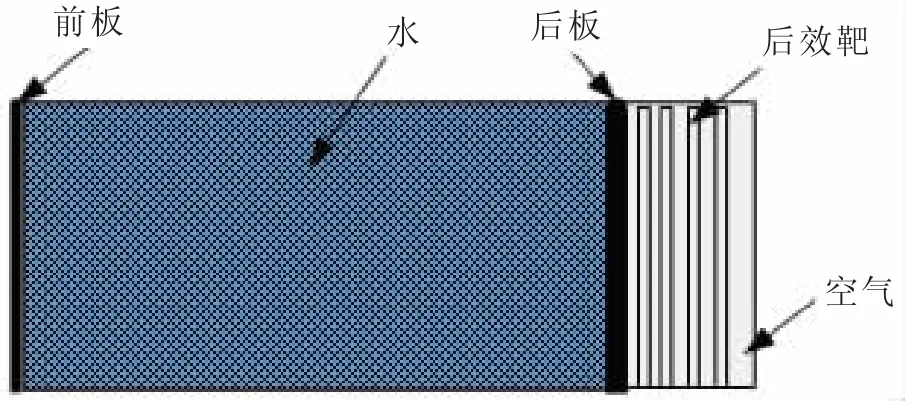
图1 复合结构示意图Fig.1 Water partitioned structure diagrammatic sketch

图2 聚能装药及波形控制器Fig.2 Shaped charge and shock wave controller

图3 典型含水复合结构Fig.3 Water partitioned structure

典型含水复合结构如图3所示，具体参数见表1。实验弹安装在薄壳密封筒体内，距离水舱前板121 mm。两种典型结构的前板（1#靶）为3 mm厚Q235钢，后板（2#靶）分别为13.5 mm厚45#钢和10 mm厚921A钢板，水层厚度分别为667 mm和250 mm。密封箱体中放置有5层6 mm后效靶，材料为Q235钢，后效靶之间间隔10 mm，用于考核聚能侵彻体的贯穿水舱后板后的侵彻能力。

表1 含水复合结构参数Tab.1 The parameters of water partitioned structure

实验系统组成及测点布局如图4所示，在距离爆心为0.5 m、1 m和3 m位置上安装压力传感器，测量水中自由场冲击波压力；在复合结构中的侵彻通道上布置铜箔探针，测量聚能侵彻体在水介质中的运行速度；在前板及后板上距离聚能装药中心线0.1 m处分别布置PVDF薄膜压力传感器，测量靶板表面的反射压力。实验水池直径11 m，深度10 m，实验中，典型结构放置于水面以下3.5 m位置。

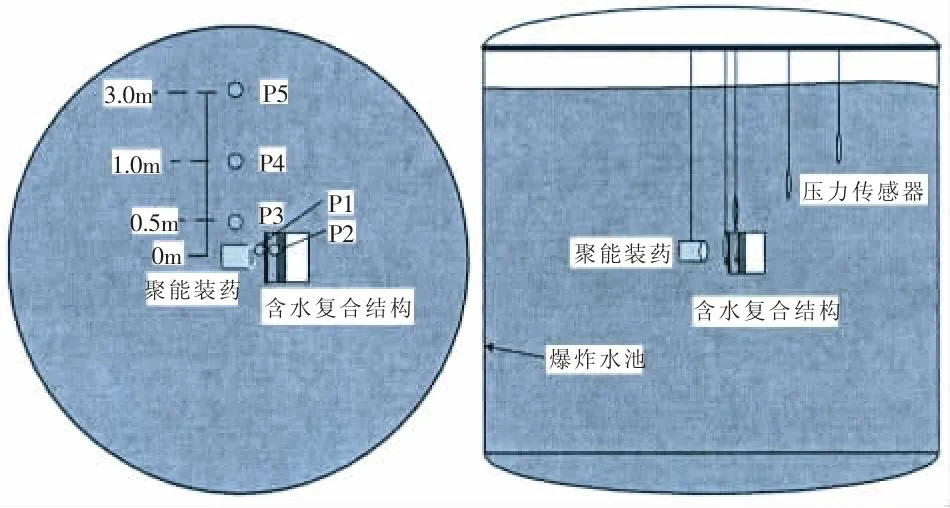
图4 实验系统组成及布置Fig.4 Sketch of the experimental setup

图5 No.1结构破坏情况Fig.5 Damage of water partitioned structure in test 1

2 实验结果

第一发实验中，靶板的破坏情况如图5所示，水舱前板呈花瓣型撕裂孔，背面外翻，卷边处有弹坑和铜迹，孔径水平230 mm，垂直220 mm。后板发生脆裂，靶板内陷，中心有圆孔，四周有四条主裂口，拼合碎裂后，可以还原穿孔形态，中心部位贯穿孔径约47 mm。密封箱体内的3#～5#后效靶被穿透，穿透厚度共计18 mm，7#靶背板上有轻微隆起，箱体六面发生内凹。

第二发实验，靶板破坏情况如图6所示，水舱前板严重撕裂，背部外翻，孔径约300 mm，卷边有一处明显铜残留，破孔上侧破坏严重，下侧有较轻铝壳压痕；后板破孔略偏上，形状为椭圆，水平尺寸31 mm，垂直尺寸43 mm，靶板内陷，侵彻体穿透后板后，又穿透了整个密封箱体，穿透后效靶厚度总计为36 mm。最后一块靶板上的穿孔为近似三角形的不规则孔，整个箱体六面内陷。

侵彻体穿越水层后的速度是决定其侵彻能力的主要因素，因此在水舱后板前安装有铜箔测速探针，根据侵彻体通过两层导通的铜箔的时间可以得到侵彻体的速度。实验结果统计如表2所示。

图6 No.2靶板破坏情况Fig.6 Damage of water partitioned structure in test 2

表2 实验结果Tab.2 Results of the experiments

3 结果分析

3.1 结构破坏分析

从实验结果上看，两种典型复合结构水舱后板和后效靶都产生了较为严重的穿孔，孔径约为聚能装药直径的1/3，箱体受压力作用而产生塑性变形，向内侧凹陷。对于667 mm水层结构，侵彻体在后板上穿孔之后，穿透后效钢板厚度为18 mm；而对于250 mm水层结构，侵彻体穿透复合结构后板以后，可再穿透6块总计36 mm Q235间隔靶，并有一定余速。从侵彻体穿越水层后的余速看，实验2的侵彻体速度为2 440 m/s，实验1的侵彻体速度为2 018 m/s，水层对侵彻体的速度衰减起到了较为明显的作用。

实验中，水舱前板出现了约Φ230 mm的孔洞，同时伴有明显的撕裂痕迹，分析认为，水舱前板不仅遭受了侵彻体的破坏，而且还受到炸药爆轰产物的作用。由于前板较薄（3 mm），其抗冲击和抗拉伸能力较弱，因此，其穿孔破坏形式可以归类为瓣裂穿孔，并且随后遭受炸药爆轰产物的作用，前板被严重撕裂，从而形成直径远远大于侵彻体直径的侵彻孔洞。

两发实验的水舱后板厚度不同，从结果可以看出，后板上均呈现了Φ30～40 mm孔洞，并且孔洞前后均有明显的材料熔化、飞溅的痕迹，显示了高速撞击下材料的类流体性质。921A靶板中心为规则的圆形孔洞，而45#钢靶板在受到侵彻时伴随着沿侵彻孔向四周方向的碎裂，开裂情况严重，中心孔附近有大块碎片崩落，经过收集拼接能够还原侵彻孔。由于45#钢材料的韧性较差，在高速侵彻过程中容易发生断裂，而921A具有较高强度的且同时保持较好的韧性，故在侵彻过程中仅在中央形成孔洞。

3.2 冲击波压力

冲击波垂直作用于刚性壁时，发生正反射。反射压力可按空气中爆炸方法进行计算。

入射冲击波波阵面参数与反射波阵面的压力与密度的关系式为[10]：

式中：p1、 ρ1为入射波阵面的参数；p0、 ρ0为未扰动水的参数；p2、 ρ2为反射冲击波阵面参数。

冲击波压力与密度关系：

水的等熵方程：

式中：n=7.15～8.0—常数；A=299～386 MPa—常数。

根据水中冲击波选取不同的压力与密度关系式以及水的等熵方程，将方程（1）、（2）、（3）式联立，因 p1、p0、 ρ1、 ρ0已知，故可以求出 p2、 ρ2。

根据水下爆炸相似理论公式[11]：式中：Pm为压力峰值，MPa；对于 TNT，k=53.3，α=1.13；W 为炸药的 TNT 当量，kg；R 为爆心距离，m。

根据实验测点布置，测点偏离侵彻轴线100 mm，对于667 mm水层结构，P1距离爆心200 mm，P2距离爆心850 mm，对于250 mm水层结构，P1距离爆心200 mm，P2距离爆心的430 mm。实验后的结构壁面反射冲击波压力峰值及自由场压力测量与计算结果如表3所示。

表3 自由场及壁面反射冲击波峰值Tab.3 Peak free field pressure and reflected blast wave pressure

P1、P2为冲击波在刚性壁表面的反射，P3～P5为水中自由场压力峰值。从表中可以看出，壁面反射的压力以及自由场压力与理论估算均相差不大，由于装药为薄壳，而药型罩仅对正向的压力分布有影响，因此，装药形式（是否为聚能型）对其侧向自由场压力的影响可以忽略。两发实验中，水舱前板壁面压力均超过了1 GPa，这已经远超过了实验用钢板（Q235钢）的破坏强度，因此这也是水舱前板产生严重的撕裂的主要原因。冲击波透过水舱前板和水层，传递到复合结构后板表面，并发生反射，此时，冲击波经过水层的衰减，下降至200～450 MPa，已不足以使复合结构后板产生撕裂。

以667 mm复合结构为例，分析压力波形变化。图7为结构壁面反射压力波形，从图中可以看出，冲击波过后，水舱前板上的PVDF（P1）由于靶板的撕裂而遭到破坏，很快就失效了，但其压力上升部分清晰有效。水舱后板上的压力有多次振动，这是由于冲击波阵面在界面上多次反射以及应力波在钢板中传播，致使水舱后板附近点的冲击波压力不规则振动造成的。图8为装药侧向自由场的压力结果，由图可以看出，其与非聚能装药的结果（经验公式）相近，衰减趋势也基本相同。由于该装药的外壳为2 mm铝壳，其对装药侧向爆炸的能量影响不大。

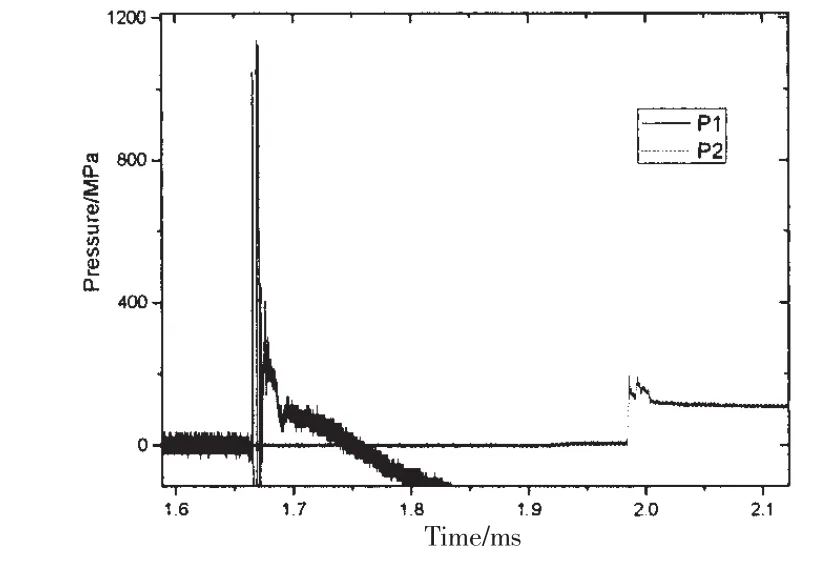
图7 No.1靶板表面压力波形Fig.7 Surface pressure of the target in test 1

图8 No.1自由场压力波形Fig.8 Free filed pressure in test 1

3.3 水舱后板表面冲量分析

（1）自由场冲量

在水下爆炸过程中，设炸药在无限水介质中爆炸，忽略重力影响，基于量纲关系，基尔克乌特—别泽理论给出的自由场冲量的近似公式为[12]

式中：I为单位面积上的自由场冲量，kPa·s；W为炸药装药量，kg；R为爆心距，m；对TNT而言，C=5.75，γ=0.89。

（2）结构表面冲量

将水舱后板看作四周固支方板，水下爆炸冲击波与板的相互作用，是造成结构毁伤的主要原因之一。假定材料为理想刚塑性，水介质为不可压缩理想流体，水介质与板以相同的速度运动，不考虑板端部的影响，忽略空气阻力的影响，有[13]

将牛顿第二定律应用于平板运动，可以得到结构表面获得的冲量

式中：θ为衰减时间常数；pm为峰值压力；；Ic为结构壁面获得的冲量。

将相关参数代入公式（5）、（8）中，可以得到两种复合结构的后板表面冲量，具体如表4所示。从结果可以看出，同一结构中，结构表面冲量Ic远小于自由场冲量I，这是由于板的运动造成的，从计算公式上可以看出。随着水层厚度的减少，结构表面的冲量也有较大增加，这个冲量是造成水舱后板产生大塑性变形（内凹）的主要原因。根据实验后测量后板结构的中心位移情况来看，由于结构表面冲量Ic计算过程中考虑了板的运动，与实验情况更为接近。

表4 水舱后板表面冲量计算结果Tab.4 Results of the impulse on backboard by computation

3.4 水舱后板及后效靶的破坏过程

以667 mm水层结构为例，按照实验模型对多层间隔后效靶的侵彻破坏过程进行数值计算分析，结果如图9所示。爆炸后聚能装药产生长径比约为3：1，头部速度约3 000 m/s的高速侵彻体后，贯穿水舱前板，进入水层。高速侵彻体在穿越水层过程中，由于空化作用，形成空腔，侵彻体在空腔中运行[14]。侵彻体头部由于受到水介质的冲击作用，发生质量堆积与墩粗，同时伴随有质量侵蚀，侵彻体长度因此逐渐缩短。

图9 侵彻体对靶板的侵彻过程Fig.9 Penetration of penetrator on the targets

在t=600 μs时，侵彻体穿透了667 mm厚的水介质层，开始对多层后效钢靶进行侵彻。侵彻体质量被严重侵蚀，此时侵彻体质量只占侵彻初期的20%～30%，速度也只有初速的60%左右。对多层后效靶的侵彻效果就取决于残余侵彻体的质量和速度。

在t=630 μs时，侵彻体贯穿水舱后板，水舱后板穿孔直径约29 mm。与此同时，水舱后板整体由于压力的作用，向内发生凹陷。在经历大约300 μs后，侵彻体一共贯穿了3层共计约18 mm的后效靶，其剩余质量和速度都已经无法再对靶板造成侵彻破坏。数值计算得到的靶板穿孔与凹陷情况与实验基本相同，证明数值计算的可靠性。

3.5 侵彻体在水介质中的速度及质量变化规律

根据数值计算结果，侵彻体头部速度与侵彻体运行距离的关系如图10所示，设复合结构前板所在位置为0 mm。从图中可以看出，可将侵彻体速度按照头部所处位置分为三段：入水前、水中以及出水后。入水之前，侵彻体在成型过程中，速度逐渐增加，最高到约3 400 m/s，当头部撞击前板后，头部速度发生下降。进入水中后，弹体速度呈指数形式逐渐衰减。头部出水后，在“出水点”与水舱后板以及后效靶作用，速度急剧下降，直至停止。

根据文献[7]，侵彻体的速度变化可以用以下公式描述：

图10 侵彻体在水中的速度变化规律Fig.10 Decay of penetrating velocities in water

式中：A、B、C为实验拟合曲线系数；u0为入水初速度，ux为侵彻体在水中位置x处的速度。根据实验和计算的结果，本文研究的侵彻体在水介质中的运动速度为：

由于侵彻体与钢板的作用以及水层对弹体的侵蚀，侵彻体的质量也在不断的发生变化，以667 mm水层为例，侵彻体质量随距离的变化如图11所示。药型罩与残余侵彻体的对比如图12所示，药型罩质量为260 g，在侵彻体成型过程中，药型罩有一定的质量损失，约80%的质量形成侵彻体，当其与前板作用后，剩余质量约为药型罩质量的40%，此时，侵彻体进入水中，由于头部和水接触作用，质量呈指数形式衰减，慢慢趋于缓慢。试验后，对回收到的侵彻体进行称重，剩余质量约50 g，占药型罩质量的20%，残余侵彻体略呈椭圆型，直径约30 mm，小于实验中靶板的穿孔。

侵彻体速度以及质量的变化导致侵彻体动能的变化，侵彻体穿越水层后的残余动能决定了其对后板以及后效靶的侵彻能力。

图11 侵彻体质量比随水中距离的变化Fig.11 Decay of penetrator mass in water

图12 药型罩与回收残余弹体Fig.12 Liner and residual projectile

3.6 不同水层厚度对结构的侵彻的影响

保持前板及后板的厚度不变，对不同水层厚度的弹体侵彻情况进行了分析。后板的破坏情况如表5所示。可以看出，随着水层厚度的增加，出水后，侵彻体穿透的总钢板厚度逐渐减少，当水层厚度为1 000 mm时，后板不能造成穿孔。后板的中心永久位移随水层厚度的增加，逐渐减少，这是因为随着水层厚度的增加，后板所受到的冲击波冲量逐渐减少，因此，其中心永久位移有逐渐减少的趋势。图13为不同水层厚度对应的后板以及后效靶的毁伤情况。

表5 不同水层厚度情况下水舱后板的破坏情况Tab.5 Damage of the combined targets under different condition

图13 不同水层厚度时后板及后效靶的破坏对比Fig.13 Damage of the backboard and the effective pates in the box

3.7 侵彻路径上的结构壁面压力

由于水舱后板侵彻路径上的压力变化难于测量，其又是结构穿孔毁伤的主要因素，通过计算，对水舱后板压力变化进行了数值计算分析。计算模型上的测点分布如图14所示，模型以弹道中心线为轴，在中心向外20 mm处侧依次取点，P1～P10为选取的测点，将各个测点的压力变化情况统计如表6。

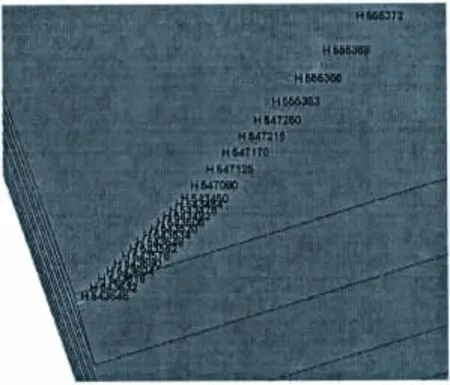
图14 侵彻路径复合结构后板测点分布Fig.14 Test points on the backboard along the penetration path

表6 水舱后板表面测点压力Tab.6 Backboard surface pressure of the tank

图15 侵彻路径上后板测点压力变化Fig.15 Pressure on backboard along the penetration path

图15为测点压力随时间变化波形图。从波形图上可以看出，由于高速侵彻体冲击水介质，因此在侵彻体头部产生激波。弹前激波早于聚能侵彻体到达钢板，在图中的前部有较为明显的压力信号（图中放大部分），其在侵彻体之前作用于壳体，使其产生形变，由于幅值不大，不能够对结构造成毁伤。在侵彻体到达之前，压力波有多次的振荡，侵彻体到达后，结构表面的冲击压力陡然升高，最高至4 000 MPa，此时的压力信号为激波压力和该点相邻水舱后板上单元压力共同作用的结果。在侵彻体的冲击作用下，靶板受到了更严苛的应力环境，这是造成水舱后板穿孔毁伤的主要原因。弹轴中心直径40 mm处的压力峰值降到了730 MPa，小于材料的破坏压力，与穿孔直径30 mm基本吻合。

4 结 论

本文通过实验和数值模拟，对典型含水复合结构在聚能装药水下爆炸作用下的毁伤进行了研究。从结构的毁伤模式、靶板壁面反射压力及自由场压力的变化、结构表面冲量计算、后效靶的破坏过程、侵彻体的速度及质量衰减、水层对后板及后效靶破坏的影响以及侵彻路径上的压力变化等方面，对毁伤进行了全面分析，可以得到如下结论：

（1）聚能装药作用下，水舱前板发生较大孔洞的严重撕裂，水舱后板产生穿孔，孔径约为聚能装药直径的1/3。在本实验条件下，聚能侵彻体穿透水舱后板后，仍能侵彻多层后效靶。

（2）聚能装药侧向的自由场冲击波压力与爆炸当量相关，受药型罩影响不明显，在偏离侵彻路径一定距离上的壁面反射压力与理论计算结果相当。

（3）侵彻体在水介质中运动过程，其头部速度呈指数衰减，侵彻体质量衰减率随距离的增加而减少，残余侵彻体的质量占药型罩质量的20%左右；侵彻体的剩余动能是决定毁伤能力的重要因素。

（4）随着水层厚度的增加，侵彻体对后效靶的侵彻深度以及水舱后板的中心永久位移逐渐降低，对结构的毁伤程度降低，对水层1 000 mm结构，后板仅产生塑性变形。

（5）侵彻路径上的壁面压力变化表明，弹前激波先于侵彻体作用于结构表面，结构穿孔破坏是冲击波与侵彻体共同作用的结果。