基于小波能量谱分析与SVM的柴油机气阀间隙异常故障诊断
蒋佳炜,胡以怀,柯 赟,陈彦臻
(上海海事大学,上海 201306)
0 引言
在旋转机械故障的研究中,由于旋转机械的振动信号在频域内的能量分布具有比较明显的特点,所以基于振动信号的故障诊断一直是学者们的研究热点。基于统计分析和时域分析并利用机器学习的方法在机械故障诊断方面极具潜力,但是这些方法在柴油机故障诊断中运用却不是很多[1-2]。一方面,柴油机振动信号是瞬时的,如果没有合适的降噪方法与适当的特征提取手段,就无法运用机器学习来进行模式识别;另一方面,柴油机的振动信号与许多运动机构有关,一个振动信号由多个激振力产生。作为柴油机机构中重要的运动部件,阀门、活塞环组和配气机构是柴油机振动信号噪声的主要来源,根据其振动信号的小波能量谱分析,可以从能量分布的角度对机械振动信号的特征进行有效提取[3],从而实现对这些运动部件的振动诊断。
随着计算机技术的发展与智能算法的进步,支持向量机(Support Vector Machines,SVM)与神经网络算法在机械故障诊断中的应用也取得了巨大的成功[4-6]。设计1套预测及智能检测专家系统,该系统能对未来时间范围内发生的故障做出预测,但是知识的获取及将领域知识转化为规则却比较困难,且一旦建立专家系统,它不能处理知识库规则以外的新情况,会影响预测的准确度和精度。SVM被认为是一种有效的机器学习方法,相比其他传统的方法,其拥有更好的泛化性能[7]。
针对柴油机振动信号的特点,本文试图利用小波能量谱分析对柴油机的振动信号进行特征提取,将能量在不同频段上的分布作为特征向量输入SVM,训练SVM模型使之针对不同的振动信号与故障模型进行有效的分类,从而获得精确的故障分析结果。
1 故障模拟试验
本次试验使用的是4135高速柴油机,本文使用的数据全部采集自实体柴油机试验。4135高速柴油机型号为 4135AC、机号为 A0422497,其具体参数如表1所示。
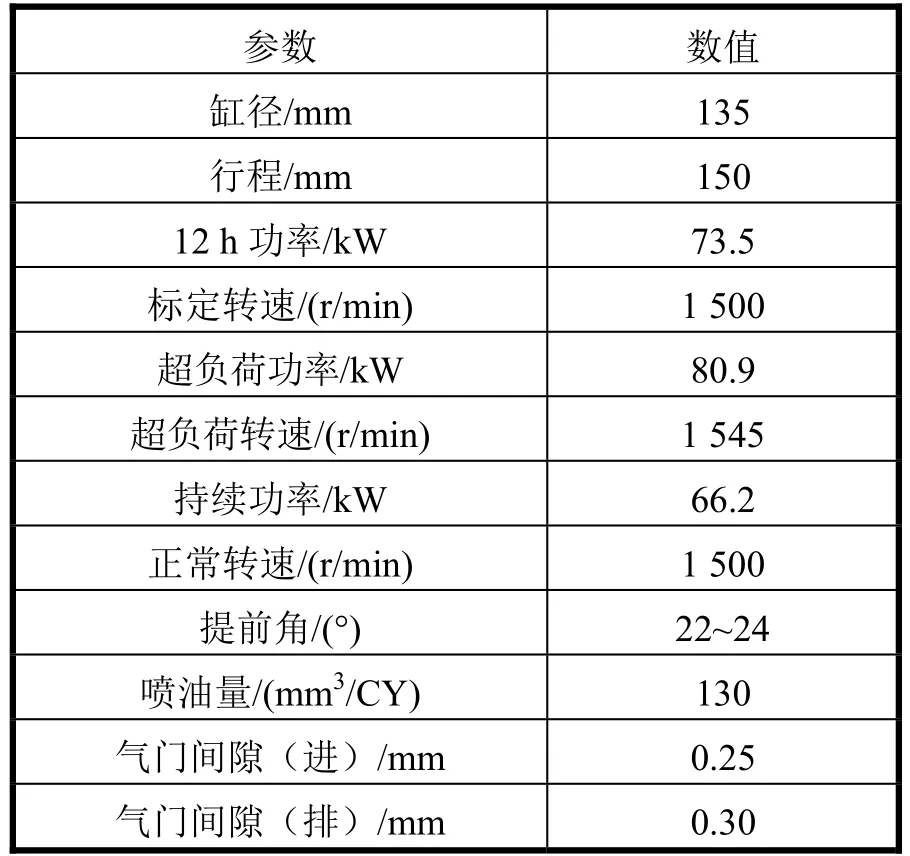
表1 高速柴油机参数表
对 4135柴油机第一缸振动信号进行分析,试验数据总共分为4组,分别为700 r/min工况下,气阀间隙正常和异常产生的数据,以及900 r/min工况下,气阀间隙正常和异常产生的数据。正常情况下的进气阀间隙和排气阀间隙分别设置为0.25 mm和0.30 mm;异常情况下的进气阀间隙和排气阀间隙分别设置为0.65 mm和0.70 mm。
本次试验共采集 4段信号,每段信号的采样时长为20 s,采样频率为20.48 kHz,总共为65 536个点。
2 小波能量谱分析
2.1 小波分析
基于傅立叶变换的FFT频谱分析能有效处理平稳随机信号,然而柴油机的振动信号中包含大量的非平稳信号,所以基于傅立叶变换的频谱分析无法满足要求。
小波分析技术具有良好的时频局部化特性,不仅可以分析平稳的随机信号,还可以分析非平稳的随机信号。因此,小波分析是诊断柴油机振动信号故障的较为理想的工具[8-13]。
2.2 小波原理简介

信号f(t)的积分小波变换为

引入内积
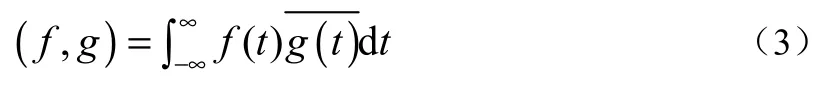
记

如果

则称J(t)为正交小波。
S. Mallat在构造正交小波基的时候提出了多分辨率分析(multi-resolution analysis)的概念,给出了正交小波的构造方法以及正交小波变换的快速算法,即Mallat算法。对于多分辨率分析的理解,以三层分解为例,其小波分解树如图1所示。小波分解将原始信号逐级向下分解。图中 S代表原始信号,A1、A2、A3分别代表第一、二、三层中的低频系数,D1、D2、D3代表对应的高频系数。
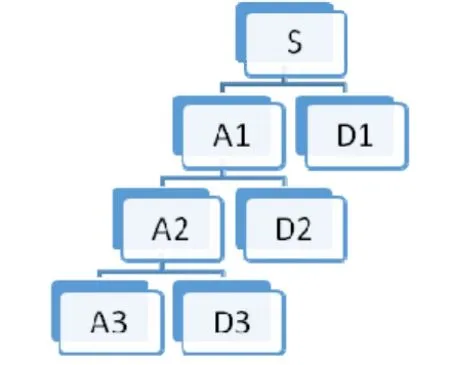
图1 小波分解树
本文利用多分辨率分析进行了故障诊断之前的特征提取。对其中4段信号进行小波分析,将每段信号分为10组,其中每组数据时长为2 s,频率为20.48 kHz,每组数据包含2 000个点。使用db2作为小波基函数,将样本分三层,取出第三层中的低频系数cA3。图2为不同工况和条件下1组信号的小波分析图。

图2 振动信号样本小波分析结果
对提取出的低频系数cA3进行能量频段分析,提取能量特征值。设各个频段的能量为其中:j为层数;N为该频段的采样点数。表2~表5是各个频段的能量和整个信号的能量比例。将结果作为特征构成五维特征向量输入到遗传算法优化的支持向量机中进行分类。在40组数据中分出8组数据构成训练集,剩下的32组数据构成测试集。
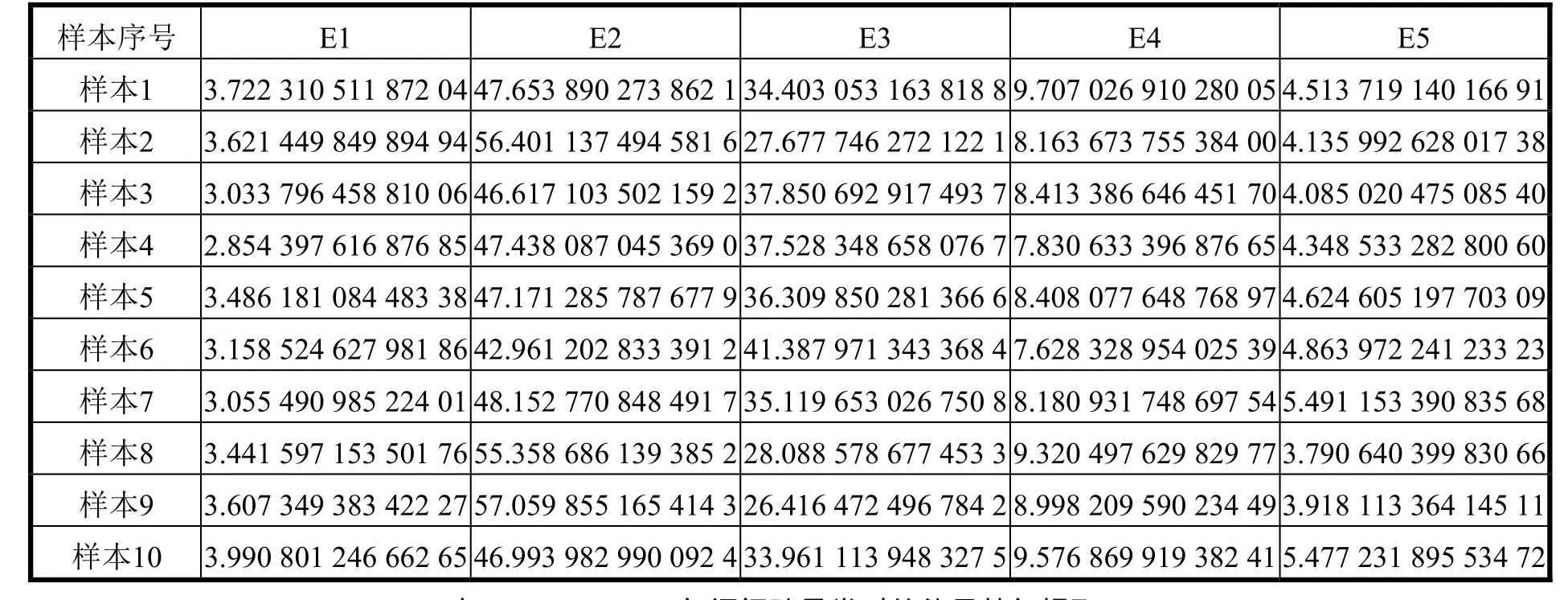
表2 700 r/min,气阀间隙正常时的能量特征提取

表3 700 r/min,气阀间隙异常时的能量特征提取
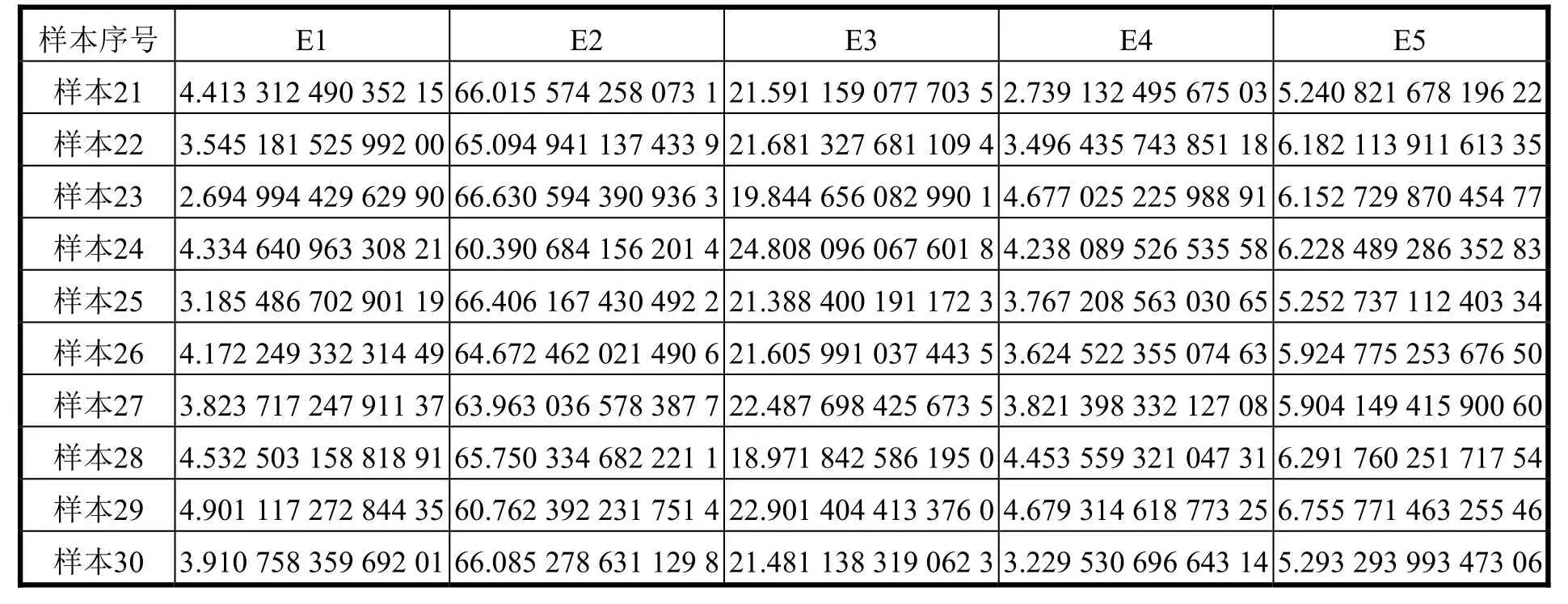
表4 900 r/min,气阀间隙正常时的能量特征提取
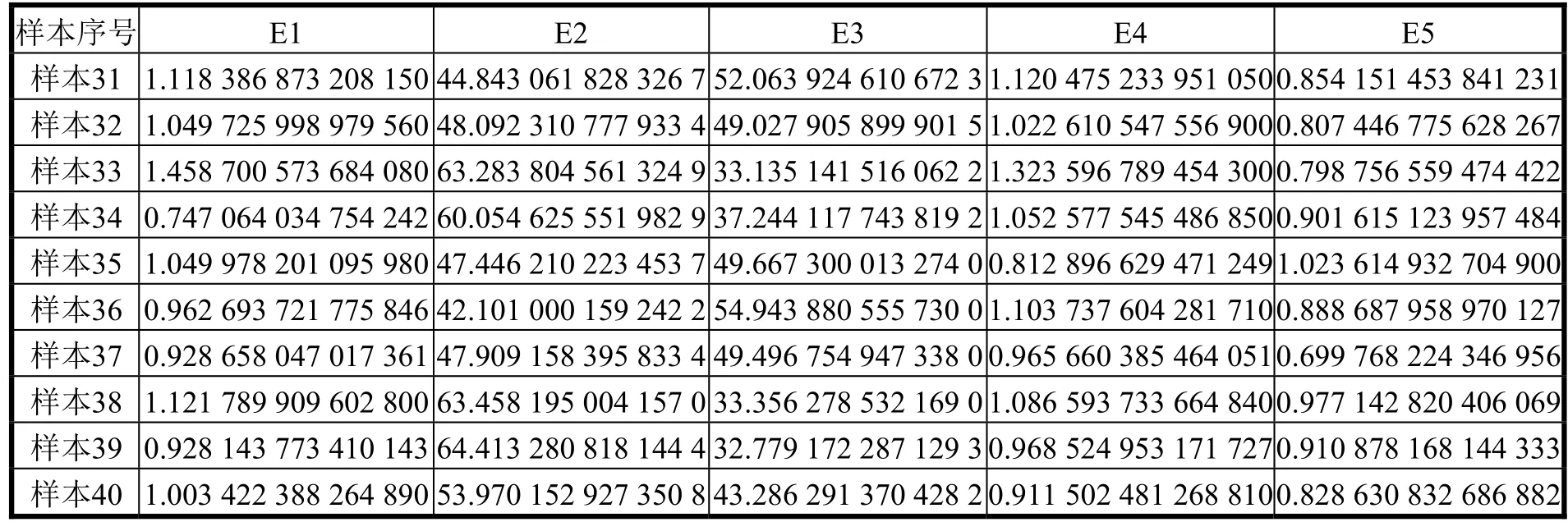
表5 700 r/min,气阀间隙异常时的能量特征提取
3 支持向量机分析
不同于传统的机器学习方法,SVM是建立在统计学习理论基础上的一种新的机器学习方法。传统的机器学习方法遵循经验风险最小的原则,而 SVM 是根据结构风险最小化原则所提出的。与人工神经网络相比,SVM具有更强的推广能力。
以二分类为例,假设SVM在训练阶段的输入向量为n、维向量为x,SVM输出为−1或1,即训练样本数据集为(xi; yj),其中通过一个非线性映射 ϕ,把样本空间映射到一个高维乃至无穷维的特征空间中,在特征空间内构建一个超平面,该超平面可以表示成

所有的训练样本满足如下条件


式中:C为用于平衡松弛变量i和分类边界的惩罚参数。
式(8)的解为
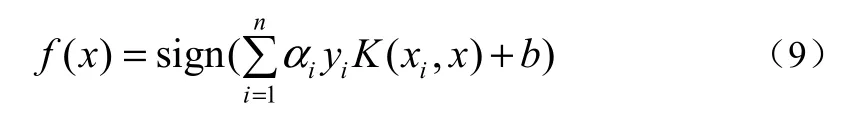
式中:K为SVM的核函数。径向基是应用广泛的核函数,该函数有两个参数:惩罚因子 C和核函数参数σ,其表达式为

由于径向基核函数的参数C和σ的选取没有理论基础,而它们的取值会直接决定SVM分类器性能的优劣。为了能够找到C和σ的最优值,将GA算法应用到SVM的参数寻优中。GA_SVM的算法框图如图3所示。
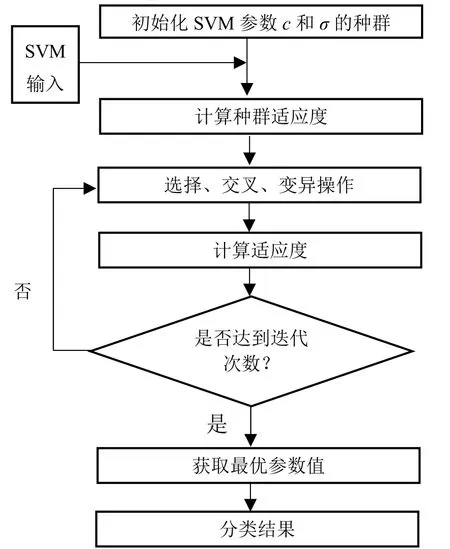
图3 GA_SVM算法图
将4组数据每中每组10个样本随机抽取2个样本作为训练集输入SVM模型进行训练,得到一个训练后的SVM模型。训练集数据如表6所示。

表6 SVM训练样本
平行坐标是对多维空间的两维表示,是表示多维数据及进一步分析其相互关系的重要可视化技术[14]。训练后的SVM模型平行坐标图如图4所示。将剩下的每组8个样本,共32个样本作为测试集输入到SVM模型中进行分类,最终测试结果如表7所示,支持向量机正确分类的准确率为100%。

图4 训练后的SVM平行坐标图
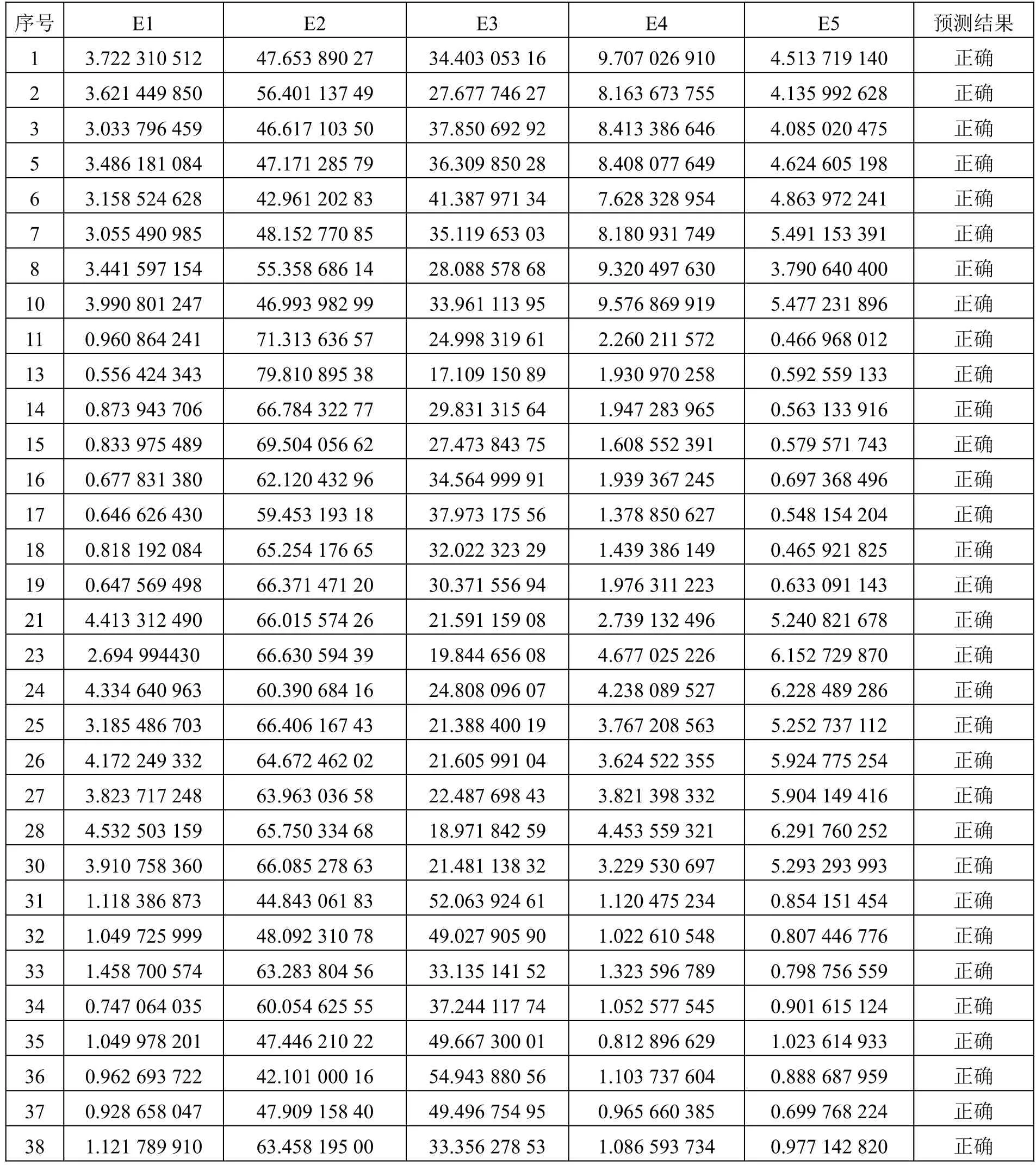
表7 SVM测试集结果
4 结束语
本文利用小波分析对数据进行降噪,再利用小波能量谱分析对数据进行特征提取,将提取出的特征向量输入到遗传算法优化的支持向量机中建立 SVM 模型,最后利用 SVM 模型对数据进行分类。该方法对本次试验的40组数据分类的准确率可以达到100%,说明该方法快速有效,能对柴油机气阀间隙的故障进行准确的分类,特别是能在不同工况下对柴油机气阀间隙的异常做到准确的分类。本方法在其他机械故障诊断中也具有相当重要的参考价值。

