向量视角下的三角形面积公式及运用

四川省内江师范学院数学与信息科学学院 (641100) 王昌林 许凤姣 刘成龙

众所周知，由两边及夹角可以确定一个三角形.因此，从向量的角度看，两个共点的向量可以确定一个三角形.进而由两个共点的向量可以表示所确定三角形的面积.[1]本文给出向量视角下三角形面积的两个公式及运用.

一、向量视角下的三角形面积公式

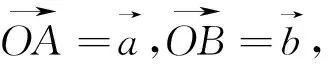
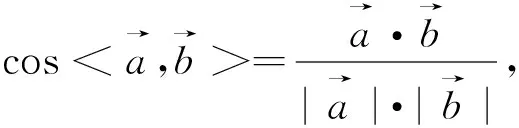
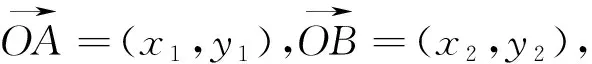
图1

为便于进一步给出面积公式的表征形式，先引入向量积的概念，如下：

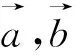
二、公式的应用

高考向量部分对三角形面积的考查主要有两个方面：直接求三角形的面积；四边形面积问题可转化为三角形面积来处理.[1]下文介绍三个公式在高考解题中的应用.

例1 (2018年全国Ⅲ卷理科第6题)直线x+y+2=0，分别与x轴，y轴交于A，B两点，点P在圆(x-2)2+y2=2上，则ΔABP面积的取值范围是( ).

A.[2,6]B.[4,8]

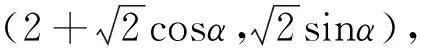
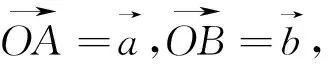
评注：例3即是公式一，选C.

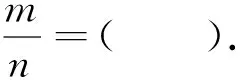
评注：例2将平行四边形的面积转化为两个面积相等的三角形，借助公式二即可得到问题的解.

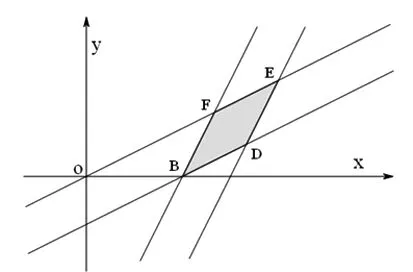
图2

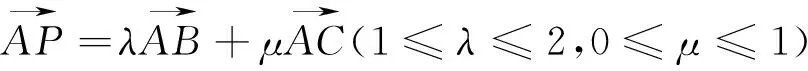
图3

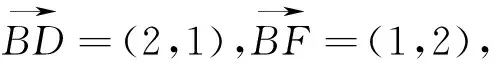
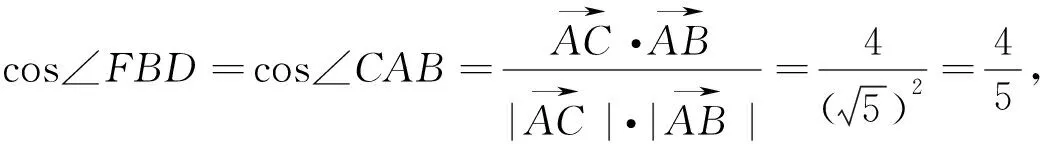
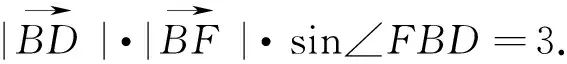
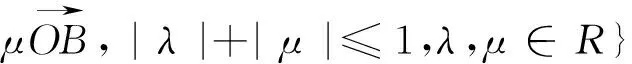
图4

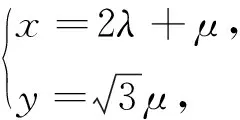
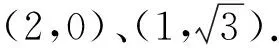
例8 (2017年全国Ⅰ卷文科18题)在四棱锥P-ABCD中，AB∥CD，且∠BAP=∠CDP=90°.

(Ⅰ)证明：平面PAB⊥平面PAD；

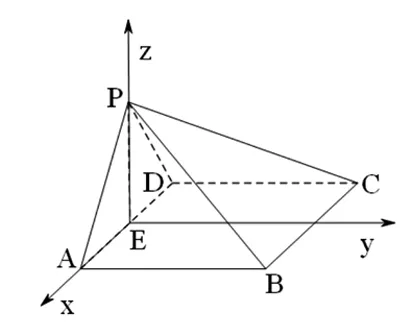
图5

解:(Ⅰ)略；