一道征解题的探究

安徽省安庆市大别山科技学校 (246600) 胡淑芳安徽省岳西县汤池中学 (246620) 杨续亮

《数学通讯》(上半月)刊“问题征解”栏目，每期精选5道试题进行征解，隔一期展示部分优秀解答，这些试题具有新颖、有趣、实用、灵巧，富有启发性的特点，能够启迪学生思维，开发学生智力，深受广大师生的欢迎.本文选取其中一道试题进行探究.

一、征解题的证明

不妨设b介于a,c，则(b-a)(b-c)≤0,即b2-(a+c)b+ac≤0.

而由绝对值不等式可得|a-b|+|b-c|+|c-a|≥|a-b+b-c|+|c-a|=2(a-c),

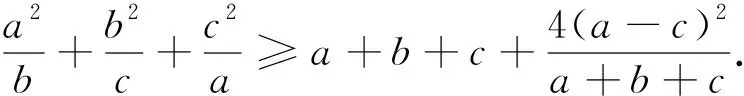
此结论要强于征解题，右端的项(a-c)2也可以换成(a-b)2或(b-c)2，同时可以得到

2005年巴尔干数学奥林匹克试题：

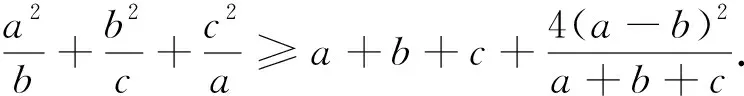
下面对这一结论做些推广.

二、征解题的推广

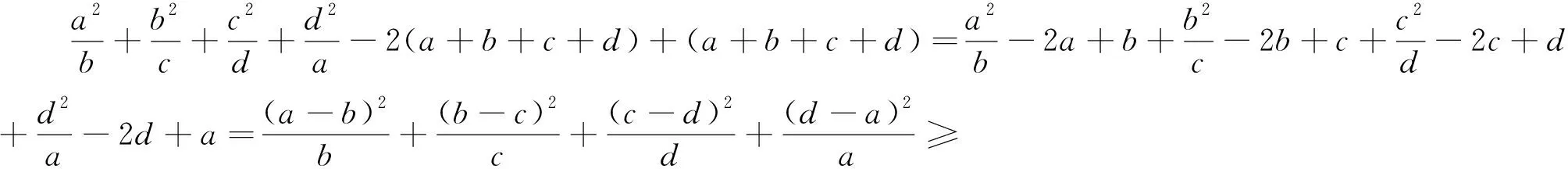
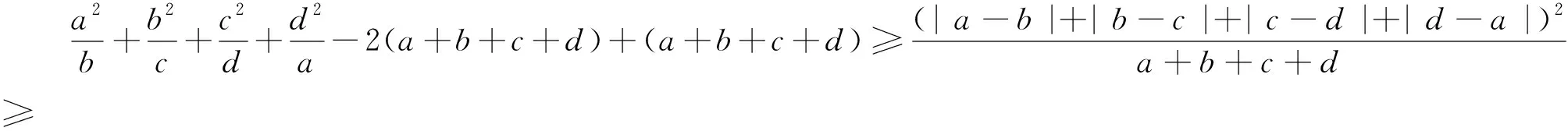
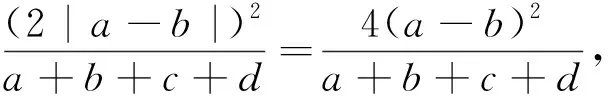
评注：安振平老师在《数学通讯》2006年第9期《一道巴尔千数学奥林匹克竞赛试题的推广》中给出了证明.本题还可以进一步弱化得到1984年高中数学联赛试题：

针对指数可以作如下推广

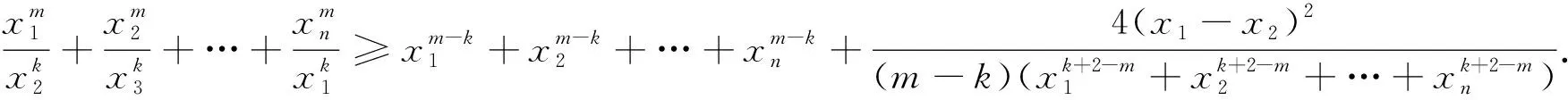
注：当m=2,k=1为推广2.当m=2,k=1,n=3为2005年巴尔干数学奥林匹克试题.

而对分母增加元数进行推广可以得到：

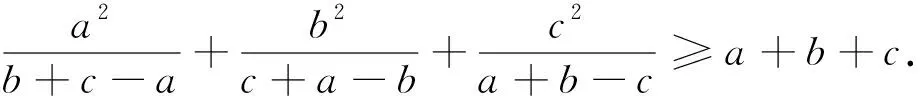
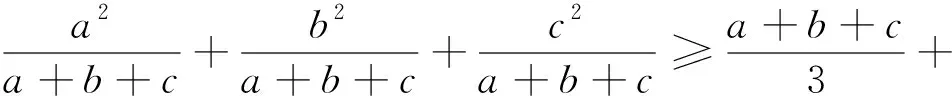
以上三个推广可以形成统一的形式：

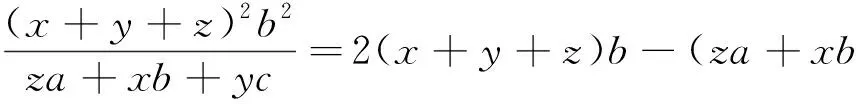
由二元权方和不等式可得

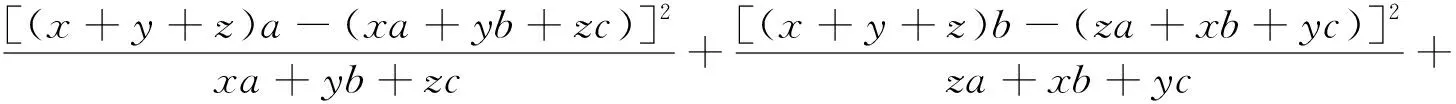
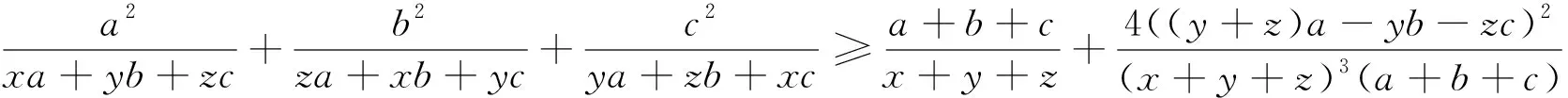
针对335号证解题有如下推广

更有一般性的命题结论：

请有兴趣的读者给出以上不等式的证明.