考虑刚柔耦合特性的SUV控制臂强度分析

赵 燕，赵 攀，阮成明，王小康

1 引言

悬架系统是现代汽车上的重要总成之一，直接影响到汽车操纵稳定性和平顺性，控制臂在悬架中起导向和支撑的作用，同时将外界作用在车轮上的激振力传递给车身[1]。控制臂的工作条件复杂，其机械性能要求严格，因此校核控制臂的强度，研究其可能出现的问题，对于整车的设计与开发具有非常重要的理论意义与实践价值。

对控制臂进行强度分析的难点在于载荷和边界条件的施加[2]。在载荷计算方面迄今没有基本的计算准则，汽车制造企业仍按照自身经验设计，遵循企业标准选取了4种典型极限工况并计算了对应的轮胎接地力，利用刚柔耦合动力学模型准确求解了控制臂输入载荷；在边界条件施加方面，汽车行驶过程中控制臂处于动平衡状态，在模型上施加正确合理的边界较为困难，建立真正的自平衡力系难以实现，故应用惯性释放法进行了控制臂的强度分析，使分析结果与实际更加符合[3-4]。

2 控制臂有限元模型的建立

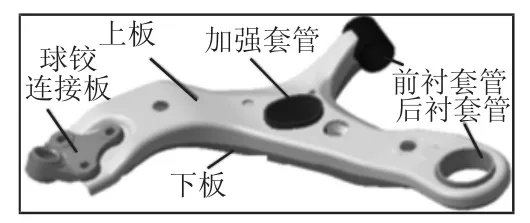
图1 控制臂结构Fig.1 Structure of the Control Arm

表1 材料力学参数Tab.1 Mechanical Parameters

按照企业提供的控制臂CATIA数模，如图1所示。该控制臂为双层冲压件，上下两薄壁板焊接相连，球铰座连接板与两薄壁板通过螺栓连接，前后衬套管与加强套管均焊接于薄壁板上。控制臂所使用的材料为宝钢生产的SAPH440和35#，其材料力学参数，如表1所示。

运用HyperMesh进行网格划分时，将上下两薄壁板抽取中面，采用壳单元对其进行网格划分；前后衬套管因为是圆筒状比较规则，采用六面体网格进行划分，球铰连接板形状复杂采用四面体单元划分。划分网格完毕后，焊接位置采用Seam方式创建焊缝，螺栓连接处采用Beam梁单元进行处理。实车中控制臂与副车架通过两个衬套连接，与转向节采用球铰连接，在建立有限元模型时，在前后衬套管及球铰座中心采用Rbe2蜘蛛网状单元处理，最后建立的控制臂有限元模型，如图2所示。

图2 控制臂有限元模型Fig.2 Finite Element Model of the Control Arm

3 麦弗逊刚柔耦合动力学模型的建立

3.1 控制臂柔性体的生成

在多刚体动力学中如果考虑部件变形建立的动力学模型称为为多柔体系统。由于汽车在行驶过程中控制臂受力情况复杂，在建立动力学模型时应将控制臂视为柔性体处理，即将控制臂的模态信息导入多体动力学模型，建立刚柔耦合模型[5]。

利用Hypermesh中生成的控制臂有限元模型，在MSC.Patran中定义外接点和超单元，导入MSC.Nastran计算得到模态中性文件。由于柔性体导入Adams时，柔性体自由度数目巨大，所以在利用Nastran计算生成模态中性文件时运用模态综合（CMS）法缩减模型自由度[6]，但同时也会带来模态计算误差。在Hypermesh中自由模态分析得到的前12阶模态频率和在Adams中检查模态中性文件获取的频率，如表2所示。

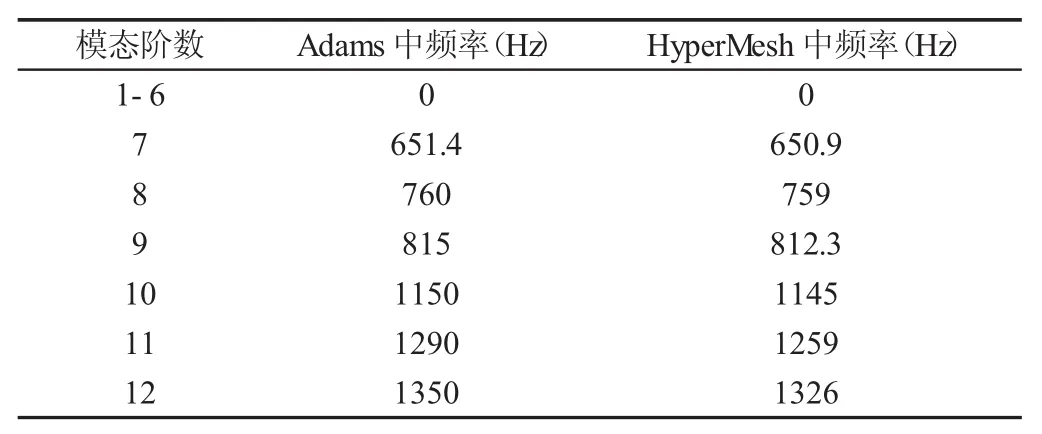
表2 HyperMesh与Adams中频率对比Tab.2 HyperMesh and Adams Frequency Comparison

由表2可知，在Adams中检查模态中性文件的频率与有限元软件中得到的频率误差在5%以内，说明得到的控制臂柔性体文件基本正确。

3.2 建立刚柔耦合麦弗逊前悬架模型

这里涉及的前悬架系统为麦弗逊独立悬架，主体部分由前支柱总成和控制臂组成，汽车行驶过程中侧向力大部分由控制臂承受，而车轮上下跳动时的垂向力则由前支柱承受。SUV车麦弗逊前悬参数，如表3所示。

根据表3中参数，将控制臂柔性体导入Adams/car中后，组成的麦弗逊悬架刚柔耦合动力学模型，如图3所示。

表3 SUV汽车前悬参数Tab.3 Front Suspension Parameters of the SUV Car

3.3 悬架模型正确性验证

建立悬架模型后，须对其进行正确性验证。一般验证方法是通过分析模型的运动学特性与实车测试数据进行比对，如果如果误差在一定范围内说明建立的悬架模型与真实的悬架系统较为接近，即悬架模型是有效的。

车轮同向平行跳动可以模拟汽车在各种工况下悬架的运动状态[7]。通过车轮同向平行跳动仿真，得到悬架各性能参数随轮跳的变化情况，这些参数正是评价悬架运动规律有效性的指标。因此在Adams/car中对麦弗逊悬架进行了（-80～80）mm的车轮同向平行跳动仿真，并与企业提供的实车K&C测试数据进行了比对。企业SUV车K&C测试试验台，如图4所示。

图4 SUV车K&C试验台Fig.4 K&C Test Rig of the SUV Car

3.3.1 前束角随轮跳变化

车轮前束角是车轮前端向内侧倾斜的夹角。前束角能够平衡外倾角带来的车轮外滚的趋势，减少轮胎磨损，提高轮胎寿命。车轮前束角随轮跳变化曲线，如图5所示。

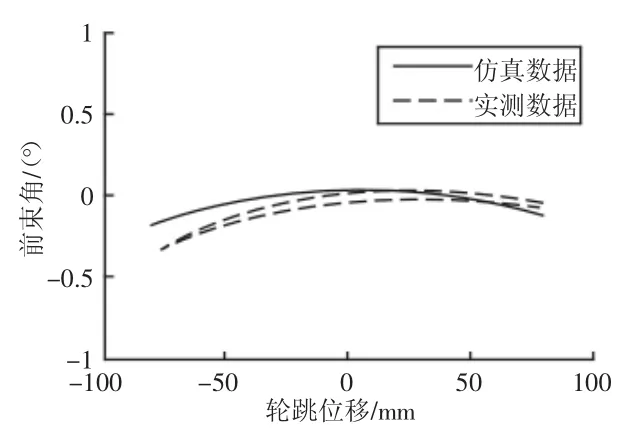
图5 前束角随轮跳变化曲线Fig.5 Toe Angle Changes with the Wheel Travel

从图5可以看到，当轮跳位移为0时，前束角值也在零附近，这可以保证汽车在较平路面行驶时的直行稳定性。仿真的前束角在车轮上跳过程中向负值方向变化，这保证了汽车转弯时具有不足转向的特性，操稳性也会随之提高，且仿真数据与实测数据变化趋势趋于一致，满足要求。

3.3.2 外倾角随轮跳变化

外倾角是指车轮端面向外倾斜的夹角。在汽车满载状态下，汽车前轴受载使外倾角减小至零，减小轮胎磨损，汽车转弯时，车轮上跳产生负变化的外倾角，使车轮与地面接触面积尽可能大，使车辆在转弯时拥有较大的侧向力。外倾角随轮跳变化曲线，如图6所示。

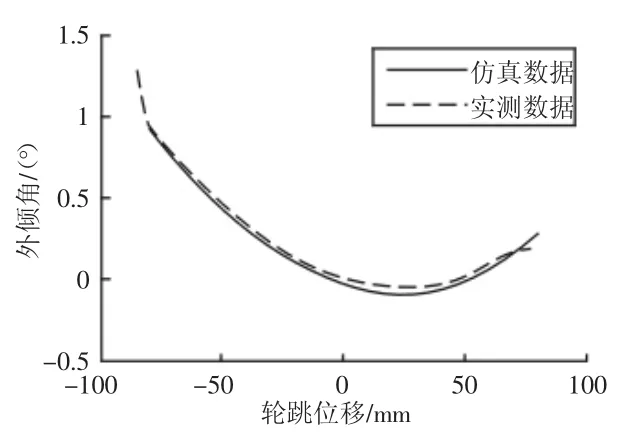
图6 外倾角随轮跳变化曲线Fig.6 Camber Angle Changes with the Wheel Travel

从图6可以看出，车辆设计状态下外倾角处于零值附近，使车轮垂直于路面，同时抵消由于路面不平作用在车轮上的微侧倾力，使车轮具有直行稳定性。图中仿真结果与实测数据基本一致，说明外倾角变化满足要求。

3.3.3 侧倾中心高度随轮跳变化

侧倾中心为汽车侧倾轴线的离地高度。侧倾中心高，侧倾角会变小，舒适感会增强。但较高的侧倾中心高会增大汽车的轮距，加速轮胎的磨损。侧倾中心高度随轮跳变化，如图7所示。

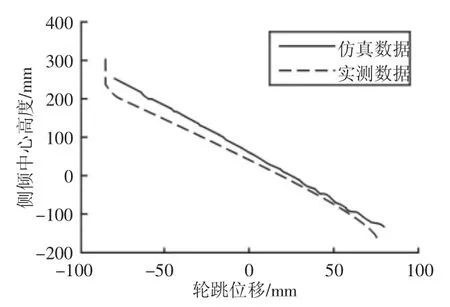
图7 侧倾中心高度随轮跳变化曲线Fig.7 Roll Center Height Changes with the Wheel Travel

从图7中可以看出，侧倾中心高度仿真数据与实测数据变化一致，满足要求。

3.3.4 轮心处垂向力随轮跳变化

从图8可以看出，轮心垂向力在轮跳（-80～70）mm基本近似直线，直线的斜率即代表了悬架整体刚度，在（70～80）mm这段垂向力急剧上升。通过企业所给整车参数可知前悬上行程为72mm，在72mm之后由于上行程限位块开始发挥作用，使得垂向力变化加剧。图中仿真数据与实测数据变化一致，满足要求。

综上所述，建立的麦弗逊悬架刚柔耦合模型仿真参数与企业提供的实车数据基本一致，说明了建立的模型基本正确，可以用来进行下一步的控制臂载荷提取。

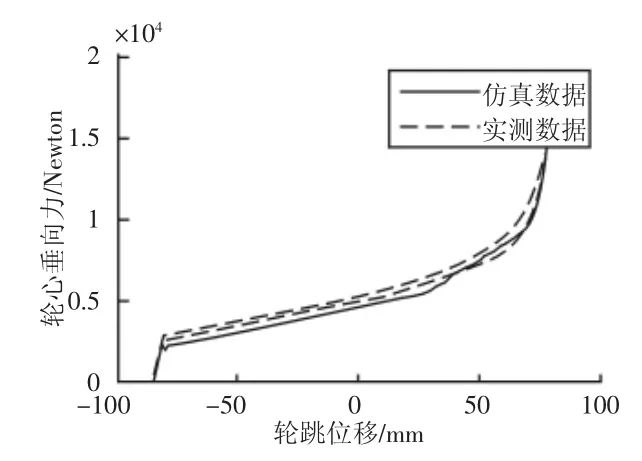
图8 轮心垂向力随轮跳变化曲线Fig.8 Wheel Center Vertical Force Changes with the Wheel Travel

4 控制臂强度分析

4.1 静载荷工况及其说明

根据企业自身设计规范，选取了垂向冲击、角度冲击、直线制动、转弯制动4种典型工况，根据这四种工况可以非常全面的评估悬架性能表现及悬架各零部件机械性能。以整车坐标系为参照，四种典型工况说明如下：

垂向冲击：3g垂向力；

角度冲击：0.7g纵向力，0.6g侧向力，1.8g垂向力；

直线制动：1g纵向力，1g垂向力；

转弯制动：0.8g纵向力，1g侧向力，1g垂向力。

根据四种典型工况下的X，Y，Z向的加速度及企业提供的整车参数，以整车坐标系为参照，计算得到的左前轮轮胎接地力，如表4所示。

有的甚至原本是一价动词，在进入双及物构式后，构式赋予其“接受”的含义，增加接受者和接受物。例（17）是Goldberg提供的一个经典例句：

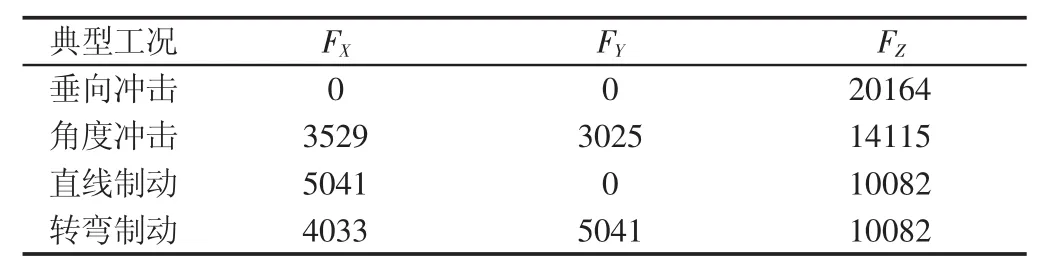
表4 左前轮轮胎接地力Tab.4 Left Front Tire Contact Force

4.2 惯性释放法原理

在汽车行驶过程中，控制臂一直处于动平衡状态，在有限元软件中对控制臂施加静载边界条件十分困难。为了解决这个问题，采用惯性释放法求解控制臂在载荷下的应力结果。

惯性释放法就是采用惯性力与外力构成一个平衡力系，消除外在约束力对应力和应变的影响，从而对结构进行精确的有限元分析。根据有限元构造的静动力平衡方程为：

式中：｛F｝—所有节点外载荷分量；｛δ¨｝—所有节点加速度分量；［M］—质量矩阵。

求解上述方程便得到了节点的加速度量，对结构施加反向的外载荷即可以与惯性力平衡，结构便处于自平衡状态[9-10]。

4.3 计算结果及分析

在ADAMS中对刚柔耦合悬架模型施加表4中所示的轮胎接地力，提取控制臂前点、后点及外点处的载荷。在HyperMesh中对有限元模型施加相应载荷，应用惯性释放法进行静强度分析，得到的控制臂在各典型工况下的应力分布云图，如图9所示。

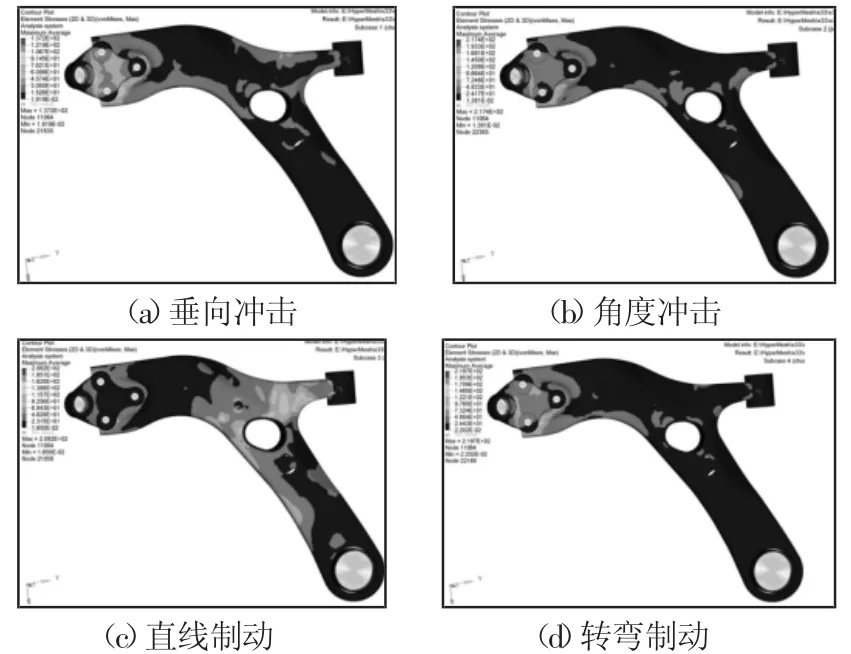
图9 典型工况下控制臂应力分布云图Fig.9 Control Arm Stress Contours of the Typical Conditions

从图9可以看到，该控制臂在4种典型工况下，零件绝大部分位置受力较小，控制臂前衬套座和后衬套座与薄壁板的连接处及其边缘均受力较大，这是由于纵向制动力所引起的，特别是在直线制动工况况下，这种现象更加明显。四种工况下，控制臂的中心区域应力较小，基本不承受载荷，而在球铰座与下板的螺栓连接处均出现了应力集中的现象。这是由于控制臂在水平面弯矩和纵向平面内的扭矩作用下应力分布不均所导致的。

四种典型工况下控制臂的最大应力，如表5所示。

表5 控制臂强度分析结果统计Tab.5 Statistical Analysis of the Control Arm Strength

为了保证零件在实际使用中不发生失效，取安全系数为1.8。控制臂的两种材料的强度极限分别为440MPa和530MPa，所以：

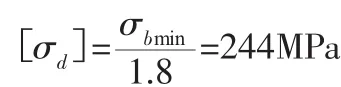
式中：［σd］—许用应力；σbmin—最小极限强度。从表5可知，控制臂最大应力均小于最大许用应力，故控制臂强度满足设计要求。

5 结论

建立了以控制臂为柔性体的麦弗逊刚柔耦合模型并对其正确性进行了验证，针对4种典型工况下的载荷边界条件，计算了了对应的轮胎接地力，并以此为输入进行了悬架模型的静载仿真精确提取了控制臂的载荷输入。应用惯性释放法对控制臂进行了强度分析，在保证精度的前提下提高了计算效率，结果表明控制臂强度满足设计要求。