第二类Wiener-Hopf积分方程的复合Nyström-Clenshaw-Curtis方法

郭魏丽，林福荣

（汕头大学数学系，广东 汕头 515063）

0 引言

本文考虑第二类Wiener-Hopf积分方程的高精度快速解法，这是一类定义在正半轴上的卷积方程：

其中 k（t－s）是核函数，f（t）为已知函数，u（t）是待求函数.这类方程有广泛的应用背景[1]145-146，186-189，其数值方法吸引了众多学者[2-5].

Wiener-Hopf积分方程的数值解法可分为两类.一类是对半无限区间进行截断，化为求解有限区间上的积分方程.截断方程的形式如下[3-5].

Gohberg等提出应用预处理共轭梯度法求解该方程，并引进循环预处理算子提高算法的效率[3].Lin等则提出用卷积算子作为逆预处理算子[5].Kang等提出Nyström-Clenshaw-Curtis（NCC）求积方法，并应用于方程（2）的离散[4].NCC方法是求解具有半光滑核函数的积分方程的高精度方法，但离散矩阵没有结构，而且稳定性也存在问题.Chen等提出了修正的NCC求积方法，使得NCC求积方法更加稳定[6].另一类数值解法则不作截断，直接对方程（1）进行离散[2，7].

本文在NCC方法的基础上，提出复合NCC求积公式，并对离散方程组做适当的处理，使得系数矩阵有Toeplitz块结构.然后引进循环块矩阵作为预处理矩阵提高预处理迭代方法的收敛速度.

本文余下部分安排如下.第2节介绍NCC方法及其主要性质，第3节讨论用复合NCC方法离散Wiener-Hopf的截断方程（2），第4节考虑离散方程组的快速解法，第5节给出若干例子说明本文提出的算法的有效性.

1 Nyström-Clenshaw-Curtis求积方法

先介绍Chebyshev网格上的插值函数的逼近性质.设Tj（s）＝cos（j arccos（s）），j＝0，1，2，…，是一列 Chebyshev 多项式，

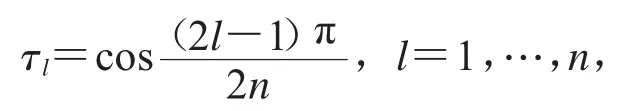
是n次Chebyshev多项式Tn（s）＝cos（n arccos（s））的根.

引理1.1（Jackson第五定理[8]95-96）设h∈C[－1，1]且存在正整数k使得h的k阶导数h(k)连续.用表示用Qn表示次数不超过（n－1）次的多项式的集合.设（Bnh）（x）是 h（x）的最佳逼近多项式，即

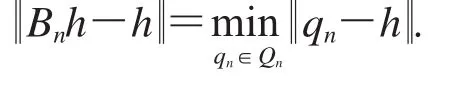
则当n≥k时，有

Lebesgue函数和Lebesgue常数是分析插值多项式的误差的有用工具.对于一个给定的插值网格{s1，…，sn}，Lebesgue函数定义为

是第k个Lagrange插值基函数，Lebesgue常数定义为对于Chebyshev网格有用（Tnh）（s）表示 h（s）在 Chebyshev网格上的插值多项式

下面引理给出（Tnh）（s）的误差估计[9].

引理 1.2 设 k 为正整数，h（s）∈Ck[－1，1].如果 n＞k，则

可见，用Chebyshev网格对光滑函数进行插值非常有效.

下面介绍NCC求积方法.考虑积分方程

其中右端函数 g（t）和未知函数 x（t）是光滑函数，h（t，s）是一个 p－半光滑核函数（p 为正整数），即

其中hi（t，s）∈Cp（[－1，1]×[－1，1]），i＝1，2.注意到

由于h1（t，s）和h2（t，s）在[－1，1]×[－1，1]中光滑，h1（t，s）x（s）和h2（t，s）x（s）也在[－1，1]×[－1，1]光滑.NCC求积方法的关键点是对固定的t，把（4）中的被积函数看作s的函数，在整个区间[－1，1]进行有效逼近.

定义

其中系数 αl，j由插值条件

确定，即

上式中

于是

经计算得

则由（7）和（8）可得

由（5），（6），（11），（12）得

其中W＝CSLC－1，

类似地，设

其中S由（9）给出，

由（13）和（14）可得（3）的 NCC离散方程组

说明：（1）对于一般区间[a，b]上的积分方程

可以通过简单的仿射变换化为[-1，1]上的积分方程：

（2）设h1（t，s）x（s）∈Cp（[－1，1]2），h2（t，s）x（s）∈Cq（[－1，1]2），则当NCC方法用于（15）时，数值解有如下的误差界：其中 c 为正常数，r＝min（p，q）.

2 求解第二类Wiener-Hopf积分方程的NCC方法

考虑截断Wiener-Hopf积分方程（2）的离散.必须指出，当积分区间比较大时，直接应用NCC方法可能导致核函数的函数值过大，造成很大的舍入误差.比如像这样的函数，当积分区间较大时用NCC方法得不到高精度的解.复合NCC公式可以作为一种解决方法.其基本思想是对区间进行合理的分段，然后在每个小区间上应用NCC方法，从而避免出现较大的舍入误差的现象.通过分析我们发现：如果把区间[0，T]划分为等长的子区间，应用复合NCC公式并将求积节点作适当的重排，则系数矩阵具有Toeplitz块结构.这样可以由Toeplitz块结构和循环块结构设计快速算法，显著减少计算量.

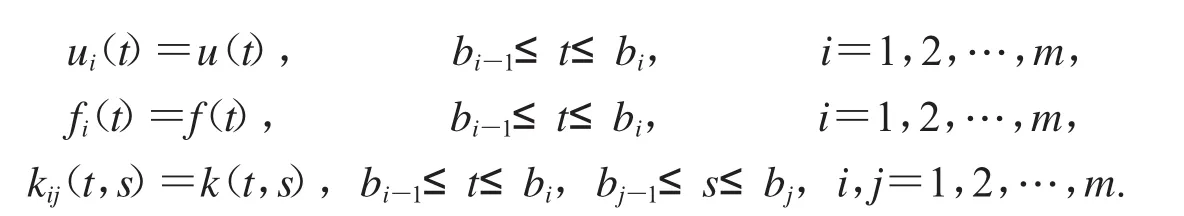
积分方程（2）可以写成如下积分方程组：

考虑在每个小区间[bj－1，bj]，j＝1，2，…，m，应用NCC求积公式，每个小区间都取n个节点.令

则（16）的离散方程为

定义如下的mn维向量f和u：

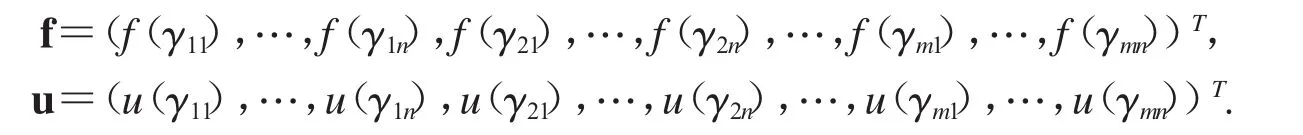
设A为m×m分块矩阵

其中 Aij为 n×n 矩阵，其（k，l）元素为

上述方程组可以写成如下紧凑格式：

当mn很大时，用直接法求解离散方程组的计算量很大.因此，我们考虑用迭代法求解，以提高解方程的效率.

3 离散方程组的预处理迭代解法

由（18）定义的分块矩阵没有特殊的结构.经过研究，我们发现对求积节点作适当重排后，系数矩阵具有Toeplitz块结构.由此我们得到求解线性方程组（17）的快速算法.文献[10]研究了核函数光滑的情形.如果 Tn＝[ti，j]n×n满足 ti，j＝ti－j，则称 Tn是一个 n 阶Toeplitz 矩阵.特别地，如果 Cn＝[ci－j]n×n满足 ci＝ci－n，i＝1，2，…，n－1，则称 cn是一个 n阶循环矩阵.循环矩阵可由傅里叶矩阵对角化：

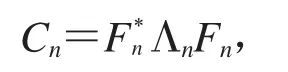
则方程组（17）化为

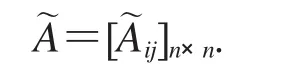
其中Λij为对角阵（其对角元由的第一列经快速傅里叶变换得到），有

其中P是一个mn×mn的置换矩阵，Dk是n×n的矩阵，满足

由于线性方程组（19）的系数矩阵可能不是对称正定的，我们考虑对其法方程组应用共轭梯度法（CGNR）和预处理共轭梯度法（PCGNR）.记则（19）的法方程组为

其中B*表示B的转置.

取预处理矩阵为Q＝M*M，用PCGNR方法求解下列方程组

为完整起见，我们给出求解（20）的PCGNR方法（如果Q改为单位矩阵，则为CGNR方法）.

应用PCGNR方法求解线性方程组（20）的每步迭代的主要工作是计算和求解下面简要说明快速算法的步骤：

因此，在求解这类积分方程时，我们可以选取不太大的n（如n＝16），这样，每步迭代的计算量比较小.

4 数值例子

本节给出数值例子说明本文提出的方法的有效性.在CGNR和PCGNR方法中，初始解为零向量，终止条件为剩余向量的相对误差小于10－14，即∈＝10－14.所有的计算在Dell Optiplex 9020台式计算机上用Matlab运行.在下面的表格中，“误差”表示数值解的相对误差，即其中分别表示数值解和精确解；分别表示高斯消去法，CGNR方法（矩阵-向量相乘用快速算法），CGNR方法（矩阵-向量相乘不用快速算法），PCGNR方法的计算时间，单位为秒；ICGNR，IPCGNR分别表示两种方法的迭代次数.

例4.1.考虑

取T＝80，n＝16，相关的结果如表1所示.从表1可以看出：（1）PCGNR方法的收敛比CGNR方法快得多，但在计算时间方面并没有优势.主要原因在于构造预处理矩阵需要较多的时间.（2）随着m的增大，数值解的精度提高非常快.（3）当m较小时，快速算法的优势不明显；随着m增大，快速算法的优势越来越大，如m＝128时，TCGNR约为的1/9，为TGE的1/7.

表1 误差、计算时间和迭代次数（例题4.1）

例4.2.考虑

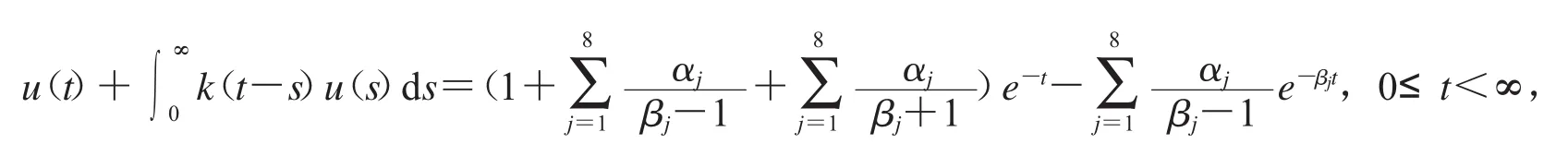
取T＝80，n＝16，相关的结果如表2所示.我们看到与例题4.1类似的结果：（1）PCGNR方法的收敛比CGNR方法快得多，但在计算时间方面并没有优势.（2）随着m的增大，数值解的精度提高非常快.（3）当m较小时，快速算法的优势不明显；随着m增大，快速算法的优势越来越大.

表2 误差、计算时间和迭代次数（例题4.2）

从以上的数值结果我们看到：复合NCC方法是一个精度非常高的方法，这与理论结果相符；利用矩阵的Toeplitz块结构，快速矩阵-向量乘法可以提高算法的效率；引进预处理矩阵虽然能加快迭代方法的收敛速度，但在计算时间方面没有优势.如何更加高效的预处理矩阵，是一个值得进一步研究的问题.